Числовая обработка результатов лабораторного эксперимента
Методы измерений
Всякая лабораторная работа - это эксперимент, при котором производится измерение той или иной величины. Если производят измерение, непосредственно сравнивая неизвестную величину с эталоном, то это будет метод непосредственного измерения. Например, измеряя длину стержня, вы сравниваете ее с эталоном – измерительной линейкой. Если непосредственно измерить величину не удается, то измерив какие-либо иные величины, связанные с неизвестной теми или иными законами, можно вычислить эту неизвестную величину. Так для того чтобы узнать величину сопротивления резистора измеряют силу тока I и напряжения U и по закону Ома (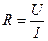
) вычисляют сопротивление R.
Выделяют так же нулевой метод – метод, при котором влияние измеряемой величины компенсируют влиянием подобной же, но действующей в противоположном направлении. Этот метод используется при взвешивании тела с помощью разновесов: вес взвешиваемого тела компенсируется весом разновесов, так что общее действия тела и гирь на коромысло весов будет равняться нулю.
Ошибки измерений
Точно определить какую-либо измеряемую величину не возможно. Допустим, необходимо измерить некую величину A. Точное значение нам неизвестно, но в результате n измерений этой величины мы получим ряд значений a1,a2… an, отличающихся от A на ∆a:
(1)
называемые случайными ошибками измерений.
Сложив отдельно правые и левые части этих уравнений получим:
, или 
. (2)
Из теории вероятностей следует, что ошибки измерения лежат в пределах от −∆a до + ∆a. Отсюда можно предположить, что половина всех ошибок будет ∆a иметь положительную величину, а половина отрицательную. Тогда можно сумму всех ошибок приравнять нулю, т.е.: 
, тогда уравнение (2) примет вид:
, (3), отсюда: 
. (4)
Следовательно, за значение измеряемой величины можно принять среднее арифметическое a0 из всех n измерений. Тогда равенство (1) примет вид:
(5)
где ∆a1,∆a2…∆an ошибки отдельных измерений.
Проводя эксперимент, во внимание принимается лишь абсолютное значение этих ошибок. Поэтому вычисляется величина средней арифметической ошибки среднего результата a0: 
. (6)
Если число экспериментов велико, то вычисляют среднюю квадратичную ошибку средней арифметической величины a0: 
. (7)
Окончательный результат запишется в виде: 
. (8)
Если число экспериментов не велико, что будет наблюдаться в большинстве случаев этого лабораторного практикума, то окончательный результат измерений можно записать в виде: 
. (9)
Величина α или ε показывает, насколько истинное значение A измеряемой величины отличается от a0, которую мы принимаем за A.
Абсолютная ошибка не дает представлений о точности эксперимента. Для определения точности используют относительную погрешность измерения средней арифметической величины. Она определяется как отношение средней арифметической ошибки к величине средней арифметической всех экспериментов. Чаще ее выражают в процентах: 
. (10)
Ошибки при косвенных измерениях
Предположим некую измеряемую величину A, которая является функцией (A=f(a,b)) нескольких измеряемых во время опыта величин a, b. Как влияют ошибки измерения величин a, b на точность определения величины А? Пусть абсолютные значения погрешностей измеряемых величин a, b равны соответственно ∆a, ∆b. Тогда для различных функций зависимости A от измеряемых величин a, b ошибка рассчитывается различным способом (таблица 1).
Таблица 1
| Действие | абсолютная ошибка ∆А | относительная ошибка ∆А/А |
| A=a+b, A=a−b | 
| 
|
| A=a·b | 
| 
|
| A=an | 
| 
|
| 
| 
|
| 
|
|
ЛАБОРАТОРНАЯ РАБОТА № 1
