Различают силы инерции, вызванные пусками и торможениями механизмов крана; возникающие при неравномерном движении элементов стрелового устройства при установившейся частоте вращения двигателей или при изменении частоты вращения в результате колебаний величины нагрузки (двигатели с мягкой характеристикой); при вращений элементов (центробежные силы инерции) и совместной работе механизмов поворота и изменения вылета (кориолисовы силы инерции); вызванные толчками из-за неровностей путей передвижения; при наезде на концевые упоры (буферы); вызванные качкой плавучих сооружений.
В результате взаимодействия сил инерции и сил упругости элементов механизмов и металлических конструкций возникают динамические нагрузки. Они определяются путем анализа процессов в соответствующей динамической системе, обычно описываемых дифференциальными уравнениями; при этом могут быть учтены многие факторы (зазоры в передачах, нелинейности в упругих связях, затухание колебаний), которые позволяют достаточно точно отразить процессы, реально протекающие при работе крана. При эскизном, а часто и рабочем проектировании для определения динамических нагрузок применяются упрощенные формулы, полученные при решении дифференциальных уравнений движения, или используют силы инерции Fи = ma, где m ~ масса элемента крана, движущаяся с ускорением а.
При составлении уравнений движения могут использоваться как силовые, так и кинематические воздействия. Если на массу m, подвешенную на упругой связи с коэффициентом жесткости с, действует изменяющаяся по произвольному закону сила F(t), то дифференциальное уравнение движения имеет вид

где у — перемещение, отсчитываемое от положения равновесия при отсутствии внешней силы.
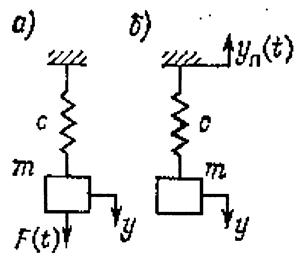
Рисунок 3.1 - Схемы силового (а) и кинематического (в) воздействия
При кинематическом перемещении точки закрепления упругой связи по закону уп(t) дифференциальное уравнение движения массы m:
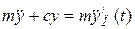
где у — перемещение массы т относительно точки закрепления упругой связи.
Уравнение совпадает по виду с уравнением движения, поэтому все выводы, получаемые при исследовании движения массы m под действием приложенной к ней вынуждающей силы F(t), можно применить и при исследовании движения, вызываемого перемещением точки крепления упругой связи.
При нулевых начальных условиях решение уравнения:

где  — частота собственных колебаний груза,
— частота собственных колебаний груза,  . В выражении t1 следует рассматривать как постоянную величину.
. В выражении t1 следует рассматривать как постоянную величину.
Если на массу m действует ограниченная линейно возрастающая нагрузка, то
 ,
,
где  — статическое смещение массы m под действием силы
— статическое смещение массы m под действием силы  ; Т – время нарастания нагрузки.
; Т – время нарастания нагрузки.
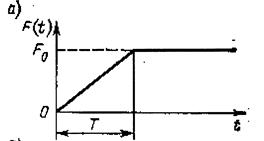

Рисунок 3.2 - Зависимости силового воздействия (а)
и соответствующего ему перемещения массы (б) от времени
Наибольшее значение перемещения
 ,
,
где  — период собственных колебаний груза,
— период собственных колебаний груза,  . Динамический коэффициент
. Динамический коэффициент  как отношение максимального перемещения
как отношение максимального перемещения  к статическому
к статическому  :
:
 ,
,
где  – коэффициент нарастания нагрузки, график изменения которого в зависимости от отношения
– коэффициент нарастания нагрузки, график изменения которого в зависимости от отношения  изображен на рис.штриховой линией. Для практического применения
изображен на рис.штриховой линией. Для практического применения  принимается при
принимается при  по огибающей кривой (сплошная линия). При Т = 0 (мгновенное приложение нагрузки)
по огибающей кривой (сплошная линия). При Т = 0 (мгновенное приложение нагрузки)  ; при
; при 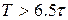
 и с точностью до 5 % динамическим влиянием нагрузки на систему можно пренебречь. Для увеличения времени нарастания нагрузки в передаточные звенья механизмов вводят упругие элементы.
и с точностью до 5 % динамическим влиянием нагрузки на систему можно пренебречь. Для увеличения времени нарастания нагрузки в передаточные звенья механизмов вводят упругие элементы.
В случае мгновенного приложения нагрузки  и времени ее действия tH в соответствии с формулой получим при
и времени ее действия tH в соответствии с формулой получим при  , что
, что  и
и  при
при  . При
. При 
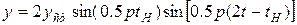 максимальное смещение
максимальное смещение
 .
.
Динамический коэффициент  при
при  , при
, при 
 , при
, при  динамическое перемещение массы m не достигает ycт.
динамическое перемещение массы m не достигает ycт.
В случае внезапного снятия постоянной нагрузки 
Все зависимости, касающиеся сил F(t), действительны также и для крутящих моментов М(t). Динамические нагрузки учитываются с помощью динамических коэффициентов и рассматриваются как квазистатические.
В процессе колебания крановой конструкции и груза происходит их затухание. На интенсивность рассеивания энергии при колебаниях влияет множество факторов; обычно надежной информацией о распределении сил трения не располагают, поэтому оценивают лишь интегральный эффект, например логарифмический декремент колебания.

Рисунок 3.3 - Зависимость коэффициента нарастания нагрузки  от
от 

Рисунок 3.4 - Схема внезапного приложения нагрузки (а)
и соответствующее ей перемещение массы при  (б)
(б)
Логарифмический декремент колебания  определяется как логарифм отношения двух последовательных отклонений:
определяется как логарифм отношения двух последовательных отклонений:  . При расчетах динамических нагрузок в крановых конструкциях он обычно принимается не зависящим от величины отклонения и определяется из экспериментальной осциллограммы затухающих колебаний по выражению
. При расчетах динамических нагрузок в крановых конструкциях он обычно принимается не зависящим от величины отклонения и определяется из экспериментальной осциллограммы затухающих колебаний по выражению
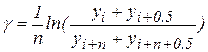 ,
,
где  и
и  — размахи колебаний соответственно в i-м и отстоящем от него на n периодов (i+n)-m циклах колебаний.
— размахи колебаний соответственно в i-м и отстоящем от него на n периодов (i+n)-m циклах колебаний.
Время затухания колебаний от  до отклонения
до отклонения 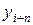
 ,
,
где  — период колебаний системы с демпфированием, при малом демпфировании он практически не отличается от периода колебаний консервативной системы; n — число колебаний при затухании от yi до отклонения yi+n.
— период колебаний системы с демпфированием, при малом демпфировании он практически не отличается от периода колебаний консервативной системы; n — число колебаний при затухании от yi до отклонения yi+n.

Рисунок 3.5 - Развертка затухающих колебаний
Средние значения логарифмического декремента колебаний
| Часть, механизм или узел крана | 
|
| Коробчатые крановые мосты* Металлические конструкции козловых кранов Металлические конструкции стреловых устройств портальных кранов Металлические конструкции портала портальных кранов (включая опорно-поворотное устройство, ходовые тележки я крановые пути) Механизмы подъема груза и поворота портальных кранов Механизмы изменения вылета стрел портальных кранов При крутильных колебаниях груза на канатном подвесе металлургического крана При колебаниях грейфера из плоскости стрелы портального кране | 0.05–0.12 0.10–0.22 0.05 0.35–0.45 0.30–0.50 0.15–0.40 0.04–0.20 0.135 |
*Для крановых мостов с достаточной точностью  ,
где ,
где  — период собственных колебаний моста с тележкой бея груза,
расположенной в середине пролета. — период собственных колебаний моста с тележкой бея груза,
расположенной в середине пролета.
|
Средние значения  для основного тона колебаний приведены в таблице. Допустимое время затухания колебаний конструкции зависит от типа крана и условий его эксплуатации. Если колебания конструкции или кабины крановщика чрезмерны, целесообразно использовать гасители колебаний или виброизоляцию места крановщика.
для основного тона колебаний приведены в таблице. Допустимое время затухания колебаний конструкции зависит от типа крана и условий его эксплуатации. Если колебания конструкции или кабины крановщика чрезмерны, целесообразно использовать гасители колебаний или виброизоляцию места крановщика.
При работе механизма подъема груза динамические нагрузки возникают в периоды неустановившегося движения при подъеме груза с основания и опускании на него; при пуске (торможении) висящего груза на подъем или спуск. При подъеме груза с жесткого основания при слабонатянутом канате (подъем с подхватом) или мгновенном торможении опускающегося груза массой mт динамический коэффициент нагрузки на металлоконструкцию, или отношение максимальной нагрузки Fmax к статической от веса G груза:  может быть определен из рассмотрения двухмассовой расчетной схемы (рис. 3.6, а) по выражению
может быть определен из рассмотрения двухмассовой расчетной схемы (рис. 3.6, а) по выражению
 ,
,
где  — скорость отрыва груза от основания, или скорость его спуска;
— скорость отрыва груза от основания, или скорость его спуска;
 и
и  — приведенные к точке приложения нагрузки соответственно масса и коэффициент жесткости конструкции;
— приведенные к точке приложения нагрузки соответственно масса и коэффициент жесткости конструкции;
 и
и  — частоты собственных колебаний конструкции с грузом:
— частоты собственных колебаний конструкции с грузом:
 ,
,
где знак минус относится к  , знак плюс — к
, знак плюс — к  ,
,  – коэффициент жесткости грузовых канатов;
– коэффициент жесткости грузовых канатов;  — перемещение точки подвеса груза вследствие статического удлинения грузовых канатов от веса груза,
— перемещение точки подвеса груза вследствие статического удлинения грузовых канатов от веса груза,  .
.

Рисунок 3.6 - Расчетные схемы для определений нагрузок на
металлоконструкцию (а) канаты (б) при работе механизма подъема груза
Динамический коэффициент нагрузки на металлоконструкцию крана может быть определен из рассмотрения одномассовой расчетной схемы (рис 20, а при  ) в виде:
) в виде:
 ,
,
где  — статический вертикальный прогиб конструкции от веса груза в месте его приложения (грузовая тележка, концевые блоки стрелы и т. п.), значения
— статический вертикальный прогиб конструкции от веса груза в месте его приложения (грузовая тележка, концевые блоки стрелы и т. п.), значения  см. в табл.;
см. в табл.;  — поправочный коэффициент. Для отдельных групп кранов значение
— поправочный коэффициент. Для отдельных групп кранов значение  устанавливается на основании дополнительных исследований, зависящих от способа запуска двигателя механизма подъема. При отсутствии таких данных для кранов общего назначения можно принимать
устанавливается на основании дополнительных исследований, зависящих от способа запуска двигателя механизма подъема. При отсутствии таких данных для кранов общего назначения можно принимать 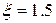 . Частота собственных колебаний конструкции G грузом как для системы с одной степенью свободы
. Частота собственных колебаний конструкции G грузом как для системы с одной степенью свободы 
Динамический коэффициент нагрузки в канате  при подъеме груза с жесткого основания с подхватом или при мгновенном торможении опускающегося груза может быть определен в соответствии с одномассовой расчетной схемой (рис. 3.6, б) в виде:
при подъеме груза с жесткого основания с подхватом или при мгновенном торможении опускающегося груза может быть определен в соответствии с одномассовой расчетной схемой (рис. 3.6, б) в виде:  ,
,
где 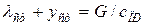 (
( — приведенная к грузовым канатам суммарная жесткость канатов и конструкции крана). При абсолютно жесткой конструкции
— приведенная к грузовым канатам суммарная жесткость канатов и конструкции крана). При абсолютно жесткой конструкции 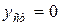 и
и 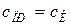 ; при этом механизм подъема и рама тележки будут испытывать наибольшую нагрузку.
; при этом механизм подъема и рама тележки будут испытывать наибольшую нагрузку.
Период продольных колебаний  груза массой
груза массой 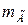 на канатах длиной Н:
на канатах длиной Н:
 ,
,
для средних условий (напряжение растяжения  = 240 МПа и модуль упругости каната
= 240 МПа и модуль упругости каната  МПа)
МПа)  .
.
Вследствие несимметричности схемы нагружения некоторых типов кранов при работе механизма подъема груза (например, стреловые и козловые краны) помимо вертикальных возникают горизонтальные нагрузки  , которые по величине могут иметь один порядок с вертикальными. Точное определение
, которые по величине могут иметь один порядок с вертикальными. Точное определение  связано с решением систем дифференциальных уравнений; приближенно значения
связано с решением систем дифференциальных уравнений; приближенно значения  могут быть найдены из рассмотрения соотношений между податливостью конструкции в вертикальном и горизонтальном направлениях. Для козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно динамическая составляющая горизонтальной нагрузки
могут быть найдены из рассмотрения соотношений между податливостью конструкции в вертикальном и горизонтальном направлениях. Для козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно динамическая составляющая горизонтальной нагрузки  может быть определена:
может быть определена:
 ,
,
где 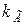 — коэффициент горизонтальной динамической нагрузки; G — вес груза на канатах;
— коэффициент горизонтальной динамической нагрузки; G — вес груза на канатах;  — динамический коэффициент нагрузки на металлоконструкцию.
— динамический коэффициент нагрузки на металлоконструкцию.
Значения динамических коэффициентов  для портальных кранов
для портальных кранов
| Тип портального крана | Случаи нагрузок | |
| I | II | |
| Монтажный Крюковой Грейферный | – 1.3 1.4 | 1.3 1.5 1.6 |

Рисунок 3.7 - Значения динамических коэффициентов  для мостовых и козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно в зависимости от скорости подъема груза: 1 — короткозамкнутый электродвигатель; 2 – фазный электродвигатель, реостатный пуск; 3 — система плавного регулирования скорости
для мостовых и козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно в зависимости от скорости подъема груза: 1 — короткозамкнутый электродвигатель; 2 – фазный электродвигатель, реостатный пуск; 3 — система плавного регулирования скорости
Значения коэффициента горизонтальной динамической нагрузки 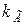 для козловых кранов общего назначения грузоподъемностью от 1 до 60 т включительно
для козловых кранов общего назначения грузоподъемностью от 1 до 60 т включительно
| Схема крана | Расположение грузовой тележки | 
|
| С гибкой и жесткой опорами | Консоль жесткой опоры Середина пролета Консоль гибкой опоры | 0,60 0,45 0,30 |
| С обеими жесткими опорами | Консоль опоры (любой) Середина пролета | 0,15 |
При передвижении крана (тележки) вертикальные динамические нагрузки, возникающие из-за неровности пути (толчки), учитываются коэффициентом толчков  ; для других типов кранов его можно принимать при скорости передвижения v (м/с):
; для других типов кранов его можно принимать при скорости передвижения v (м/с):
v <1,0 1,0—1,5 1,6—3,0 >3,0
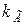 1,0 1,1(1,05) 1,2(1,1) 1,3(1,15)
1,0 1,1(1,05) 1,2(1,1) 1,3(1,15)
Коэффициенты толчков 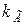 для мостовых кранов общего назначения грузоподъемностью от 1 до 50 т включительно
для мостовых кранов общего назначения грузоподъемностью от 1 до 50 т включительно
| Скорость передвижения крана м/с | 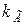
| |
| Стыки на болтовых накладках | Сварные механически обработанные стыки; отсутствие стыков | |
| До 0,5 0.5 до 1 Св. 1 | До 0,83 0,83 до 1,6 Св. 1,6 | 1,0 1,1 1,2 |
Примечания: 1. Для кранов с балансирными тележками  2. При укладке крановых рельсов на упругой подкладке
2. При укладке крановых рельсов на упругой подкладке 
|
При заваренных стыках рельсов, а также при их отсутствии, при подрессоренных ходовых частях рекомендуемые значения 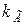 приведены в скобках.
приведены в скобках.
В нормах расчета коэффициент толчков при движении по крановому пути определяется по формуле:  где
где  — скорость движения, м/мин, а — коэффициент, равный 0,001 при заваренных стыках или при их отсутствии и 0,002 при открытых стыках рельсов.
— скорость движения, м/мин, а — коэффициент, равный 0,001 при заваренных стыках или при их отсутствии и 0,002 при открытых стыках рельсов.
При пневмоколесном ходе по аналогии с данными для грузовых машин (рессоры, скорость 20—50 км/ч) можно принимать 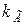 =1.5 для асфальтированных и
=1.5 для асфальтированных и 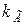 =2.0 для булыжных дорог.
=2.0 для булыжных дорог.
При расчете по второму случаю нагрузок на коэффициент толчков следует умножать как вес конструкции, так и вес груза, имея в виду минимальную длину его подвеса. При расчете по первому случаю нагрузок для конструкции и груза в среднем можно принимать
 .
.
При передвижении крана (тележки) максимальное ускорение  во время разгона или торможения ограничивается условием сцепления колес с рельсами:
во время разгона или торможения ограничивается условием сцепления колес с рельсами:
 ,
,
где  — давление на приводные колеса (с учетом влияния горизонтальных инерционных сил, ветра и поперечных раскачиваний груза);
— давление на приводные колеса (с учетом влияния горизонтальных инерционных сил, ветра и поперечных раскачиваний груза);  — масса тележки (крана) с грузом или без него;
— масса тележки (крана) с грузом или без него;  — коэффициент сцепления колес с рельсами (
— коэффициент сцепления колес с рельсами ( =0,2 для кранов, работающих в закрытых помещениях; для работающих на открытом воздухе
=0,2 для кранов, работающих в закрытых помещениях; для работающих на открытом воздухе  =0,12;
=0,12;  =0,25 — на открытом воздухе с применением песочниц).
=0,25 — на открытом воздухе с применением песочниц).
Горизонтальные инерционные поперечные нагрузки, приложенные в месте контакта ходовых колес с рельсами, принимаются для грузовых тележек равными 0,1 от сил давления на колесо. Для козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно должны учитываться динамические перекосные нагрузки, возникающие при внезапном замыкании одного из тормозов механизма передвижения крана.
При вращении поворотной части крана с частотой вращения  возникают центробежные силы инерции
возникают центробежные силы инерции  (где
(где  — масса элемента крана, расположенная на расстоянии
— масса элемента крана, расположенная на расстоянии  от оси вращения), а во время разгона и торможения поворотной части с угловым ускорением
от оси вращения), а во время разгона и торможения поворотной части с угловым ускорением  касательные силы инерции
касательные силы инерции  . При наличии муфты предельного момента с моментом МM приведенным к оси вращения крана, максимальное угловое ускорение
. При наличии муфты предельного момента с моментом МM приведенным к оси вращения крана, максимальное угловое ускорение  поворотной части:
поворотной части:
 ,
,
где  — приведенный к оси вращения крана момент инерции масс поворотной части крана; Мс — момент статических сил сопротивления вращению (трение, составляющая веса, ветер); знак плюс принимается, если момент сил инерции и Мс направлены в разные стороны, знак минус — если в одну.
— приведенный к оси вращения крана момент инерции масс поворотной части крана; Мс — момент статических сил сопротивления вращению (трение, составляющая веса, ветер); знак плюс принимается, если момент сил инерции и Мс направлены в разные стороны, знак минус — если в одну.
Раскачивания груза на канатах возникают при разгонах и торможениях механизмов передвижения, вращения и изменения вылета крана; давлении ветра на груз; при наезде на концевые упоры (буферы); качке крана на воде. В поворотных кранах главную роль играет механизм вращения.
При моделировании подвеса груза на канатах в виде математического маятника длиной Н при отклонении грузовых канатов от положения равновесия на угол α горизонтальная нагрузка на кран  . При постепенном нарастании движущей (тормозной) силы
. При постепенном нарастании движущей (тормозной) силы  ,где
,где  — линейное ускорение точки подвеса груза. При мгновенном приложении силы и достаточной длительности ее действия
— линейное ускорение точки подвеса груза. При мгновенном приложении силы и достаточной длительности ее действия  .
.

Рисунок 3.8 - Схема раскачивания груза на канатах
как математического маятника
Период поперечных колебаний груза с массой mГ при неподвижной абсолютно жесткой конструкции  , при движущейся конструкции с приведенной к точке подвеса груза массой mк
, при движущейся конструкции с приведенной к точке подвеса груза массой mк
 .
.
Величины углов отклонения  канатов от положения равновесия зависят от типа крана и режима его эксплуатации. Они могут задаваться в виде фиксированных значений, полученных на основе данных натурных исследований кранов. По нормам для мостовых и козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно
канатов от положения равновесия зависят от типа крана и режима его эксплуатации. Они могут задаваться в виде фиксированных значений, полученных на основе данных натурных исследований кранов. По нормам для мостовых и козловых кранов общего назначения грузоподъемностью от 1 до 50 т включительно  . Если данные натурных исследований отсутствуют, то в поворотных кранах можно принимать для второго случая нагрузок наибольший тангенс угла отклонения канатов
. Если данные натурных исследований отсутствуют, то в поворотных кранах можно принимать для второго случая нагрузок наибольший тангенс угла отклонения канатов
 ,
,
где  — средние касательное и центробежное ускорения точки подвеса груза при вращении на максимальном вылете соответственно;
— средние касательное и центробежное ускорения точки подвеса груза при вращении на максимальном вылете соответственно;  — то же при изменении вылета (или передвижении, если оно является рабочим движением);
— то же при изменении вылета (или передвижении, если оно является рабочим движением);  —сила ветра на груз для II случая нагружения.
—сила ветра на груз для II случая нагружения.
Для I случая нагружения средний угол отклонения можно принимать
 .
.
Углы отклонения канатов от вертикали для портальных кранов
| Тип портального крана | Случаи нагрузок | Углы для расчета мощности двигателей | ||||
| I | II | |||||

| 
| 
| 
| 
| 
| |
| Грейферный Крюковой Монтажный | 6.5 - | 5.5 4.5 - | 13.5 | 5.5 4.5 | ||
Примечание,  — в плоскости качания стрелы, — в плоскости качания стрелы, 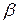 – перпендикулярно к плоскости качания стрелы. – перпендикулярно к плоскости качания стрелы.
|
Углы  при вращении крана могут располагаться как вдоль, так и поперек стрелы. При косом подъеме груза в расчетах принимается, что угол
при вращении крана могут располагаться как вдоль, так и поперек стрелы. При косом подъеме груза в расчетах принимается, что угол  может достигать
может достигать  и угол
и угол  .
.
В общем случае при пространственной запасовке грузовых канатов раскачивания груза не следуют закону математического маятника. Так, для схемы подвеса груза по рис 3.9 частота собственных колебаний при поперечных раскачиваниях
 ,
,
где коэффициент жесткости  и приведенная к координате x (рис.3.9) масса
и приведенная к координате x (рис.3.9) масса  груза
груза 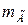 с учетом его момента инерции
с учетом его момента инерции 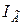 относительно центральной оси, перпендикулярной к плоскости рис. [
относительно центральной оси, перпендикулярной к плоскости рис. [  >
> 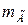 , так как груз при колебаниях совершает кроме поступательного и вращательное движение, поворачиваясь на угол
, так как груз при колебаниях совершает кроме поступательного и вращательное движение, поворачиваясь на угол  ]:
]:
 ;
;
 ,
,
где  ;
;  — вес груза,
— вес груза,  — квадрат радиуса инерции груза. Тригонометрические функции углов
— квадрат радиуса инерции груза. Тригонометрические функции углов  ,
, 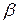 :
:
 ;
;
длины канатов 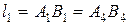 ,
,  ,
,
 .
.

Рисунок 3.9 - Схема раскачивания груза на пространственном подвесе:
Аi. — точки касания канатами барабана, блоков или шарниры крепления
канатов; Вi Bi/ - точки касания канатами блоков подвески в положении
равновесия и при отклоненном положения груза соответственно; М и М/ - центр масс груза в положении равновесия и в процессе колебаний соответственно;
Н – длина подвеса груза; l — расстояние от центра масс груза до плоскости, в которой лежат оси блоков; r — радиус блоков; f, d, b, s — характерные размеры подвеса груза;  ,
, 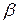 — углы наклона канатов к вертикали в положении
— углы наклона канатов к вертикали в положении
равновесия;  ,
,  — углы отклонения канатов от положений равновесия
— углы отклонения канатов от положений равновесия
Углы  ,
, 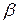 могут быть как положительными, так и отрицательными, что определяется знаком синусов в формулах. Если центр масс груза (точка М на рис. лежит выше плоскости, в которой расположены оси блоков, то в выражения h следует подставлять с противоположным знаком.
могут быть как положительными, так и отрицательными, что определяется знаком синусов в формулах. Если центр масс груза (точка М на рис. лежит выше плоскости, в которой расположены оси блоков, то в выражения h следует подставлять с противоположным знаком.






