Для заданной шарнирно опертой балки необходимо найти три опорные реакции:  ,
,  и
и  . Поскольку на балку действуют только вертикальные нагрузки, перпендикулярные к ее оси, горизонтальная реакция неподвижной шарнирной опоры A равна нулю:
. Поскольку на балку действуют только вертикальные нагрузки, перпендикулярные к ее оси, горизонтальная реакция неподвижной шарнирной опоры A равна нулю:  .
.
Направления вертикальных реакций  и
и  выбираем произвольно. Направим, например, обе вертикальные реакции вверх. Для вычисления их значений составим два уравнения статики:
выбираем произвольно. Направим, например, обе вертикальные реакции вверх. Для вычисления их значений составим два уравнения статики:
 ;
; 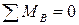 .
.
Напомним, что равнодействующая погонной нагрузки  , равномерно распределенной на участке длиной l, равна
, равномерно распределенной на участке длиной l, равна  , то есть равна площади эпюры этой нагрузки и приложена она в центре тяжести этой эпюры, то есть посредине длины.
, то есть равна площади эпюры этой нагрузки и приложена она в центре тяжести этой эпюры, то есть посредине длины.
Тогда

 кН;
кН;
 ;
;
 кН.
кН.
Делаем проверку:  .
.
Напомним, что силы, направление которых совпадает с положительным направлением оси y, проектируются (проецируются) на эту ось со знаком плюс:


 ,
,
то есть верно.
Строим эпюры перерезывающих сил 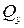 и изгибающих моментов
и изгибающих моментов 
Разбиваем длину балки на отдельные участки. Границами этих участков являются точки приложения сосредоточенных усилий (активных и/или реактивных), а также точки, соответствующие началу и окончанию действия распределенной нагрузки. Таких участков в нашей задаче получается три. По границам этих участков наметим шесть поперечных сечений, в которых мы и будем вычислять значения перерезывающих сил и изгибающих моментов (рис. 3.13, а).
Сечение 1. Отбросим мысленно правую часть балки. Для удобства вычисления перерезывающей силы  и изгибающего момента
и изгибающего момента  , возникающих в этом сечении, закроем отброшенную нами часть балки листком бумаги, совмещая левый край листка бумаги с самим сечением.
, возникающих в этом сечении, закроем отброшенную нами часть балки листком бумаги, совмещая левый край листка бумаги с самим сечением.
Перерезывающая сила в сечении балки равна алгебраической сумме всех внешних сил (активных и реактивных), которые мы видим. В данном случае мы видим реакцию опоры  и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
 кН.
кН.
Знак «плюс» взят потому, что сила  вращает видимую нами часть балки относительно первого сечения (края листка бумаги) по ходу часовой стрелки.
вращает видимую нами часть балки относительно первого сечения (края листка бумаги) по ходу часовой стрелки.
Изгибающий момент в сечении балки равен алгебраической сумме моментов всех усилий, которые мы видим, относительно рассматриваемого сечения (то есть относительно края листка бумаги). Мы видим реакцию опоры  и погонную нагрузку q, распределенную на бесконечно малой длине. Однако у силы
и погонную нагрузку q, распределенную на бесконечно малой длине. Однако у силы  плечо равно нулю. Равнодействующая погонной нагрузки также равна нулю. Поэтому
плечо равно нулю. Равнодействующая погонной нагрузки также равна нулю. Поэтому
 .
.
Сечение 2. По-прежнему будем закрывать листком бумаги всю правую часть балки. Теперь мы видим реакцию  и нагрузку q, действующую на участке длиной
и нагрузку q, действующую на участке длиной 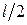 . Равнодействующая погонной нагрузки равна
. Равнодействующая погонной нагрузки равна  . Она приложена посредине участка длиной
. Она приложена посредине участка длиной 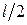 . Поэтому
. Поэтому
 кН;
кН;
 кН·м.
кН·м.
Напомним, что при определении знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении (то есть левый край листка бумаги нами мысленно представляется жесткой заделкой).
Сечение 3. Закроем правую часть. Получим
 кН;
кН;
 кН·м.
кН·м.
Сечение 4. Закрываем листком правую часть балки. Тогда
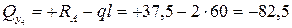 кН;
кН;
 кН·м.
кН·м.
Теперь, для контроля правильности вычислений, закроем листком бумаги левую часть балки. Мы видим сосредоточенную силу P, реакцию правой опоры  и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
и погонную нагрузку q, распределенную на бесконечно малой длине. Равнодействующая погонной нагрузки равна нулю. Поэтому
 кН;
кН;
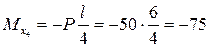 кН·м.
кН·м.
То есть все верно.
Сечение 5. По-прежнему закроем левую часть балки. Будем иметь
 кН;
кН;
 кН·м.
кН·м.
Сечение 6. Опять закроем левую часть балки. Получим
 кН;
кН;
 .
.
По найденным значениям строим эпюры перерезывающих сил  (рис. 3.13, б) и изгибающих моментов
(рис. 3.13, б) и изгибающих моментов  (рис. 3.13, в).
(рис. 3.13, в).
Убеждаемся в том, что под незагруженным участком эпюра перерезывающих сил идет параллельно оси балки, а под распределенной нагрузкой q – по прямой, имеющей наклон вниз. На эпюре  имеется три скачка: под реакцией
имеется три скачка: под реакцией  – вверх на 37,5 кН, под реакцией
– вверх на 37,5 кН, под реакцией  – вверх на 132,5 кН и под силой P – вниз на 50 кН.
– вверх на 132,5 кН и под силой P – вниз на 50 кН.
На эпюре изгибающих моментов мы видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой интенсивностью q эпюра изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. Под сосредоточенным моментом – скачок на 60 кН ·м, то есть на величину самого момента. В сечении 7 на эпюре  – экстремум, поскольку эпюра перерезывающей силы для этого сечения проходит через нулевое значение (
– экстремум, поскольку эпюра перерезывающей силы для этого сечения проходит через нулевое значение ( ). Определим расстояние
). Определим расстояние  от сечения 7 до левой опоры.
от сечения 7 до левой опоры.
Перерезывающая сила
 .
.
Отсюда
 м.
м.
Экстремальное значение изгибающего момента в сечении 7 равно:
 кН·м.
кН·м.






