Пусть дано уравнение плоскости  и произвольная точка
и произвольная точка  .
.

| Возможно, она лежит в плоскости (тогда расстояние по формуле автоматически получится 0). Но в общем случае она не принадлежит плоскости. Мы не знаем, где основание перпендикуляра, более того, его и не потребуется искать. |
Возьмём произвольную точку 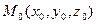 в плоскости. Сделать это просто: присвоим какие-нибудь значения 2 переменным из трёх, и вычислим третью. Например, как правило, задать x,y и вычислить z.
в плоскости. Сделать это просто: присвоим какие-нибудь значения 2 переменным из трёх, и вычислим третью. Например, как правило, задать x,y и вычислить z.
Итак, выбрали какую-то точку в плоскости. Отрезок между  и
и  не перпендикулярен плоскости, но его проекция на нормаль - это как раз и есть кратчайшее расстояние до плоскости (d).
не перпендикулярен плоскости, но его проекция на нормаль - это как раз и есть кратчайшее расстояние до плоскости (d).
 =
= 
 .
.
Если подставить в уравнение плоскости (в числителе) точку, лежащую в плоскости, то получим 0. Поэтому и получится d=0. В общем же случае, результат подстановки некоторой точки, не лежащей в плоскости, в уравнение плоскости, характеризует удаление от плоскости.
Пункт 4. Взаимное расположение плоскостей
Пусть даны 2 плоскости.
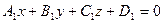
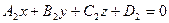
Если рассматривать это как систему уравнений, то видим, что 2 уравнения и 3 переменных, то есть по меньшей мере одна свободная переменная. Это означает, что если решения есть, то их бесконечно много. Это и есть все точки, принадлежащие прямой, являющейся пересечением плоскостей.
Чтобы найти пересечение, достаточно решить систему уравнений, где 2 уравнения - это и есть уравнения этих плоскостей.
Если 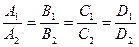 то плоскости совпадают, так как уравнения полностью пропорциональны.
то плоскости совпадают, так как уравнения полностью пропорциональны.
Если 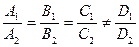 то плоскости параллельны. Дело в том, что если из одного уравнения вычесть кратное второму, то получим все 0 коэффициенты при x, y, z, и останется противоречивое уравнение (некая ненулевая константа = 0).
то плоскости параллельны. Дело в том, что если из одного уравнения вычесть кратное второму, то получим все 0 коэффициенты при x, y, z, и останется противоречивое уравнение (некая ненулевая константа = 0).
Если пропорциональность нарушена среди каких-то из первых 3 дробей, то плоскости пересекаются по прямой.
Пункт 5. Угол между плоскостями и метод его нахождения.
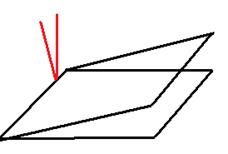
| Можно искать как угол между нормалями 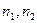 (показаны красным). Их координаты известны - это (показаны красным). Их координаты известны - это  и и 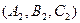 . В то же время известно, что . В то же время известно, что 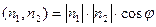 . Тогда . Тогда 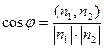 = = 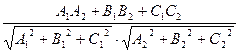 . .
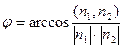 . .
|
Прямая в пространстве.
Для прямой на плоскости и для плоскости в пространстве есть однозначно определённое направление нормали (перпендикуляра) т.к. там размерности рассматриваемых многообразий 1 и 2 (2 и 3 соответственно), то есть «не хватает» одной размерности. А для прямой в пространстве не хватает 2 размерностей (1 и 3). Это совершенно новый случай, здесь нельзя однозначно задать перпендикуляр. Есть целая плоскость, перпендикулярная прямой, то есть бесконечное число нормалей. А вот направляющий вектор однозначно определён (с точность до его длины, конечно). Это проявится в том, что мы получим другой тип уравнений.
п.1. Построение уравнения прямой по точке и направляющему вектору.

| Пусть дана точка  с координатами с координатами 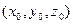 и направляющий вектор и направляющий вектор  (выделен жирно на чертеже)
Представим себе, что какая-то произвольная точка (выделен жирно на чертеже)
Представим себе, что какая-то произвольная точка 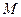 с координатами с координатами 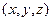 лежит на этой же прямой.
Тогда лежит на этой же прямой.
Тогда  и и 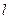 коллинеарны, то есть их координаты - пропорциональны, т.е. коллинеарны, то есть их координаты - пропорциональны, т.е. 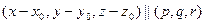
|
тогда  . Это канонические уравнения прямой в пространстве.
. Это канонические уравнения прямой в пространстве.
Фактически здесь не одно а два уравнения, впрочем, это понятно: ведь прямая может быть задана как пересечение 2 плоскостей. Кстати, если перемножить 1-ю и 2-ю пропорции независимо друг от друга, и свести к обычным уравнениям, то мы и получили бы уравнения каких-то 2 плоскостей.
Если эти 3 дроби равны, то можно приравнять их к некоторому параметру t.
 . Если теперь выразим x,y,z через t из каждой дроби по отдельности, получим:
. Если теперь выразим x,y,z через t из каждой дроби по отдельности, получим:
 - параметрические уравнения. Это физические уравнения движения, в момент времени t=0 находимся в точке
- параметрические уравнения. Это физические уравнения движения, в момент времени t=0 находимся в точке 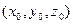 , в момент времени t=1 сдвинулись к концу направляющего вектора.
, в момент времени t=1 сдвинулись к концу направляющего вектора.
Векторный вид записи этих 3 равенств: 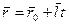 . При t=0 радиус-вектор из начала координат к исходной точке, через 1 секунду он будет направлен в конец вектора
. При t=0 радиус-вектор из начала координат к исходной точке, через 1 секунду он будет направлен в конец вектора 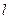 .
.
Пример. Точка (1,1,1) направляющий вектор (1,2,3).
 , тогда
, тогда 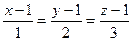 - канонические уравнения.
- канонические уравнения.
Параметрические: 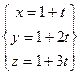
Если привести 2 пропорции 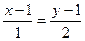 и
и 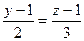 то получим
то получим
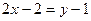 и
и 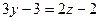 , то есть
, то есть  и
и 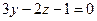
это и есть уравнения двух плоскостей, в пересечении который лежит эта прямая.
Замечание. Если требуется построить уравнение прямой по 2 точкам, то направляющий вектор от 1-й ко 2-й точке, и далее известный алгортим.






