1. Вычислить определитель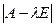 
и приравнять к нулю - получится характеристическое уравнение.
2. Решить характеристическое уравнение 
, найти все собственные числа.
Их будет не больше, чем n, так как уравнение порядка n, так как по диагонали n элементов.
3. Подставить каждое конкретное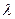 
в характеристическую матрицу, и решить однородную систему 
. Таких шагов может быть n. Каждый раз надо изменить диагональ и заново решить систему!
ФСР системы это и будет собственный вектор для того .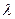
Пример. Найти собственные числа и векторы для 
.
= 
. Далее, 
. Тогда уравнение 
.
Рещим это уравнение: 
. Получим 
.
Теперь подставим каждое 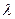и решим системы уравнений.
:
, 
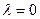, система: 
. Общее решение: 
, вектор 
.
:
, 
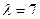, система: 
. Общее решение: 
, вектор 
.
Проверка:
, 
.
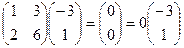Никакого третьего собственного числа в этом примере быть не может, так как матрица порядка 2, и характеристическое уравнение степени 2.
Теорема 5. Если базис состоит из собственных векторов, то матрица оператора в этом базисе диагональна.
Доказательство.
, то есть 1-й столбец в матрице оператора это такие числа: 
.
Аналогично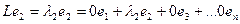 
, то есть 2-й столбец 
. И т.д.
Таким образом, получится матрица оператора: 
.
Теорема 6. Следующее свойство (Ax,y) = (x,Ay) выполняется 
матрица А симметрична (то есть 
).
Доказательство. Рассмотрим это равенство для базисных векторов: 
. Если оно выполняется для любой пары базисных векторов, то есть для любых индексов i, j.
, как показано раньше, это i-й столбец матрицы линейного оператора. Если скалярно умножить его на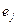 
, то есть на тот вектор, где все координаты 0 и только на месте j единица, - получим j - й элемент из i - го столбца, это 
в матрице.
Аналогично,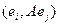 
это i - й элемент из j - го столбца, то есть 
.
Таким образом, эквивалентно тому, что = для всех индексов i, j.
Определение. Если для линейного оператора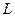 
, для любой пары векторов 
верно 
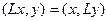, то 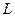называется симметрическим оператором.
Лекция № 6. 07. 10. 2016
Теорема 7. Собственные векторы симметрического оператора, соответствующие разным 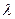, ортогональны.
Доказательство. Дано: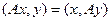 
, пусть первый вектор собственный и соответствует 
, а второй 
. То есть верно: 
и 
. Тогда 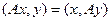можно записать в виде 
, тогда 
, тогда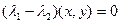 
. Собственные числа разные, поэтому первый множитель не равен 0, тогда 
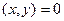. Скалярное произведение 0, векторы ортогональны.
Следствие. Для линейного оператора, матрица которого симметрична, существует ортогональный базис, состоящий из собственных векторов.
Квадратичные формы.
Билинейная форма, её задание с помощью матрицы.
Рассмотрим подробнее скалярное произведение типа 
, А - матрица некоторого линейного оператора. Произведение квадратной матрицы на столбец 
это вектор-столбец, затем его скалярно умножаем на вектор 
, в итоге получится число. Таким образом, это некоторая скалярная функция от 2 векторов. Она линейна по каждому аргументу: если на 1 или 2 месте сумма векторов, то результат тоже представляется в виде суммы. Обозначим 
и назовём эту функцию билинейной формой.
Подробнее при n=2:
= 
= 
.
При произвольном n: 
здесь n2 слагаемых.
Фактически, это обобщённое скалярное произведение. Обычное скалярное произведение можно задать таким же способом, но с единичной матрицей Е: 
= 
. Это частный случай билинейной формы.
Теперь рассмотрим такой случай. Пусть билинейная форма вычисляется от 2 одинаковых векторов, 
. Обозначим 
и назовём эту функцию, отобрающую один вектор в число, квадратичной формой.
Квадратичная форма задаётся через скалярное произведение так: 
.
= 
.
Например, матрица 
задаёт такую квадратичную форму:
= 
= 
.
Очевидно, 
, то есть эта группа из двух слагаемых 
и 
может быть объединена. Коэффициенты 
и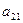 
распределить поровну. Так, 
это то же самое, что 
. Но ведь тогда матрицу квадратичной формы можно сделать симметричной, перераспределить эквивалентные элементы с сохранением их суммы. Таким образом, квадратичную форму всегда можно задать симметричной матрицей. Эта же самая квадратичная форма может быть задана и такой матрицей: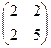 
.
Пример. Построить матрицу квадратичной формы
.
Решение. Распределим поровну коэффициенты:
. Каждый коэффициент, стоящий при 
, запишем на место 
.
Ответ: матрица: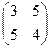 
.
* Очевидно, если матрица диагональна, то 
= 
квадратичная форма не содержит попарных произведений, а содержит только квадраты координат.
* Вспомним теорему 7 из прошлого §. Если матрица симметрична, то собственные векторы ортогональны.
* Вспомним также теорему 5 из прошлого §. Если в качестве нового базиса взять n собственных векторов, то матрица оператора в новом базисе будет диагональной.
Из всего сказанного следует, что квадратичную форму всегда можно привести к виду, не содержащему попарные произведения, а содержащему лишь квадраты, называется к «главным осям» (главные оси это направления, соответствующие собственным векторам).
Приведение к главным осям основано на поиске собственных чисел и векторов, примеры на эту тему решим подробно на практике.
