3.01. В опыте Юнга отверстия освещаются монохроматическим светом с длиной волны λ = 700 нм. Расстояние между отверстиями d = 1 мм, расстояние от отверстий до экрана L = 4 м. На каком расстоянии от центра экрана будет находиться первый максимум освещенности.
3.02. В опыте Юнга отверстия освещались монохроматическим светом (λ = 600нм). Расстояние между отверстиями d = 1 мм, расстояние от отверстий до экрана L = 3 м. Найти положение первых трех светлых полос.
3.03. В опыте с зеркалами Френеля расстояние между мнимыми изображениями d = 0,05 мм. Расстояние до экрана L = 5 м. В зеленом свете получились интерференционные полосы, расположенные на расстоянии
l = 5 мм друг от друга. Найти длину волны λ зеленого цвета.
3.04. Два параллельных световых пучка, отстоящих друг от друга на расстоянии d = 5 см, падают на кварцевую призму (n = 1, 49) с преломляющим углом a = 25°. Определите оптическую разность хода Δ этих пучков на выходе из призмы.
3.05. Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ = 0,6 мкм). Определите расстояние l от щелей до экрана, если ширина Δ х интерференционных полос равна 1,2 мм.
3.06. В опыте Юнга два когерентных источника S1 и S2 , излучающие свет с длиной волны λ = 0,6 мкм, находятся на расстоянии 2 мм друг от друга. Экран располагается на расстоянии 4 м от источников. Что будет наблюдаться в точке экрана расположенной на одной горизонтали с источником света S1: свет или темнота?
3.07. В опыте Юнга расстояние l от щелей до экрана равно 3 м. Определите угловое расстояние между соседними светлыми полосами, если третья световая полоса на экране отстоит от центра интерференционной картины на 4,5 мм.
3.08. Если в опыте Юнга на пути одного из интерферирующих лучей поставить перпендикулярно этому лучу тонкую стеклянную пластинку
(n = 1,5), то центральная светлая полоса смещается в положение, первоначально занимаемой пятой светлой полосой. Длина волны λ = 0,5 мкм. Определите толщину пластинки.
3.09. Установка для получения колец Ньютона освещается светом от ртутной дуги, падающим по нормали к поверхности пластинки. Наблюдение ведется в проходящем свете. Какое по порядку светлое кольцо, соответствующее линии λ 1 = 579,1 нм, совпадает со следующим кольцом, соответствующим линии λ 2 = 577 нм?
3.10. При освещении дифракционной решетки светом с длиной волны λ1 = 590 нм спектр третьего порядка виден под углом 10011/. Для какой длины волны λ2 спектр второго порядка, получаемый этой же решеткой, будет наблюдаться под углом 6016/?
3.11. Свет от монохроматического источника (λ = 600 нм) падает нормально на дифракционную решетку. Каков период этой решетки, если на экране расстояние между спектрами второго порядка l = 20 см? Решетка отстоит от экрана на расстояние L = 1м.
3.12. Точечный источник света (λ = 0,5 мкм) расположен на расстоянии a = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определите расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.
3.13. На узкую щель шириной a= 0,05 мм падает нормально монохроматический свет с длиной волны λ = 694 нм. Под каким углом будет наблюдаться вторая темная дифракционная полоса?
3.14. На щель шириной a = 6 λ падает нормально параллельный пучок монохроматического света с длиной волны λ. Под каким углом φ будет наблюдаться третий дифракционный минимум света?
3.15. На узкую щель падает нормально монохроматический свет. Его направление на четвертую темную дифракционную полосу составляет 2º 12΄. Определите, сколько длин волн укладывается на ширине щели.
3.16. Какое число штрихов N0 на единицу длины имеет дифракционная решетка, если зеленая линия ртути (λ = 546,1 нм) в спектре первого порядка наблюдается под углом φ = 19º 8΄?
3.17. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная d = 2 мкм.
3.18. Найти наибольший порядок k спектра для желтой линии натрия (λ = 589 нм), если постоянная дифракционной решетки d = 2 мкм.
3.19. Свет длиной волны λ = 589 нм нормально падает на дифракционную решетку с периодом d, общее количество штрихов которой составляет N = 10000 штрихов. Оценить угловую ширину максимума порядка m.
3.20. На дифракционную решетку, имеющую 100 штрихов на 1 мм, по нормали к ней падает белый свет. Найдите длину спектра первого порядка на экране, если расстояние от линзы до экрана 2 м. Видимым считать свет в диапазоне 400 - 760 нм.
3.21. В частично поляризованном свете амплитуда светового вектора, соответствующая максимальной интенсивности света, в n = 2 раза больше амплитуды, соответствующий минимальной интенсивности. Определить степень поляризации Р света.
3.22. Степень поляризации Р частично поляризованного света равна 0,5. Во сколько раз отличается максимальная интенсивность света, пропускаемого через анализатор, от минимальной.
3.23. Найти показатель преломления n стекла, если при отражении от него света отраженный луч будет полностью поляризован при угле β = 30°.
3.24. На николь падает пучок частично-поляризованного света. При некотором положении николя интенсивность света, прошедшего через него, стала минимальной. Когда плоскость пропускания николя повернули на угол β = 45°, интенсивность света возросла в k = 1,5 раза. Определить степень поляризации Р света.
3.25. Найти угол φ между главными плоскостями поляризатора и анализатора, если интенсивность естественного света проходящего через поляризатор и анализатор, уменьшается в 4 раза
3.26. Никотин (чистая жидкость), содержащийся в стеклянной трубке длиной l = 8 см, поворачивает плоскость поляризации желтого света натрия на угол φ = 137°. Плотность никотина ρ = 1,01∙103 кг/м3. Определить удельное вращение [ α ] никотина.
3.27. Степень поляризации частично поляризованного света составляет 0,75. Определите отношение максимальной интенсивности света, пропускаемого анализатором, к минимальной.
3.28. Угол поворота φ плоскости поляризации желтого света натрия при прохождении через трубку с раствором сахара равен 40°. Длина трубки l = 15 см. Удельное вращение [ α ] сахара равно 1,17∙10-2 рад∙м3/(м∙кг)
3.29. Угол между главными плоскостями поляризатора и анализатора составляет 30°. Определите изменение интенсивности прошедшего через них света, если угол между главными плоскостями равен 45°.
3.30. Определите степень поляризации Р света, который представляет собой смесь естественного света с плоскополяризованным, если интенсиность поляризованного света равна интенсивности естественного.
3.31. Найти температуру T печи, если известно, что излучение из отверстия в ней площадью S = 6,1 см2 имеет мощность N = 34,6 Вт. Излучение считать близким к излучению абсолютно черного тела.
3.32. Какую мощность N излучения имеет Солнце? Излучение Солнца считать близким к излучению абсолютно черного тела. Температура поверхности Солнца T = 5800 К.
3.33. Определите, как и во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с λ 1 = 720 нм до λ 2 = 400 нм.
3.34. Определить температуру Т, при которой излучательность R е абсолютно черного тела равна 10 кВт/м2.
3.35. Какую энергетическую светимость R 0 имеет абсолютно черное тело, если максимум спектральной плотности его энергетической светимости приходится на длину волны λ = 484 нм?
3.36. В каких областях спектра лежат длины волн, соответствующие максимуму спектральной плотности энергетической светимости, если источником света служит: а) спираль электрической лампочки (T = 3000 К); б) поверхность Солнца (T = 6000 К). Излучение считать близким к излучению абсолютно черного тела.
3.37. Муфельная печь потребляет мощность P = 1,4 кВт. Температура Т ее внутренней поверхности при открытом отверстии площадью S = 20 см2 равна 1,5 кК. Какая часть ε мощности рассеивается стенками, если считать, что отверстие печи излучает как абсолютно черное тело?
3.38. Определите, во сколько раз необходимо уменьшить термодинамическую температуру черного тела, чтобы его энергетическая светимость R e ослабилась в 16 раз.
3.39. Зачерненный шарик остывает от температуры T 1 = 300 К до T 2 = 293 К. На сколько изменилась длина волны λ, соответствующая спектральной плотности его энергетической светимости?
3.40. Принимая коэффициент черноты a T угля при температуре Т = 600 К равным 0,6, определить излучательность R е угля и энергию W, излучаемую с поверхности угля площадью S = 10 см2 за время t = 5 мин.
3.41. Найти частоту ν света, вырывающего из металла электроны, которые полностью задерживаются разностью потенциалов U = 3 Β. Красная граница фотоэффекта ν 0 = 6·1014 Гц. Найти работу выхода A электрона из металла.
3.42. При фотоэффекте с платиновой поверхности электроны полностью задерживаются разностью потенциалов U = 0,8 Β. Найти длину волны λ применяемого облучения и предельную длину волны λ0, при которой ещё возможен фотоэффект.
3.43. Максимальная скорость υ max фотоэлектронов, вылетающих из металла при облучении его γ - фотонами, равна 290 Мм/с. Определить энергию e γ - фотонов.
3.44. Задерживающее напряжение для платиновой пластинки (работа выхода A = 6,3 эВ) составляет 3,7 В. При тех же условиях для другой пластинки задерживающее напряжение равно 5,3 В. Определите работу выхода электронов из этой пластинки.
3.45. Красная граница фотоэффекта для бария λ = 5,5•10-7 м. С какой скоростью будут вылетать фотоэлектроны из бариевой пластинки при ее облучении светом с длиной волны λ = 4,4•10-7 м? Постоянная Планка h = 6,63•10-34 Дж•с, масса электрона m е = 9,1•10-31 кг.
3.46. Определите максимальную скорость ν max фотоэлектронов, вырываемых с поверхности цинка (работа выхода А = 4 эВ), при облучении γ - излучением с длиной волны λ = 2,47 пм.
3.47. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта λ о = 307 нм и максимальная кинетическая энергия Т max фотоэлектрона равна 1 эВ.
3.48. Найти задерживающую разность потенциалов U для электронов, вырываемых при освещении калия светом с длиной волны λ = 330 нм.
3.49. Длина волны света, соответствующей красной границе фотоэффекта, для некоторого металла λ 0 = 275 нм. Найти минимальную энергию фотона, вызывающего фотоэффект.
3.50. На цинковую пластинку падает монохроматический свет с длиной волны λ = 220 нм. Определить максимальную скорость υ max фотоэлектронов.
3.51. Фотон с энергией ε = 1,025 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона оказалась равной комптоновской длине волны λ с =2,43 пм.
3.52. Определить максимальное изменение длины волны при комптоновском рассеянии на свободных электронах.
3.53. Рентгеновские лучи с длиной волны λ 0 = 70,8 пм испытывают комптоновское рассеяние на парафине. Найти длину волны λ рентгеновских лучей, рассеянных в направлениях: а) φ = π / 2; б) φ = π
3.54. Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Оказывается, что длины волн рассеянного под углами θ 1 = 60о и θ 2 = 120о излучения отличаются в 1,5 раза. Определить длину волны падающего излучения, предполагая, что рассеяние происходит на свободных электронах.
3.55. Фотон длиной волны λ = 5 пм испытал комптоновское рассеяние под углом θ = 90о на первоначально покоившемся свободном электроне. Определить: 1) изменение длины волны при рассеянии; 2) энергию электрона отдачи; 3) импульс электрона отдачи.
3.56. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол θ = 180°? Энергия фотона ε до рассеяния равна 0,255 МэВ.
3.57. Какова была длина волны λ 0 рентгеновского излучения, если при комптоновском излучении этого излучения графитом под углом φ = 60о длина волны рассеянного излучения оказалась равной λ = 2,4 пм?
3.58. Фотон с энергией 0,3 МэВ рассеялся под углом θ = 180о на свободном электроне. Определить долю энергии фотона, приходящуюся на рассеянный фотон.
3.59. Фотон (λ = 1 пм) рассеялся на свободном электроне под углом θ = 90°. Какую долю своей энергии фотон передал электрону?
3.60. Рентгеновские лучи с длиной волны λ 0 = 20 пм испытывают комптоновское рассеяние под углом φ = 90о. Найти ∆ λ длины волны рентгеновских лучей при рассеянии, а также энергию W е и импульс p e электрона отдачи.
3.61. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).
3.62. На сколько изменилась кинетическая энергия в атоме водорода при излучении атомом фотона с длиной волны λ = 486 нм?
3.63. Используя теорию Бора для атома водорода, определить: 1) радиус ближайшей к ядру орбиты (первый Боровский радиус); 2) скорость движения электрона по этой орбите.
3.64. Определите 1) частоту n вращения электрона, находящегося на первой Боровский орбите; 2) эквивалентный ток.
3.65. Определите частоту света, излучаемого атомом водорода при переходе электрона на уровень с главным квантовым числом n = 2, если радиус орбиты электрона изменился в k = 9 раз.
3.65. Определите потенциальную и кинетическую энергии электрона, находящегося на первой орбите атома водорода.
3.66. Найти потенциал ионизации U 1 атома водорода.
3.67. Вычислить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.
3.68. Используя теорию Бора, определить орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода.
3.69. Определить длину волны, соответствующую третьей спектральной линии в серии Бальмера.
3.70. В каких пределах должны лежать длины волны λ монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус орбиты r k электрона увеличивается в 9 раз?
3.71. Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Определите вероятность обнаружения W электрона в средней трети ямы, если электрон находится в возбужденном состоянии (n = 3). Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.
3.72.. Электрон находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Определите вероятность обнаружения W электрона в крайней трети ямы, если электрон находится в возбужденном состоянии (n = 2).
3.73. Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Определите, во сколько раз изменится отношение разности соседних энергетических уровней Δ E n+1,n/Δ E n частицы при переходе от n = 3 к n' = 8.
3.74. Частица с энергией E движется в положительном направлении оси х и встречает на своем пути прямоугольный потенциальный барьер высотой U и конечной шириной l, причем E < U. Запишите уравнение Шредингера для областей 1, 2, 3.
3.75. Электрон с энергией E = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определите коэффициент D прозрачности потенциального барьера.
3.76. Частица с энергией E = 10 эВ движется в положительном направлении оси х, встречая на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 5 эВ. Определите коэффициент преломления n волн де Бройля на границе потенциального барьера.
3.77. Частица с энергией E = 50 эВ, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий потенциальный барьер высотой U = 20 эВ. Определите вероятность отражения частицы от барьера.
3.78. Частица массой m = 10-19 кг, двигаясь в положительном направлении оси х со скоростью υ = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите коэффициент отражения R волн де Бройля на границе барьера.
3.79. Частица с энергией E движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E < U. Запишите уравнение Шредингера для областей 1 и 2.
3.80. Протон с энергией Е = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определите вероятность W p прохождения протоном этого барьера. Во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона в вышеприведенных условиях?
ПРИЛОЖЕНИЯ
I. О ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЯХ
Числовые значения величин, с которыми приходится иметь дело при решении физических задач, являются большей частью приближенными.
К таким величинам относятся, в частности, многие константы, приводимые в справочниках. Например, для ускорения свободного падения в справочниках дается значение 9,81м/с, для отношения длины окружности к диаметру – 3,14, для массы электрона – 9,1·10-31кг и т.п. При более точном вычислении или измерении эти величины оказываются равными g = 9,80665 м/с2, p = 3,1416, m е = 9,106·10‾31кг. Однако и эти значения, в свою очередь, являются приближенными или в силу недостаточной точности измерения, или в силу того, что получены путем округления еще более точных значений.
Очень часто неопытные лица при вычислениях добиваются получения такой точности результатов, которая совершенно не оправдывается точностью использованных данных. Это приводит к бесполезной затрате труда t времени,
Рассмотрим такой пример. Пусть требуется определить плотность r вещества некоторого тела. При взвешивании тела на весах с точностью до 0,01г определили массу тела: m = (9,38 ± 0,01) г. Затем с точностью до 0,01 см3 был измерен объем тела: V = (3,463 ± 0,01) см3.
Без критического подхода к вычислениям можно получить такой результат: 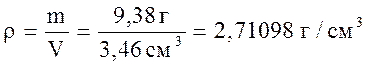
Но так как числа 9,38 и 3,46 приближенные, то последние цифры в этих телах сомнительны. Эти числа при измерении могли быть получены такими: первое – 9,39 или 9,37, второе – 3,45 или 3,47. В самом деле, при взвешивании с указанной выше точностью могла быть допущена погрешность на 0,01 как в сторону увеличения массы, так и в сторону ее уменьшения. То же: самое в отношении объема. Таким образом, плотность тела, если ее вычислять с точностью до пятого десятичного знака, как это сделано выше, могла оказаться
 ,
,
или
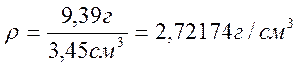 .
.
Сравнение всех трех результатов показывает, что они отличаются уже вторыми десятичными знаками и что достоверным является лишь первый десятичный знак, а второй – сомнительным. Цифры, выражающие остальные десятичные знаки, являются совершенно случайными не способны лишь ввести в заблуждение пользующегося вычисленными результатами. Следовательно, работа по вычислению большинства знаков затрачена впустую.
Во избежание бесполезных затрат труда и времени принято вычислять кроме достоверных знаков еще только один сомнительный.
В рассмотренном примере надо было вести вычисление до второго десятичного знака:
 .
.
Приближенные вычисления следует вести с соблюдением следующих правил.
1. При сложении и вычитании приближенных чисел окончательный результат округляют так, чтобы он не имел значащих цифр1 в тех разрядах, которые отсутствуют хотя бы в одном из приближенных данных. Например, при сложении чисел
4,462
+ 2,38
1,17273
1,0262
9,04093
следует сумму округлить до сотых долей, т.е. принять ее равной 9,04.
2. При умножении следует округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких цифр.
Например, вместо вычисления выражения
3,723·2,4·5,1846
следует вычислять выражение
3,7·2,4·5,2.
В окончательном результате необходимо оставлять такое же число значащих цифр, какое имеется в сомножителях, после их округления.
В промежуточных результатах следует сохранять на одну значащую цифру больше. Такое же правило соблюдается и при делении приближенным чисел.
3. При возведении в квадрат или в куб следует в степени брать столько значащих цифр, сколько их имеется в основании степени. Например,
1,322 » 1,74.
При извлечении квадратного или кубического корня в результате нужно брать столько значащих цифр, сколько их имеется в подкоренном выражении. Например, 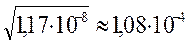
4. При вычислении сложных выражений следует применять указанные правила в соответствии с видом производимых действий. Например,
 .
.
Сомножитель 5,1 имеет наименьшее число значащих цифр – две. Поэтому результаты всех промежуточных вычислений должны округляться до трех значащих цифр:
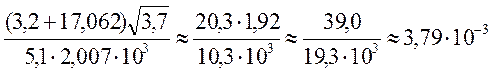 .
.
После округления результата до двух значащих цифр получаем 3,8*10-3. При вычислениях рекомендуем пользоваться калькулятором.
II.ТАБЛИЦЫ
Таблица 1. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН СИ,






