Задачи к контрольной работе № 1

 

1.01. Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением s = A + Bt ², где A = 8 м, В = - 2 м/с². Определить момент времени t, когда нормальное ускорение а _n точки равно 12 м/с². Найти скорость υ, тангенциальное а _τ и полное а ускорения точки в тот же момент времени t.

1.02. Две материальные точки движутся согласно уравнениям x ₁ = A ₁ t + + В ₁ t ² + С ₁ t ³ и x ₂ = A ₂ t + В ₂ t ² + С ₂ t ³, где A ₁ = 4 м/с, В ₁ = 8 м/с², C ₁ = - 16м/с³, A ₂ = 2 м/с, В ₂ = - 4 м/с², С ₂= 1 м/с³. В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости υ ₁ и υ ₂ точек в этот момент.

1.03. Материальная точка движется в плоскости ху согласно уравнениям x = A ₁ + В ₁ t + С ₁ t ² и y = A ₂ + В ₂ t +С ₂ t ², где В ₁ = 7 м/с, C ₁ = - 2 м/с², В ₂ = - 1 м/с, С ₂= 0,2 м/с². Найти модули скорости и ускорения точки в момент времени t = 5 c.

1.04. Зависимость пройденного телом пути s от времени t дается уравнением

s = A + Bt + Ct ² + Dt ³, где C = 0,14 м/с² и D = 0,01 м/с³. Через какое время t после начала движения тело будет иметь ускорение а = 1 м/с²? Найти среднее ускорение тела за этот промежуток времени.

1.05. Шар массой m = 10 кг и радиусом R = 0,2 м вращается вокруг оси, проходящей через его центр. Закон движения шара имеет вид φ = А + B t ² + C t ³, где В = 4 рад/с², С = - 1 рад/с³. Найти зависимость момента сил, действующих на шар, от времени. Чему будет равен момент сил М в момент времени t = 2 с?

1.06. Маховик, момент инерции которого J = 50 кг•м², вращается по закону: φ = А + B t + C t ², где А = 2 рад, В = 16 рад/с, С = - 2 рад/с². Найти закон изменения вращающего момента М и закон изменения мощности N. Чему равна мощность N ₁ в момент времени t = 3 с?

1.07. Зависимость пройденного телом пути s от времени t дается уравнением s = A t – B t ² + C t ³, где А = 2 м/с, В = 3 м/с² и С = 4 м/с³. Найти: 1) зависимость скорости υ и ускорения а от времени t; 2) путь s, пройденный телом, скорость υ и ускорение а тела через время t = 2 с после начала движения.

1.08. Зависимость пройденного телом пути s от времени t дается уравнением s = A + B t + C t ², где А = 3 м, В = 2 м/с и C = 1 м/с². Найти среднюю скорость и среднее ускорение тела за первую, вторую и третью секунды его движения.

1.09. Точка движется по прямой согласно закону х = A t + В t ³, где А = 6 м/с; В = - 0,125 м/с³. Определить: 1) среднюю скорость точки в интервале времени от t ₁ = 2 с до t ₂ = 6 с; 2) координату точки в тот момент времени, когда скорость тела будет равна нулю.

1.10. Материальная точка совершает колебания по закону . Определить 1) период колебаний, 2) максимальную скорость, 3) максимальное ускорение точки.

1.11. Тело брошено вертикально вверх с начальной скоростью υ _о = 4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью υ _о вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

1.12. Камень падает вертикально вниз с высоты 20 м. Начальная скорость равна нулю. Определите время падения камня, среднюю скорость падения камня.

1.13. Шарик бросают вертикально вверх со скоростью υ _о = 2 м/с с высоты h = 5 м. Определите 1) максимальную высоту подъема шарика; 2) время его падения на землю; 3) скорость в момент падения.

1.14. Два мяча бросают вертикально вверх из одной точки с одинаковыми скоростями 10 м/с с интервалом в 1 с. Определите, через какой промежуток времени после бросания первого мяча они встретятся в воздухе.

1.15. Пушка и цель находятся на одном уровне на расстоянии 5,1 км друг от друга. За какое время снаряд, выпущенный под произвольным углом к горизонту с начальной скоростью 240 м/с, достигнет цели? Сопротивлением воздуха пренебречь.

1.16. Камень, брошенный горизонтально, упал на землю через время t = 0,5 с на расстоянии l = 5 м по горизонтали от места бросания. С какой высоты h брошен камень? С какой скоростью υ _xон брошен?

1.17. Тело брошено под углом α = 30° к горизонту со скоростью υ _о = 30 м/с. Какова будет его скорость через время t = 1 с после начала движения?

1.18. Тело массой m = 0,5 кг брошено со скоростью υ _о = 10 м/с под углом α = 30° к горизонту. Пренебрегая сопротивлением воздуха, определите кинетическую T, потенциальную П и полную энергии тела: 1) через t = 0,4 c после начала движения; 2) в высшей точке траектории.

1.19. Какой начальной скоростью υ _о должна обладать сигнальная ракета, выпущенная под углом α = 45° к горизонту, чтобы она вспыхнула в наивысшей точке своей траектории? Время горения запала ракеты t = 6 c.

1.20. Вертолет летит горизонтально со скоростью υ = 160 км/ч на высоте h = 500 м. С вертолета нужно сбросить вымпел на остров. На каком по горизонтали расстоянии от острова летчик должен сбросить вымпел?

1.21. При горизонтальном полете со скоростью υ = 250 м/с, снаряд массой m = 8 кг разорвался на две части. Большая часть массой m ₁ = 6 кг получила ско­рость u ₁ = 400 м/с в направлении полета снаряда. Опре­делить модуль и направление скорости u ₂ меньшей части снаряда.

1.22. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом α = 30° к линии горизонта. Определить скорость u ₂ отката платформы, если снаряд вылетает со скоростью υ ₁ = 480 м/с. Масса платформы с орудием и снарядами m ₂= 18 т, масса снаряда m ₁ = 60 кг.

1.23. Конькобежец, стоя на коньках на льду, бросает камень массой m ₁ = 2,5 кг под углом α = 30° к горизонту со скоростью υ = 10 м/с. Какова будет начальная скорость υ _о движения конькобежца, если масса его m ₂ = 60 кг? Перемещением конькобежца во время броска пренебречь.

1.24. Человек массой m ₁ = 70 кг, бегущий со скоростью υ ₁ = 9 км/ч, догоняет тележку массой m ₂ = 190 кг, движущуюся со скоростью υ ₂ = 3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?

1.25. Снаряд, летевший со скоростью υ = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40 % от массы снаряда, полетел в противоположном направлении со скоростью и ₁ = 150 м/с. Определить скорость u ₂ большего осколка.

1.26. В деревянный шар массой m ₁ = 8 кг, подвешенный на нити длиной l = 1,8 м, попадает горизонтально летящая пуля массой m ₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3°? Размером шара пренебречь. Удар пули считать прямым, центральным.

1.27. Шар массой т ₁ = 1кг движется со скоростью υ ₁= 4 м/с и сталкивается с шаром массой m ₂ = 2 кг, движущимся навстречу ему со скоростью υ ₂ = 3 м/с. Каковы скорости и ₁и u ₂ шаров после удара? Удар считать абсолютно упругим, прямым, центральным.

1.28. Шар массой m ₁ = 5 кг движется со скоростью υ ₁ = 1 м/с и сталкивается с покоящимся шаром массой m ₂ = 2 кг. Определить скорости и ₁и u ₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

1.29. Шар массой m ₁ = 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40 % кинетической энергии. Определить массу m ₂ большего шара. Удар считать абсолютно упругим, прямым, центральным.

1.30. Из ружья массой m ₁ = 5 кг вылетает пуля массой m ₂ = 5 г со скоростью υ ₂ = 600 м/с. Найти скорость υ ₁ отдачи ружья.

1.31. Брусок массой m = 2 кг зажат между двумя вертикальными плоскостями с силой F = 10 Н. Найти ускорение бруска и силу трения между бруском и плоскостью при его проскальзывании. Какую минимальную вертикальную силу F _min нужно приложить к бруску, чтобы поднимать его вверх? Определить работу этой силы на пути 20 см. Коэффициент трения μ = 0,5.

1.32. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами m ₁ =150 г и m ₂ = 100 г, которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите: 1) ускорение грузов; 2) силу натяжения нити T, 3) работу силы тяжести, действующей на первый груз при опускании его на 40 см.

1.33. Через легкий неподвижный блок перекинута невесомая нить с двумя грузами на концах, массы которых m ₁ = 200 г и m ₂ = 140 г. Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов и силу натяжения нити. Трение в оси блока отсутствует. Определить работу силы тяжести, действующей на второй груз при его подъеме на 25 см.

1.34. Если к телу, находящемуся на горизонтальной поверхности, приложить силу F = 120 Н под углом α = 60° к горизонту, то тело будет двигаться равномерно. Найти среднюю мощность силы трения, если 60 см тело проходит за 10 с.

1.35. Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами М. Одновременно на каждый из грузов кладут по перегрузку: справа -массой З m, слева – m. Определить ускорение системы и силу натяжения нити, если М = 200 г, m = 50 г. Определить работу силы натяжения нити на пути 35 см.

1.36. Тело массой m = 5 кг скользит по наклонной плоскости, составляющей с горизонтом угол α = 45°. Зависимость пройденного телом пути от времени t дается уравнением s = C t ², где С = 1,73 м/с². Найти коэффициент трения тела о плоскость. Определить мощность в момент времени t = 2 мин.

1.37. На гладком столе лежит брусок массой m₁ = 4 кг. К бруску привязан шнур, перекинутый через неподвижный блок. К концу шнура подвешена гиря массой m₂ = 1 кг. Найти ускорение а, с которым движется брусок, и силу Т натяжения шнура. Массой блоков и трением пренебречь. Найти работу силы натяжения при передвижении гири на 0,5 м.

1.38. На столе стоит тележка массой m ₁ = 5 кг. К тележке привязан один конец шнура, перекинутого через блок. С каким ускорением a будет двигаться тележка, если к другому концу шнура привязать гирю массой m ₂ = 2 кг? Определить работу силы тяжести, действующей на гирю на пути 10 см.

1.39. Через блок перекинут шнур, к концам которого привязали грузы массами m ₁ = 1,5 кг и m ₂ = 3 кг. Какова будет сила натяжения нити во время движения грузов? Массой блока и шнура пренебречь. Определить работу силы тяжести, действующей на второй груз на пути 45 см.

1.40. Два бруска массами m ₁ = 1 кг и m ₂ = 4 кг, соединенные шнуром, лежат на столе. С каким ускорением а будут двигаться бруски, если к первому бруску приложить силу F = 10 Н, направленную горизонтально? Определить среднюю мощность этой силы за 3 с. Трением пренебречь.

1.41. Нить с привязанными к ее концам грузами массами т ₁ = 50 г и m ₂ = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение β = 1,5 рад/с². Трением и проскальзыванием нити по блоку пренебречь.

1.42. Диск массой m = 2 кг катится без проскальзывания по горизон­тальной плоскости со скоростью υ = 4 м/с. Найти кинетическую энер­гию Е _кдиска.

1.43. Маховик, момент инерции которого J = 63,6 кг•м², вращается с постоянной угловой скоростью ω = 31,4 рад/с. Найти тормозящий момент, под действием которого маховик останавливается через t = 20 с.

1.44. Маховик радиусом R = 0,2 м и массой m = 10 кг соединен с мотором при помощи ремня. Сила натяжения ремня, идущего без скольжения, постоянна и равна Т = 14,7 Н. Какое число оборотов в секунду будет делать маховик через промежуток времени ∆t = 10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.

1.45. К ободу колеса, имеющего форму диска, радиус которого R = 0,5 м и масса m = 50 кг, приложена касательная сила F = 100 Н. Найти: 1) угловое ускорение колеса β; 2) через какое время после начала действия силы колесо будет иметь частоту вращения n = 100 об/с.

1.46. Маховое колесо, имеющее момент инерции J = 24,5 кг•м², вращается, делая n = 20 об/с. Через промежуток времени ∆t = 1 мин после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.

1.47. Через неподвижный блок в виде сплошного диска перекинута нить, к концам которой привязаны грузы m ₁ = 100 г и m ₂ = 110 г. С каким ускорением будут двигаться грузы, если масса блока m = 400 г? Трением в блоке пренебречь.

1.48. Кинетическая энергия вращающегося маховика Е _к= 1 кДж. Под действием тормозящего момента маховик начал вращаться равнозамедлено и, сделав N = 80 оборотов, остановился. Определить момент М силы торможения.

1.49. Маховик, момент инерции которого J = 40 кг•м², из состояния покоя начал вращаться равноускоренно под действием момента силы М = 20 Н•м за t = 10 с. Определить кинетическую энергию Е _к, приобретенную маховиком.

1.50. Маховое колесо начинает вращаться с постоянным угловым ускорением β = 0,5 рад/с² и через t ₁ = 15 с после начала движения приобретает момент импульса L = 73,5 кг•м²/с. Найти кинетическую энергию колеса Е _кчерез t ₂= 20 с после начала движения.

1.51. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой т = 5кг каждая. Расстояние от каждой гири до оси скамьи l ₁= 70 см. Скамья вращается с частотой n ₁ = 1 с^-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l ₂ = 20 см? Момент инерции человека и скамьи (вместе) относительно оси J = 2,5 кг∙м².

1.51. Три баллона вместимости которых соответственно равны V ₁ = 3 дм³, V ₂ = 7 дм³, V ₃ = 5 дм³, наполнены один кислородом (р ₁ = 2·10⁵ Па), другой -азотом (р ₂ = 3·10⁵ Па) и третий - углекислым газом (р ₃ = 6·10⁴ Па) при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?

1.52. Два студента определяли плотность воздуха. Сначала они взвесили пустой сосуд и нашли, что его масса равна 20 г. Затем они надули мягкий сферический баллон из пластика до диаметра 21 см и выдавили его содержимое в сосуд. Масса сосуда с воздухом из баллона оказалась равной 26,5 г. Чему были равны плотность воздуха и его давление внутри баллона? Температура воздуха 20° С.

1.53. Определите плотность смеси водорода массой 4 г и кислорода массой 32 г при температуре 7° С и давлении 700 мм. рт. ст.

1.54. Плотность углекислотной (СО₂) атмосферы Венеры примерно в 50 раз выше плотности земной атмосферы при нормальных услови­ях. Считая, что температура у поверхности Венеры 477° С, найдите венерианское атмосферное давление.

1.55. Когда в течение длительного времени автомобиль идет по шос­се, особенно летом, камеры и заполняющий их воздух нагреваются в результате деформаций и трения, а также от соприкосновения с нагре­той поверхностью шоссе. На сколько процентов изменится давление в камере, если температура воздуха в камере повысится с 27° С до 30° С?

1.56. В сосуде вместимостью 1 л находится кислород массой 1 г. Определить концентрацию молекул кислорода в сосуде.

1.57. Сосуд содержит воздух при атмосферном давлении и температуре 20° С. До какой температуры нужно нагреть этот сосуд, чтобы из него вытиснилась одна пятая часть всех молекул, первоначально находившихся в сосуде?

1.58. В баллоне вместимостью 0,5 дм³ содержится смесь газов, со­стоящая из 10²⁰ молекул кислорода, 4·10²⁰ молекул азота и 3,3·10²⁰ мо­лекул аргона. Определите: 1) давление смеси; 2) молярную массу смеси. Температура смеси 127° С.

1.59. Баллон вместимостью 20 л наполнен сжатым воздухом. При температуре t ₁ = 20° С манометр показывает давление р ₁ = 1,2·10⁷ Па. Какой объем воды можно вытеснить из цистерны подводной лодки воздухом этого баллона, если вытеснение производится на глубине h = 30 м и температура на этой глубине равна t ₂ = 15° С? Атмосферное давление р _о = 10⁵ Па.

1.60. В цилиндр длиной l = 1,6 м, заполненный воздухом при нормальном атмосферном давлении p _о = 10⁵ Па, начали медленно вдвигать поршень площадью S = 200 см². Определить силу F, которая будет действовать на поршень, если его остановить на расстоянии l ₁ = 10 см от дна цилиндра.

1.61. При изотермическом расширении азота при температуре T = 280 К объем его увеличился в два раза. Определить: 1) совершенную при расширении газа работу А; 2) изменение внутренней энергии ΔU; 3) количество теплоты Q, полученное газом. Масса азота m = 0,2 кг.

1.62. Азот массой m = 0,1 кг был изобарно нагрет от температуры T ₁ = 200 К до температуры Т ₂ = 400 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение внутренней энергии азота ΔU.

1.63. Во сколько раз увеличится объем водорода, содержащий количество вещества v = 0,4 моль при изотермическом расширении, если при этом газ получит количество теплоты Q = 800 Дж? Температура водорода Т = 300 К.

1.64. Какая работа совершается при изотермическом расширении водорода массой m = 5 г, взятого при температуре Т = 290 К, если объем газа увеличивается в три раза? Определить полученное газом количество теплоты Q.

1.65. Определить работу, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты Q = 21 кДж. Найти также изменение внутренней энергии ΔU газа.

1.66. Азот массой m = 5 кг, нагретый на Δ T = 150 К, сохранил неизменный объем V. Найти: 1) количество теплоты Q, сообщенное газу; 2) изменение Δ U внутренней энергии; 3) совершенную газом работу A.

1.67. Водород занимает объем V ₁ = 10 м³ при давлении p ₁ = 100 кПа. Газ нагрели при постоянном объеме до давления p ₂ = 300 кПа. Определить: 1) изменение Δ U внутренней энергии газа; 2) работу А, совершаемую газом; 3) количество теплоты, сообщенное газу.

1.68. При изохорическом нагревании кислорода объемом V = 50 л давление газа изменилось на Δ p = 0,5 МПа. Найти количество теплоты, сообщенное газу.

1.69. Идеальный газ, совершающий цикл Карно, 70% количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определить: 1) термический КПД цикла; 2) работу, совершаемую при полном цикле.

1.70. Водород нагревался при постоянном давлении, причем ему было сообщено количество теплоты Q = 42 кДж. Определить работу А, которую совершил при этом газ, и изменение Δ U его внутренней энергии.

1.71. Двухатомный газ, находящийся при давлении 2 МПа и температуре 27 ⁰С, сжимается адиабатически, причем объем уменьшается вдвое. Найдите температуру и давление газа после сжатия.

1.72. При адиабатическом сжатии воздуха в цилиндре двигателя внутреннего сгорания давление изменяется от 0,1 МПа до 3,5 МПа. Начальная температура воздуха 25 ⁰С. Найдите температуру воздуха после сжатия.

1.73. Газ расширяется адиабатически, причем объем увеличивается вдвое, а температура падает в 1,32 раза. Какое число степеней свободы имеют молекулы этого газа?

1.74. Кислород объемом 8 л адиабатически сжимается до объема 2 л, при этом в конце сжатия устанавливается давление2 МПа. Под каким давлением находился газ до сжатия и какова была его температура?

1.75. До какой температуры охладится воздух, находящийся при температуре 0⁰С, если объем газа в результате адиабатического расширения увеличился втрое?

1.76. Двухатомный газ занимает объем 0,5 л при давлении 50 кПа. Газ адиабатически сжали, в результате чего объем его стал 100 мл. Найдите давление газа после сжатия и его температуру, если масса кислорода равна 0,4 г.

1.77. 10 г кислорода нагревается от 50 до 200 ⁰С. Найдите изменение энтропии, если нагревание происходит изохорически.

1.78. Найдите изменение энтропии и затраченную работу при изотермическом расширении 6 г водорода от 100 до 50 кПа.

1.79. 28 кг азота, находящегося при нормальных условиях, расширяется адиабатически в 5 раз. Найдите изменение внутренней энергии газа и совершенную работу.

1.80. 28 г азота, находящегося при температуре 25 ⁰С и давлении 100 кПа сжимается адиабатически до объема 13 л. Найдите температуру и давление газа после сжатия и затраченную при этом работу.

Р А З Д Е Л II

 

ЭЛЕКТРОМАГЕНТИЗМ

 

ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ

 

Физическая величина или закон	Формула
Закон Кулона (для точечных зарядов)
Напряженность электрического поля	E=F/q, где Е – напряженность электрического поля, F – сила, действующая на заряд q, помещенный в данное поле
Напряженность Е и потенциал φ поля, создаваемого точечным зарядом	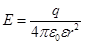, где– q – заряд, создающий поле, r – расстояние от заряда до заданной точки, электрическая постоянная, диэлектрическая проницаемость среды
Линейная плотность заряда	τ = q/l, τ = dq/dl, где τ – линейная плотность заряда, q – заряд, l – расстояние между зарядами
Поверхностная плотность заряда	σ=q/S, σ=dq/dS где σ – поверхностная плотность заряда, q – заряд, S – площадь поверхности
Объемная плотность заряда	ρ = q/V, ρ = dq/dV где ρ – объемная плотность заряда, q – заряд, V – некоторый объем
Поток вектора напряженности электрического поля	где dS – элемент площади поверхности, через которую определяется поток, α – угол между нормалью к данной поверхности и вектором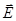
Теорема Гаусса
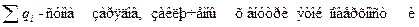
Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью
Напряженность Поля внутри конденсатора
Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром (нитью)
Работа сил поля по перемещению заряда q из точки поля с потенциалом φ1 в точку с потенциалом φ2	А12 = q (φ1-φ2), где А12 – работа сил по перемещению заряда, q – заряд, φ - потенциал
Электроемкость проводника	C=q/φ, где С – электроемкость проводника, q – заряд, φ - потенциал
Электроемкость плоского конденсатора	C = S/d, С=q/U, где C – электроемкость плоского конденсатора, электрическая постоянная, S – площадь конденсатора, d – расстояние между пластинами конденсатора, U – разность потенциалов, диэлектрическая проницаемость среды
Электроемкость батареи конденсаторов при последовательном соединении
Электроемкость батареи конденсаторов при параллельном соединении
Энергия заряженного конденсатора	W = qU/2, W=CU2/2, W=q2/(2C), где q – заряд конденсатора, U – разность потенциалов между обкладками, C – электроемкость конденсатора
Сила постоянного тока	I =q/t, I =dq/dt где I – сила тока, q – заряд, t - время
Плотность тока	j= I /S, где j – плотность тока, I – сила тока, S – площадь поперечного сечения проводника
Закон Ома для участка цепи, не содержащего ЭДС	, где I - сила тока, потенциал, U - напряжение, R - сопротивление
Закон Ома для участка цепи, содержащего ЭДС
Закон Ома для замкнутой (полной) цепи	, где I – сила тока, э.д.с., R – сопротивление, r – внутреннее сопротивление источника тока
Первый закон Кирхгофа
Второй закон Кирхгофа	где Ii Ri – падение напряжения в замкнутом контуре, - ЭДС в данном контуре
Сопротивление проводников при последовательном соединении
Сопротивление проводников при параллельном соединении
Мощность тока	Р= IU, P = I 2 R, P=U 2 /R, где Р – мощность тока, I – сила тока, R – сопротивление, U - напряжение
Закон Джоуля-Ленца	dQ = I 2 Rdt=IUdt, где dQ – тепло, выделяемое при нагревании проводника, I – сила тока, R – сопротивление, t – время, U - напряжение
Закон Ома и Джоуля-Ленца в дифференциальной форме	j=γE, ω= γE2 где j – плотность тока, γ – удельная электрическая проводимость, Е - напряженность электрического поля, ω – объемная плотность мощности
Связь магнитной индукции Вс напряженностью Н магнитного поля	B=mm0H, где В – магнитная индукция, Н – напряженность магнитного поля, μ – магнитная проницаемость среды, µ0 – магнитная постоянная
Закон Био-Савара-Лапласа	где индукция поля, µ - магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, вектор, равный по модулю длине проводника, – радиус-вектор, проведенный из проводника в точку поля, α – угол между векторами
Магнитная индукция прямого бесконечно длинного проводника с током	где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, r0 – расстояние от проводника с током до точки, в которой определяется индукция магнитного поля
Магнитная индукция поля в центре кругового проводника с током	где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, R – радиус проводника
Магнитная индукция поля внутри соленоида	где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, N – количество витков, l – длина соленоида
Энергия магнитного поля соленоида	где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, I – сила тока, N – количество витков, l – длина соленоида, S – площадка, через которую проходит магнитный поток, В – магнитная индукция, V – объем соленоида, Н – напряженность магнитного поля
Сила, действующая на провод с током в магнитном поле (закон Ампера)	F = I B l sin α, , где F – сила, I – сила тока, В – магнитная индукция, l – длина провода, α – угол между векторами
Магнитный момент плоского контура с током	, где I – сила тока, S – площадь контура, нормальный вектор
Сила Лоренца	F = q υ B sin α, где q – заряд, υ – скорость заряда, В – магнитная индукция, α – угол между векторами
Магнитный поток в случае однородного магнитного поля и плоской поверхности	Ф = B S cos α, Ф = Bn S, где Ф – магнитный поток, B - магнитная индукция, S – площадь поверхности, α – угол между векторами , Вn – проекция вектора на направление нормали к площадке S
Работа по перемещению проводника с током в магнитном поле	dA = IdФ, где A – работа по перемещению проводника, Ф – магнитный поток, I – сила тока
ЭДС индукции	, где ЭДС индукции, ψ – полный магнитный поток, t - время
ЭДС самоиндукции	, где ЭДС самоиндукции, L – индуктивность, I – сила тока, t - время
Индуктивность соленоида	L =V, где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, V – объем соленоида, n – плотность намотки
Экстратоки при замыкании и размыкании цепи	I0 – сила тока в начальный момент времени, R - активное сопротивление цепи, L - индуктивность
Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)	w = В2/(2 ), w = Н2/ 2, w = BН/ 2, где μ – магнитная проницаемость среды, μ0 – магнитная постоянная, B - магнитная индукция, Н – напряженность магнитного поля
Теорема Гаусса для электростатического поля в диэлектрике	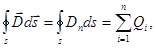где вектор электрического смещения, s – произвольная замкнутая поверхность, Dn – проекция вектора на нормаль к площадке s, алгебраическая сумма свободных зарядов, заключенных внутри данной замкнутой поверхности
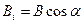Закон полного тока для магнитного поля	где вектор элементарной длины контура, ( угол между векторами ), вектор магнитной индукции, μ0 – магнитная постоянная, 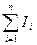— алгебраическая сумма токов, охватываемых контуром, n — число токов.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

 

Задача 1. Два точечных заряда 9 Q и -Q закреплены на расстоянии l = 50 см друг от друга. Третий заряд Q ₁может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q ₁, при котором он будет находиться в равновесии. При каком знаке заряда Q ₁равновесие будет устойчивым?

Решение. Заряд Q ₁находится в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Это значит, что на заряд Q ₁дол­жны действовать две силы, равные по модулю и проти­воположные по направлению. Рассмотрим, на каком из трех участков I, II, III (Рис. 4) может быть выполнено это условие. Для определенности будем считать, что заряд Q ₁— положительный.

Рис. 5.

На участке I (рис. 5, а) на заряд Q ₁будут дей­ствовать две противоположно направленные силы: и . Сила , действующая со стороны заряда 9 Q, в любой точке этого участка больше силы , действующей со стороны заряда

-Q, так как больший заряд 9Q находится всегда ближе к заряду Q _1, чем меньший (по модулю) заряд -Q. Поэтому равновесие на этом участке невозможно.

На участке II (рис. 4, б) обе силы и направ­лены в одну сторону — к заряду -Q. Следовательно, и на втором участке равновесие невозможно.

На участке III (рис. 4, в) силы и направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд -Q всегда нахо­дится ближе к заряду Q _1,чем больший заряд 9 Q. Это значит, что можно найти такую точку на прямой, где силы и будут одинаковы по модулю, т. е.

= (1)

Пусть х и l+х — расстояние от меньшего и боль­шего зарядов до заряда Q _1.Выражая в равенстве (1) и в соответствии с законом Кулона, получим

9 Q Q ₁(l + x) ² = Q Q ₁ /x ², или l + x = ± З х, откуда

x ₁ = + l/ 2,

x ₂ = - l/ 4.

Корень x ₂не удовлетворяет физическому условию задачи (в этой точке силы и хотя и равны по модулю, но сонаправлены).

Определим знак заряда Q ₁, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равно­весия. Рассмотрим смещение заряда Q ₁ в двух случаях: когда заряд положителен и когда отрицателен.

Если заряд Q ₁положителен, то при смещении его влево обе силы 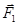и возрастают. Так как сила 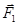воз­растает медленнее, то результирующая сила, действую­щая на заряд Q ₁, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд Q ₁ будет удаляться от положения равно­весия. То же происходит и при смещении заряда Q ₁вправо. Сила убывает быстрее, чем 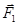. Геометриче­ская сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.

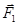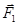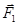Если заряд Q ₁отрицателен, то его смещение влево вызовет увеличение сил и , но сила возрастает медленнее, чем , т. е. | |>| |. Результирующая сила будет направлена вправо. Под ее действием заряд Q ₁ возвращается к положению равновесия. При смещении Q ₁ вправо сила убывает быстрее, чем 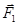, т. е. | 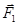|>| |. результирующая сила направлена влево и заряд Q ₁ опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q ₁несущественна.

 

Рис. 6.

 

Задача 2. Три точечных заряда Q ₁ = Q ₂ = Q ₃ = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q ₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равно­весии?

Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует по­местить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например Q _1,находился и равновесии. Заряд Q ₁ будет находиться в равновесии, если век­торная сумма действующих на него сил равна нулевому вектору (Рис. 6):

(1)
где , , — силы, с которыми соответственно дей­ствуют на заряд Q ₁ заряды Q ₂, Q _3, Q ₄; равнодей­ствующая сил и

Так как силы и направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F - F ₄ = 0, откуда F ₄ = F. Выразив в последнем равенстве F через F ₂, F ₃ и учиты­вая, что F ₃ = F ₂, получим

F ₄ = F ₂ .

Применив закон Кулона и имея в виду, что Q ₂ = Q ₃ = Q ₁, найдем

откуда Q ₄= (2)

Из геометрических построений в равностороннем тре­угольнике следует, что

, cos α=cos 60°=l/2.

С учетом этого формула (2) примет вид

Q ₄ = Q ₁ .

Произведем вычисления:

Q ₄ = 10^-9 / Кл = 5,77·10^-10 Кл = 577 пКл.

Задача 3. На тонком стержне длиной l = 20 см нахо­дится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд Q ₁ = 40 нКл, который взаимодействует со стержнем с си­лой F = 6 мкН. Определить линейную плотность τ заряда на стержне.

Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Q ₁зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ.

 

Рис. 7

 

При вычислении силы F следует иметь в виду, что заряд на стержне не является точеч­ным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (Рис. 7) малый участок dr с зарядом dQ = τdr. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,

d F =

Интегрируя это выражение в пределах от a до a + l, получаем

 

F =

 

откуда

Проверим, дает ли рас­четная формула единицу линейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подста­вим их единицы:

 

Найденная единица является единицей линейной плот­ности заряда.

Произведем вычисления:

 

Задача 4. Два точечных электрических заряда Q ₁ = 1 нКл и Q ₂= - 2 нКл находятся в воздухе на рас­стоянии d = 10 см друг от друга. Определить напря­женность 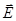и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q ₁на расстоя­ние r ₁= 9 см и от заряда Q ₂ на r ₂ = 7 см.

Решение. Согласно принципу суперпозиции элек­трических полей, поле, созданное зарядом, не зависит от присутствия других зарядов. Поэтому напряженность 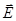электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей и полей, создаваемых каждым зарядом в отдельности: 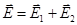. Напряженности электриче­ского поля, создаваемого в воздухе (ε = 1) зарядами Q ₁ и Q ₂, складываются.

Вектор (Рис. 8.) направлен по силовой линии от заряда Q ₁, так как этот заряд положителен; вектор направлен также по силовой линии, но к заряду Q ₂ так как этот заряд отрицателен.

 

Рис. 8.

Модули векторов и находим по формулам

, (1)

. (2)

Модуль результирующего вектора 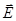найдем по теореме косинусов:

Е = (3)

где α - угол между векторами и , который может быть найден из треугольника со сторонами r ₁, r ₂и d: cos α = . В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:

cos α =

Подставляя выражение Е ₁ из (1) и Е ₂ из (2) в (3) и вынося общий множитель 1/(4 ) за знак корня, получаем

Е = (4)

В соответствии с принципом суперпозиции электриче­ских полей потенциал φ результирующего поля, созда­ваемого двумя зарядами Q ₁ и Q ₂, равен алгебраической сумме потенциалов;

(5)

Потенциал электрического поля, создаваемого в ва­кууме точечным зарядом Q на расстоянии r от него, выра­жается формулой

. (6)

В нашем случае согласно формулам (5) и (6) получим

+ ,

 

Произведем вычисления:

=3,58·10³ В/м = 3,58 кВ/м;

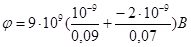=-157 В.

 

Рис. 9

Задача 5. По тон­кому кольцу равно­мерно распределен за­ряд Q = 40 нКл с ли­нейной плотностью τ = 50 нКл/м. Опреде­лить напряженность 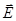электрического поля, создаваемого этим за­рядом в точке А, лежа­щей на оси кольца и удаленной от его цен­тра на расстояние, рав­ное половине радиуса.

Решение. Сов­местим координатную плоскость хoу с плоскостью кольца, а ось oz - с осью кольца (Рис. 9). На кольце выделим малый участок длиной dl. Так как заряд dQ = τ dl, находящийся на этом участке, можно считать точечным, то напряженность d 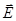электрического поля, создаваемого этим зарядом, может быть записана в виде

,

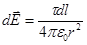где r — радиус-вектор, направленный от элемента dl к точке А.

Разложим вектор d 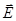на две составляющие: d 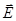₁, пер­пендикулярно плоскости кольца (сонаправленную с осью Oz), и d 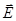₂, параллельную плоскости кольца (плос­кости хoу), т. е.

Напряженность Е электрического поля в точке А найдем интегрированием

,

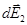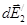где интегрирование ведется по всем элементам заряженно­го кольца. Заметим, что для каждой пары зарядов (dQ = dQ'), расположенных симметрично относительно центра кольца, векторы и в точке А равны по модулю и противоположны по направлению: .Поэтому векторная сумма (интеграл) .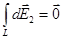

Составляющие для всех элементов кольца сонаправлены с осью oz (единичным вектором , определяющим направление оси Z), т.е. . Тогда

_.

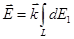Так как dE = 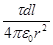, r = 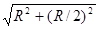= = и cos α = (R/2)/ r = l/ 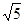, то

dE ₁ = = .

Таким образом

.

 

Из соотношения Q = 2 πRτ определим радиус кольца: R = Q /(2 πτ). Тогда

.

Модуль напряженности . (1)

Проверим, дает ли правая часть полученного равен­ства единицу напряженности (В/м):

Выразим физические величины, входящие в форму­лу (1), в единицах СИ () и произведем вычисления:

Е = В/м = 7,94 кВ/м.

Задача 6. Две концентрические проводящие сферы радиусами R ₁ = 6 см и R ₂ = 10 см несут соответственно заряды Q ₁ = 1 нКл и Q ₂ = -0,5 нКл. Найти напряжен­ность Е поля в точках, отстоящих от центра сфер на рас­стояниях r ₁= 5 см, r ₂ = 9 см, r ₃ = 15 см). Построить график Е (r).

Решение. Заметим, что точки, в кот