Ұғымдармен жүргізілетін жұмыстардың ішіндегі екінші бір логикалық амал - бөлу және жіктеу (классификациялау).
Оқушылардың логикалық ойлауын жетілдіруде ұғымдарды жіктеудің маңызы ерекше. Бөлу және жіктеу амалдарын жүзеге асыру нәтижесінде оқушылар ұғымдардың көлемі мен мазмұны, белгілері, тектік ұғымды көрсете алу және олардың түрлік ұғымдарын табу т. б. сияқты ұғымдармен жүргізілетін жұмыстарды меңгерсе, екінші жағынан жіктеу арқылы осы білімдерді тиянақтауға мүмкіндік туады.
Ұғымдарды түрлі топтарға бөлумен таныстыру ұғымдарды қалыптастыруда, есептер мен мысалдар шығаруда қажетті құрал болып табылады. Жіктеу оқушылардың танымдық қызметі үшін де маңызды. Тектік ұғымдарды түрлік бөліктерге бөлу арқылы, оны тереңірек және толық зерттеуге мүмкіндік туады. Мәселен, квадрат теңдеулерді шешуді үйрету барысында, оны толық, толымсыз және келтірілген түрлеріне ажырату арқылы оқушылардың квадрат теңдеу туралы толық түсінігі қалыптасады. Сол сияқты тригонометриялық теңдеулерді жай, біртекті, квадрат тендеулерге келтірілетін т. б. түрлерге жіктеу арқылы үйрету оқушылардың тригонометриялық теңдеулерді шешу дағдыларын берік қалыптастырады.
Сонымен математикалық ұғымдардың мазмұны мен көлемін ашу мақсатында оларды әр түрлі топтарға бөліп, әрқайсысын жеке-жеке ойлау объектісі ретінде қарастыруға тура келеді. Ұғымдарды анықтау амалы ұғымның мазмұнын ашатын болса, жіктеу - ұғымның көлемін анықтайды. Жіктеудің мақсаты ұғымға жататын оның барлық түрлерін көрсету.
Ұғымдарды қандай да бір белгілері бойынша бір-бірімен үйлеспейтін бөліктерге ажырату амалы бөлу деп түсініледі. Мұндағы бөлінетін ұғым - ұғымның тегі (немесе белінгіш ұғым), одан бөлініп алынғандары - түрлік ұғымдар (бөлу мүшелері) болады. Ұғымды бірнеше бөліктерге бөлетін белгісі бөлудің негізі деп аталынады. Бөлудің негізі түрлік ерекшелік болып табылады.
Ұғымдарды жіктеу үшін бөлу, жіктеу (немесе бөлу) негізі деген не, жіктеу кезінде қандай ережелерді басшылыққа алу керек т. б. мәселелерді айқын білуге тура келеді. Сонымен қатар ұғымдарды жіктеу оқушылардың белгілі бір іс-әрекеттер тізбегін орындауымен де сипатталады: 1) алдымен жіктеу негізі болатын, ұғымның қандай да бір белгілері таңдап алынады; 2) таңдап алынған негіз бойынша жіктеу ережелерін сақтай отырып, жіктеу жүзеге асырылады.
Егер үшбұрыштың бөлу негізіне оның бұрыштарын алатын болса, онда ол сүйір бұрышты, тікбұрышты, доғал бұрышты үшбұрыштарға, ал қабырғалары бойынша бөлетін болсақ - тең қабырғалы, тең бүйірлі, әр түрлі қабырғалы үшбұрыштар болар еді. Мұны сүлбе түрінде былай кескіндеуге болады (1- сурет):

1- сурет
Бөлудің ерекше түрі - жіктеу. Жіктеу ұғымының елеулі белгілері бойынша бөліктерге бөліп қоймастан, ол бөліктердің өзін тағы да майда бөлікшелерге ажыратады.
Үшбұрыш ұғымының бөлігі болатын тікбұрышты үшбұрышты тағы да екі қабырғасы тең болатын және екі қабырғасы тең болмайтын екі бөлікке бөлшектеуге болады. Тең бүйірлі үшбұрыш та екіге бөлінеді:тең бүйірлі тікбұрышты үшбұрыш, тең бүйірлі тікбұрышты емес үшбұрыш.
Жіктеудің мынадай құрамды бөліктері бар:
1) жіктеуші ұғымдар — көлемін ашуды қажет ететін ұғымдар;
2) жіктеу негізі — жіктеу жүргізілетін белгілер;
3) жіктеу мүшелері — жіктеу нәтижесінде пайда болатын ұғымдар.
Мәселен, V сыныпта жай бөлшектерді дұрыс және бұрыс бөлшектер деп екіге бөледі. Мұндағы жіктелетін ұғым — жай бөлшектер, жіктеудің негізіне бөлшектің алымы мен бөлімін салыстырудағы «кіші», «үлкен» немесе «тең» қатыстары жатады, жіктеу мүшелері — дұрыс және бұрыс бөлшектер.
Жіктеу арқылы тектік ұғым оған бағынышты түрлік ұғымдар жүйесіне жіктеледі.
Жіктеудің екі түрі бар: түрлік өзгерістегі белгілер бойынша жіктеу; дихтомиялық жіктеу.
2. Түрлік өвгерістегі белгілер бойынша жіктеу.
Ұғымдарды әр түрлі негіз бойынша жіктеуге болады, яғни бөлу негізі үшін ұғымның түрліше белгілері алынуы мүмкін. Ұғымдарды әр түрлі белгілеріне байланысты бөлу түрлік өзгерістегі белгілер бойынша (қысқаша түрлік өзгерістегі) жіктеу деп аталынады. Мысалы, алгебрада теңдеулерді дәреже көрсеткішіне байланысты бірінші дәрежелі, екінші дәрежелі, үшінші дәрежелі т. С. С. Жіктейді. Квадрат тендеулерді х -тің коэффициенті және бос мүшенін нөлге тең болу, болмауына қарай толык, және толымсыз квадрат тендеулер ажыратады. Егер теңдеулерді белгісіздердің санына байланысты жіктейтін болсақ, онда оларды бір белгісізі бар, екі белгісізі бар, үш белгісізі бар теңдеулер деп бөледі. Теңдеулер жүйесін сызықтық теңдеулер жүйесі, біреуі бірінші дәрежелі, ал екіншісі екінші дәрежелі тендеулер жүйесі т. Б. деп жіктеуге болады.
Түрлік өзгерістегі жіктеу, бір мезгілде ұғымның бірнеше белгісі бойынша да жүргізілуі мүмкін. Мысалы, екі белгісізі бар бірінші дәрежелі теңдеу, екі белгісізі бар екінші дәрежелі теңдеу т. Б,
Жіктеу негізін таңдап алу оқу материалының мазмұнына және қойылған мақсатқа байланысты болады. Жіктеудің мақсаты үшін функциялардың жұптығы алынатын болса, онда функцияларды жұп функциялар, тақ функциялар, жұп та тақ та емес функциялар деп ажыратады. Есеп шығару кезінде үшбұрыштардың бұрыштарын қарастыру қажет болса, онда сүйір, доғал, тікбұрышты үшбұрыштар деп жіктеуге тура келеді.
Ұғымдарды қандай жағдайда жіктейтін болсақ та жіктеу негізі объективті болу керек, мәселен есепті оңай немесе қиын деп бөлуге болмайды.
2. Дихтамиялық жіктеу. Дихтомиялық жіктеу бойынша ұғымдар бір-біріне қарама-қарсы (қайшылықта болатын) екі ұғымға ажыратылады. Ұғымдардың бірі қандай да бір белгіге ие болады да, екіншісінде ондай белгі болмайды. Дихтомия гректің dicha және tоте деген сөздері негізінде алынған, оның сөзбе-сөз мағынасы «екі бөлікке жару».
Дихтомиялық жіктеу бойынша сандар оң және теріс, жазықтықтағы түзулер қиылысатын және қиылыспайтын (параллель және параллель емес), теңдеулер сызықтық және сызықтық емес т.с.с. бола береді.
Дихтомиялық жіктеу ұғымдарды бірінен соң бірін бірнеше рет бөліктеуге мүмкіндік береді. Үшбұрыштардың тікбұрышының болу, болмауына қарай жіктеу мынадай түрде болады:

2-сурет
Ұғымдарды бірі екіншісіне қарама-қайшылықта болатын екі ұғымға жіктеу кезінде «емес» арқылы бөлінгенінің түрлі ұғымдары анықталмай қалады. Мысалы, тікбұрышты емес үшбұрыштың өзін не бұрыштарына, не қабырғаларына қатысты жіктеуге болады:

3-сурет.
Жіктеу арқылы ұғымдардың көлемі туралы толық мағлұмат алуға болады. Мысалы, мектеп математика курсындағы нақты сандар ұғымының жіктеуі мынадай:

4-сурет.
Бұл жіктеудің ішінде өз алдына бөлінетіндер болады.

5-сурет.
Мектептегі оқыту тәжірибесінде жіктеудің екі түрі де қолданылады. Алғаш жіктелетін ұғымның көлемі дихтомия негізінде бір-біріне қарама-қарсы екі түрлік ұғымға бөлінеді. Сонымен бір мезгілде кейбір ұғымдар түрлік өзгерістер бойынша жіктеліп жатады. Кейде жіктелудің екі түрі де бірінен сон бірі орындалады.
Дихтомиялық жіктеумен оқушылар бөлшек сандарды оқып үйренуде танысады. Бөлшектер жай және ондық бөлшектерге бөлінеді. Жай және ондық бөлшектердің өзі түрлік өзгерістер бойынша дұрыс, бұрыс және аралас бөлшектерге ажыратылады. Натурал сайдар жай және құрама, бір сандарына бөлінеді. Түзулер қиылысатын және қиылыспайтын болып жіктеледі.
Ұғымдарды жіктеу арқылы оқушылар ұғымның белгілерін дұрыс ұғынып, тектік және түрлік ерекшеліктердін, арақатынасын ажыратуға және берілген ұғымның жіктеу кезінде пайда болған бөліктерінің ұқсастықтары мен айырмашылықтарын айқын көруге мүмкіндік туады. Жіктеу мүшелерінің әрқайсысы түпкілікті қарастырылып зерттеледі. Мысалы, геометриялық фигураларды түрлендіруді оқып үйренуде оның екі нүкте ара қашықтығын сақтайтын және екі нүкте ара қашықтығын сақтамайтын түрлеріне ажыратады. Алдымен түрлендірулер кезінде екі нүктенің ара кашықтығың сақтайтын түрлері қозғалыс, оның ішінде остік және центрлік симметрия, параллель көшіру оқытылады. Одан соң түрлендірулер кезінде екі нүктенің ара қашықтығын сақтамайтын ұқсас түрлендірулер қарастырылады.
3.Жіктеу ережелері.
Логикалық жіктеу амалын оқушылардың ұғынуы онша қиынға түспейді. Себебі жіктеу мәселесімен мектептегі барлық пәндерді оқыту кезінде таныстырылады. Дегенмен ұғымдарды жіктеу кезінде оқушылардың қателесуіне жол бермеу үшін мұғалім төмендегідей талаптардың орындалуын қадағалап отыруы тиіс. Бұларды жіктеу ережелері деп те атайды.
— Жіктеу негізі бірыңгай болуы керек, яғни ұғымның белгілі бір ерекшелігі бойынша ғана жіктеледі. Мәселен, үшбұрыштарды не қабырғаларының, не бұрыштарының шамасына қарай бөледі. Үшбұрыштарды тікбұрышты, тең бүйірлі, сүйір бұрышты деп жіктеуге болмайды.
Мектеп тәжірибесінде параллелограмды тіктөртбұрыш және ромб деп жіктеу жиі кездеседі, ол да дұрыс емес. Оның себебі тіктөртбұрыштар параллелограмдар ішінен барлық бұрыштарының тікбұрышты болуына, ал ромб барлық қабырғаларының тең болуы бойынша бөлініп алынған. Демек, оларды бөлу негіздері әр түрлі.
Әрине, қандай да бір объектіні түрліше сүйеніп жіктеуге болады. Мұның бір заттың өзін түрліше көзқарас тұрғысынан зерттеуге болатындығы жағынан ғылыми және тәжірибелік маңызы бар. Мысалы, бір жіктеу жүйесінде квадратты тіктөртбұрыштың түрі, ал екіншісінде ромбының түрі ретінде қарастыруға болады. Мұндай жағдайлар есептер шығаруда пайдалы.
Кейде оқушылар көпжақтар призмаларға, пирамидаларға бөлінеді деп есептейді. Оның өзіндік себебі де бар: мектеп геометрия курсында көпжақтардын призмалар және пирамидалардан басқа түрлері қарастырылмайды (кейбір дұрыс көпжақтардан басқа). Аталған қателікті болдырмау максатында «Көпжақтар» тақырыбын оқыту кезінде мектеп геометрия курсында қарастырылмайтын, басқа да көпжақтардың түрлерімен нақтылы модельдер арқылы таныстырған жөн. Содан кейін мектепте оқылатын көпжақтарды әр түрлі негіздер бойынша жіктеудің жолдары көрсетіледі. Мысалы, көпжақтар дұрыс және дұрыс емес, призмалар және призма еместер т.б. деп бөлуге болатындығы айтылады.
2. Жіктеу элементтерінің бірі екіншісіне тиісті болмау керек, яғни олардың ортақ элементтері болмайды. Мысалы, натурал сандарды тақ және жай сандар деп бөлуге болмайды, себебі 7 саны әрі жай, әрі тақ сан.
3. Жіктеу ұғымның ең жақын тегі бойынша жүргізіледі. Мысалы, көпбұрыштарды төртбұрыш, параллелограмм, трапеция деген тізбекпен жіктеуге болмайды. Соңғы жағдай керісінше болуы мүмкін. Себебі параллелограмм ұғымының ең жақын тегі төртбұрыш болғанымен де, параллелограмм трапецияның ең жақын тегі бола алмайды.
Нақты сандарды иррационал, бүтін және бөлшек сандар деп бөлуге де болмайды. Себебі бүтін және бөлшек сандарға өтуден бұрын аралық рационал сандар ұғымы қарастырылмай отыр.
4. Жіктеу толық болу керек. Мәселен, рационал сандарды оң және теріс сандарға бөлу жеткіліксіз, себебі оған нөл саны енбей қалып отыр.
5. Жіктеу өлшемдес болуы керек. Бұл жіктелетін ұғым мен оның бөлшектері көлемінің дәл келуін білдіреді.
Ұғымдарды жіктеу нәтижесінде оқушылар мынадай мәселелерді айқын түсінуі тиіс:
— жіктеу ұғымының кандай да бір белгісі (жіктеу негізі) бойынша жүргізіледі;
— жіктеу негізін тандап алуға байланысты жіктеу түрліше
болады;
— жіктеу мүшелері бөліктенген кластардың біреуіне ғана тиісті болады, бір мезгілде екі класқа жатқызуға болмайды.
4. Ұғымдарды жіктеу дағдыларын қалыптастыруға арналған жаттығулар.
Мектептегі оқыту үрдісінде ұғымдарды қандай да бір белгілері бойынша бөліп қарастырғанмен, яғни жіктеу жүргізілгенімен «жіктеу» туралы ұғымы берілмейді, қандай ережелер бойынша жіктеліп отырғандығы туралы түсінік жасалынбайды. Оқу бағдарламасы бұл мәселелерді айқын емес түрде қалыптастыруды көздейді. Сондықтан жіктеу ұғымы туралы айқын болмаса да, дұрыс түсінік қалыптасуы үшін оқушылармен мақсатты жаттығулар орындалуы қажет. Мектеп оқулықтарында ондай жаттығулар өте аз.
Жіктеу ұғымын және оқушылардың жіктеу дағдыларын қалыптастыруға бағытталған мынадай жаттығулар үлгісін ұсынамыз:
1. Мына төртбұрыштардың ішінен:
а) Тіктөртбұрышты көрсет;
ә) Тіктөртбұрыш болмайтындарын көрсет;
б) Төртбұрыштардың ішінен тіктөртбұрыштарды қалай ажыратып алдың (6-сурет)?

6 – сурет.
2. Берілген төртбұрыштардың ішінен квадратгы және квадрат еместерін көрсет (7-сурет).
а) Төртбұрыштың барлық қабырғалары тең болса, ол квадрат бола ма?

7 – сурет.
ә) Төртбұрыштың барлық бұрыштары тік болса, ол квадрат бола ма?
б) Тіктөртбұрыштың барлық қабырғалары тең болса ше?
в) Қандай шарттар орындалғанда төртбұрыш квадрат болады?
3. Берілген бөлшектердің дұрыс және бұрыс бөлшектерін бөлек жаз.

4. Жай бөлшектер екі бөлікке дұрыс ажыратылған ба?
Дұрысбөлшектер: 
Бұрыс бөлшектер: 
5. Жай бөлшектерді және ондық бөлшектерді бөліп жаз. Оларды екі топқа бөлу себептерін айтып бер.

6. Мыңа сандарды екі топқа бөліп жаз:
1; 2; 3; 5; 6; 7; 12; 15; 18; 34; 36; 72.
а) 36 санының бөлгіштерін;
ә) 36 санының бөлгіштері еместерін.
7. Мына сандарды екі топқа бөл:
37; 45; 50; 58; 60; 125; 360; 900.
а) 5-ке бөлінетін сандар; ә) 5-ке бөлінбейтін сандар.
8. 6 санына еселі болатын және оған еселі болмайтын сандарды көрсет.
65; 6; 10; 12; 13; 18; 21; 24; 30; 32; 45; 48; 54.
9. а және b әріптерінің нөлге қатысына байланысты ах=b тендеуінің шешімдері қандай болады?
10. ах2 + bх + с =0 квадрат тендеуін b және с мәндерінін нөлге тең болуына байланысты қандай теңдеулер пайда болады? Олар қалай аталады? Әрқайсысына нақтылы мысалдар келтір.
11. ах2 + bх + с = 0 тендеуінің шешімдерін дискриминанттың нөлге қатысына байланысты жікте.
12. у = ах2 + bх + с функциясының сызбасы D -ның, және а -ның мәндеріне байланысты жіктелген. Осы жағдайлардың әрқайсысына нақты мысалдар келтір.

8-сурет.
13. Үшбұрыштар бұрыштарының шамасына қарай қалай жіктеледі? Бұл жіктеудің қандай түріне жатады?
14. Қабырғаларының шамасына қарай үшбұрыштарды жікте.
15. Төртбұрыштың мына түрдегі жіктеуі дұрыс па?

9-сурет.
Жіктеудің қандай ережелері сақталмай тұр? Мұндай жіктелу не үшін керек?
16. Кеңістіктегі екі түзудің өзара орналасуының мүмкін болатын жағдайларын қарастыр. Оларды жіктеудің негізіне қандай белгілер алынып отыр? Жіктеудің бұл түрі не деп аталады?
17. Кеңістікте түзу мен жазыктықтың өзара орналасу жағдайларын жіктеу барысында қандай белгілер негізге алынады? Жіктеудің бұл түрі не деп аталынады? Сәйкес кесте жасап, әрбір жағдайлар үшін нақты мысалдар келтір.
18. Элементар функциялардың жіктеуі төмендегі сызба түрінде берілген.
Бұлардың жіктеу негізі үшін қандай белгілер алынған? Әрбір функциялар үшін нақты мысалдар келтір.
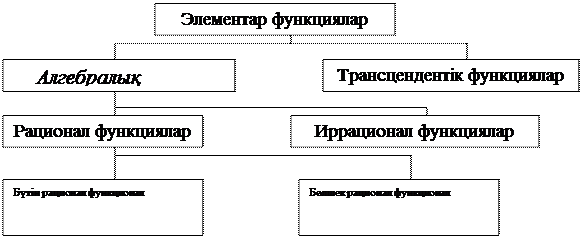
10-сурет.
19. Төмендегі ұғымдар тізбегінде жіктеу ережелері сақталып тұр ма? Сақталмаған жағдайда, қандай қателер бар?
а) Теңдеулер белгісіздің дәреже көрсеткішіне байланысты сызықтык (бірінші дәрежелі), (квадрат), (екінші дәрежелі) үшінші дәрежелі т.с.с. болып бөлінеді.
ә) Натурал сандар жұп және тақ сандар болып ажыратылады
б) Бүтін сандар оң және теріс сандар болып бөлінеді
в) Нақты сандар рационал, бүтін және натурал сандар болып ажыратылады.
г) Функциялар сызықтық, квадрат, жұп және тақ болып бөлінеді.
д) Параллелепипед тікбұрышты, тік, көлбеу параллелепипедтер болып жіктеледі.
Сұрақтар:
1.Математикалық ұғым;
2. Мазмұны мен көлемі;
3.Ұғымның тегі мен түрлік ерекшелігі қандай?
4. Математикалық ұғымдарды анықтау.
5.Ең жақын тегі және түрлік ерекшеліктері арқылы анықтау.
6.Генетикалық және аксиоматикалық щалай анықталады.
7.Математикалық ұғымды бөлу және жіктеме.




