Ұғымды тегі және түрлік ерекшеліктері бойынша анықтау үшін алдымен қандай да бір ұғым таңдалынады да, ол ұғымның белгілі бір ерекшелік бойынша одан басқа ұғым бөлініп алынады. Алғашқы ұғым тектік ұғым немесе ұғымның тегі, одан бөлініп алынған ұғым түрлік ұғым немесе анықталатын ұғым делінеді. Тектік ұғымнан түрлік ұғымды (анықталатын ұғымды) бөліп алатын белгі түрлік айырмашылық немесе түрлік ерекшелік деп аталынады. Мысалы, параллелограмның анықтамасы былай тұжырымдалады: “Параллелограмм деп қарама-қарсы қабырғалары параллель төртбұрышты айтады”. Бұл анықтамадағы тектік ұғымның аты – төртбұрыш, анықталатын ұғым параллелограмм, ал түрлік айырмашылық – қарама-қарсы қабырғалары параллель.
Мектеп математика курсында анықтамалардың көпшілігі “ұғымның тегі және түрлік белгілері (ерекшеліктері)” негізінде тұжырымдалады. Ондай анықтаманың құрылысы былай кескінделеді.
1. Анықталатын ұғым = түрлік ерекшелік + ұғымның тегі.
2. Түрлік ерекшелік + ұғымның тегі = анықталатын ұғым.
Анықтаманың құрылысы басқаша да болуы мүмкін. Анықтама қандай түрде тұжырымдалғанына қарамастан, оның құрамында анықталатын ұғым, ұғымның тегі және анықталатын ұғымды, оның тектік ұғымынан ажыратып тұратын түрлік белгілері болатындығын оқушы жақсы білуі тиіс. Сондықтан оқушы ұғымның анықтамасын айтудан бұрын мынадай екі нәрсені ой елегінен өткізіп алады:
1) Анықталатын ұғымның ең жақын тегі қандай?
2) Анықталатын ұғымды оның ең жақын тегінен бөліп тұратын түрлік ерекшелігі қандай?
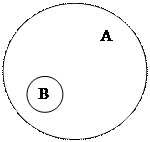Оқушылар анықталатын ұғым мен тектік ұғым арасындағы қатысты (байланысты айқын түсініп, көзге елестете алу үшін, дөңгелек диаграмма арқылы көрсету пайдалы. Мұндағы А – анықталатын ұғым, В – тектік ұғым. Диаграммадан көрінгендей тектік ұғым анықталатын ұғымды қамтып тұрады, басқаша айтқанда, анықталатын ұғым тектік ұғымның ішкі жиыны болады. Ұғымдарға анықтама беру, оның ең жақын тегі бойынша жүзеге асырылады. Мысалы, жоғарыдағы келтірілген анықтамада параллелограмның анықтамасы, оның ең жақын тегі төртбұрыш арқылы анықталған. Ұғымды тегі және түрлік ерекшелігі бойынша анықтау формальды логикалық анықтама деп аталынады. Мектеп математика курсында ұғымдар көбінесе ең жақын тегі мен түрлік ерекшеліктері арқылы анықталады. Анықтамада ұғымның тегі көрсетіледі, ал анықталатын ұғым, оның түрі ретінде енеді, онан соң жаңадан енгізілген ұғымды тектің басқа түрлерінен ерекшелейтін белгілері айтылады. Мысалы, тура пропорционалдықтың анықтамасы былай тұжырымдалады: “ 
(мұндағы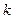 
нөлге тең емес сан) формуласы түріндегі функцияны тура пропорционалдық деп атайды”. Бұл анықтамада тектік ұғым “функция”, анықталатын ұғым “тура пропорционалдық”, түрлік ерекшелік – функцияның 
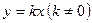түріндегі берілу мүмкіндігі.
2. Генетикалық анықтама ұғымның пайда болу жолын немесе тәсілін көрсету арқылы құрылады. Генетикалық анықтама да ұғымның тегін және түрлік ерекшелігін көрсетеді, бірақ түрлік ерекшелік ұғымның қалай пайда болатынын сипаттайды.
Генетикалық анықтама мынадай сүлбеде құрылады:
Анықталатын ұғым = ұғымның құрылу үрдісі + тегі.
Ұғымның құрылу үрдісі + тегі = анықталатын ұғым.
Мысалы, “Шеңбер деп берілген нүктеден бірдей қашықтықта жатқан жазықтық нүктелерінен тұратын фигураны айтады”. Бұл анықтамадағы анықталатын ұғым – шеңбер, түрлік ерекшелік немесе ұғымның құрылу жолы – бір нүктеден бірдей қашықтықтағы барлық нүктелер, тегі – фигура. “Екі жақты бұрыш деп ортақ бір түзумен шектелетін екі жарты жазықтықтан жасалған фигураны айтады”. “Пирамида дегеніміз – жазық көпбұрыштан, ол көпбұрыш жазықтығында жатпайтын нүктеден және сол нүктені көпбұрыштың нүктелерімен қосатын барлық кесінділерден тұратын көпжақ” т.б. анықтамалар генетикалық анықтаманың мысалдары болады.
Генетикалық анықтамалар алгебрада рекурентті анықтамалар түрінде де кездеседі. Мысалы, арифметикалық және геометриялық прогрессияның анықтамалары бірінші мүшесінен басқа әрбір мүшесін алдыңғы мүшеден алу тәсілі бойынша анықталады.
Математикада кейбір анықтамалар теңдік түріндегі символдық тілмен де беріледі. Мысалы:
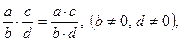
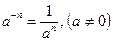
3. Жанамалай анықтау. Ұғымды жанамалай анықтауда ұғымның қасиеттері мен арақатыстары аксиома арқылы сипатталады. Мысалы, геометрия курсындағы “нүкте”, “түзу”, “жазықтық”, “ара қашықтық” сияқты алғашқы ұғымдардың қасиеттері мен арақатыстары аксиомалары арқылы ашылады.
Мектеп математика курсында анықтама берілмейтін ұғымдарға “сан”, “нүкте”, “жазықтық”, “түзу”, “кеңістік”, “уақыт”, “шама” т.б. жатады. Бұл ұғымдар материалдық дүниенің объектілерін абстракциялау жолымен алынған, сондықтан бұларды оқыту барысында көрнекілікке ерекше назар аударылады. Бірақ алғашқы ұғымдардың дұрыс қалыптасуын есепке алу мақсатымен “Сан деген не?”, “Нүкте деп нені айтамыз?” т.б. сұрақтар қоюдың мәні жоқ.
Оқушыларды анықтамаларды дұрыс тұжырымдауға үйрету үшін мынадай ережелер ескеріледі.
1. Анықтаманың өлшемдестігі. Бұл анықтамадағы елеулі белгілер анықталатын ұғымды басқа ұғымдардан айыру үшін қажетті және жеткілікті болу керек дегенді білдіреді.
