Внешний окружной модуль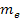 
конических зубчатых колес дифференциалов рекомендуется выбирать по аналогии конструкции дифференциалов современных транспортных машин. Для этих целей используются следующие формулы
;
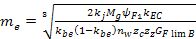; (1)
;
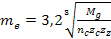где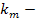 
эмпирический коэффициент, 
,
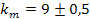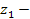число зубьев сателлита,
расчетный момент,
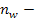число сателлитов,
,
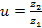где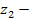 
число зубьев полуосевого зубчатого колеса.
Отношение 
к коническим дифференциалам составляет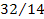 
, 
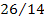и т.д.
Во всех случаях должно соблюдаться условие сборности
,
где 
целое число.
Все зубчатые колеса дифференциала прямозубые. Ширина зубчатого венца
,
где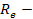 
внешнее конусное расстояние
.
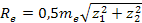Параметры исходного контура принимаются по ГОСТ 13754-88. Допускается использовать следующие параметры: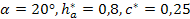 
. Коэффициенты смещения 
и 
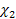принимаются равными по модулю, но для сателлита положительный, а для шестерни отрицательный.
При исходном контуре по ГОСТ принимают:
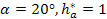, тогда 
,
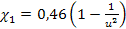при 
, тогда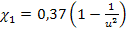 
.
В дифференциалах имеет место блокирование с помощью гидронажимных фрикционных муфт. Если фрикционная муфта блокирует полуось дифференциала, то момент трения муфты
,
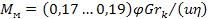где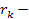 
расчетный радиус ведущего колеса,
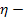КПД конической передачи.
По формуле (1)
число зубьев плоского колеса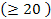 
, а для отв. передач 
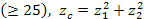при 90º. Соответствует контуру зубьев рейки.
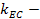коэффициент, учитывающий влияние двустороннего приложения нагрузки,
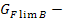предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжения,
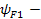коэффициент, учитывающий влияние формы зуба и концентрацию на изгиб,
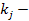коэффициент, учитывающий динамическую нагрузку,
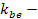коэффициент ширины зубчатого венца.
Для расчета полуосевых шестерен и сателлитов выбирается наибольший момент по сцеплению ведущих колес с дорожным покрытием.
,
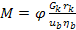где 
коэффициент сцепления,
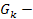нагрузка на ведущее колесо,
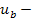передаточное число,
КПД бортовой конической передачи.
Момент, действующий на сателлит
.
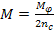Крестовина сателлита рассчитывается на срез от окружной силы
,
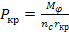где 
средний радиус действия окружной силы на крестовину.
,
,
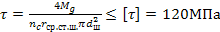где 
средний радиус поверхности контакта сателлита и шипа крестовины относительно оси полуосевых шестерен,
диаметр шипа крестовины,
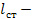длина цилиндрической поверхности сателлита под шип крестовины.
Вычисляют также напряжение смятия в контакте шипа крестовины с корпусом дифференциала
,
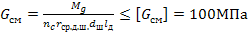где 
длина цилиндрической поверхности корпуса дифференциала под шип крестовины.
Зубчатые колеса крестовины и сухаря дифференциала изготавливают из высоколегированных сталей, применяемых для изготовления агрегатов трансмиссии, с цементацией на глубину 1,5…1,9 мм и закалкой до HRCэ от 58 до 63 с твердостью сердцевины от 30 до 40. Корпуса дифференциалов отливают из ковкого чугуна 35…10 или стали.
Определяют число зубьев сателлита по следующей формуле
,
где 
передаточное число от сателлита до полуосевой шестерни.
Обычно принимают в расчетах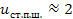 
, исходя из условия размещения полуосевых шестерен шлицевого конца полуоси нужного диаметра и ограничение размера дифференциала.
В дифференциале сателлитов от 2 до 4.
Полуоси
Полуоси служат для передачи крутящего момента от межосевого дифференциала к ведущим колесам машины и, по сути, являются ведущими валами. При зависимой подвеске колес полуоси располагаются внутри картера и, как правило, соединяются с полуосевыми шестернями дифференциала шлицами, а со ступицами ведущих колес с помощью шлицев или фланцев, составляющих одно целое с полуосями. Все типы полуосей рассчитываются на сопротивление усталости и статическую прочность, принимая в расчете, что балки не деформируются. В расчете принимают следующие действующие на полуось силовые факторы:
– в случае интенсивного разгона или торможения максимальный крутящий момент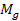 
и изгибающие моменты действуют по осям 
;
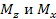– при заносе машины на повороте учитывают изгибающий момент относительно горизонтальной оси площадки;
– в случае переезда через препятствие учитывается изгибающий момент относительно горизонтальной оси к площадке опасного сечения полуоси.
Учитывают коэффициент динамичности, применяемый для высоконагруженных транспортных средств в пределах от 2 до 2,5, а для транспортных средств высокой проходимости от 2,5 до 3.
При расчете оценок статической прочности полуосей применяются дополнительные напряжения:
,
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>РІ</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
.
При этом эквивалентное напряжение, которое сравнивается с допускаемым, рассчитывается по следующим формулам
,
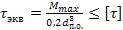где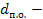 
диаметр полуоси в опасном сечении.
Для полуразгруженных и разгруженных на ¾ полуосей при интенсивном разгоне или торможении
,
где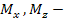 
изгибающие моменты относительно осе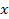й 
и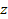 
.
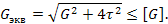
При заносе машины на повороте
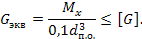
При переезде препятствия
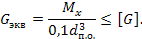
В существующих конструкциях диаметр полуосей у нагрузочных транспортных средств принимают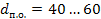 
мм.
Планетарные передачи
Основные соотношения планетарных механизмов.
Планетарным механизмом называют механизм, состоящий из зубчатых колес, в котором геометрическая ось хотя бы одного колеса подвижна. Зубчатое колесо с подвижной геометрической осью называется сателлитом. Сателлит может иметь один или несколько зубчатых венцов, либо состоять из находящихся в зацеплении нескольких колес.
Классификация трехзвенных планетарных механизмов
| Схема | Сателлиты | Зацепление | Значение периметра Р | |
| A |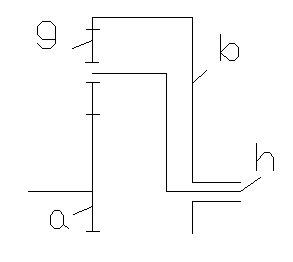 
| Одновен-цовые | Разнои-менные |
|
| B |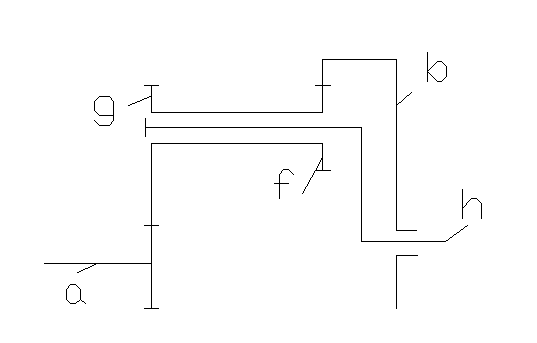 
| Двухвенцовые (блочные) | Разнои-менные |
|
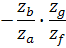
| D | 
| Одновен-цовые парные | Разнои-менные центра-льные |
|
Звено, в котором установлены оси сателлитов – водило (h). Зубчатое колесо, геометрическая ось которого совпадает с основной осью механизма – центральное(a,b,k). Основным звеном планетарного механизма называют звено, воспринимающее в нагруженной передаче внешний момент, и является центральным.
a – солнечная шестерня,
h – водило,
g – сателлит,
b – коронная шестерня (эпициклическая).
Планетарный механизм, у которого вращаются все 3 основных звена, называют дифференциалом. Планетарные механизмы обозначают по соответствию имеющихся сателлитов, зацеплений и значений параметров. Планетарные механизмы, в которых основными звеньями являются 2 центральных колеса и водило, обозначается 2k-h. Планетарный редуктор может состоять из одного планетарного механизма или нескольких, соединенных друг с другом. Классификация трехзвенных планетарных механизмов типа 2k-h приведена в классификации трехзвенных планетарных механизмов. Большее распространение в планетарных редукторах имеют трехзвенные планетарные механизмы типа A и D, значительно реже типа B. Кинематические и силовые характеристики трехзвенных планетарных механизмов определяются его кинематическим параметром r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
, равным передаточному числу от звена a к звену b при остановленном водиле h.
,
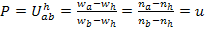где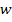 
и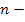 
угловая скорость и частота вращения звена соответственно.
Выражения для определения параметра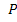 
с учетом знака указаны в таблице классификации трехзвенных планетарных механизмов. Приведенное уравнение параметра r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> известно как формула Виллиса и может быть непосредственно использована для расчета при анализе и синтезе планетарных редукторов, но удобнее использовать ее в преобразованном виде:
.
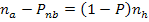Это уравнение часто называют основным уравнением кинематики трехзвенного механизма. В ряде случаев используют параметр k 
. При этом основное уравнение кинематики принимает следующий вид
.
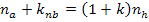Оценку схем планетарных редукторов производят по следующим показателям. Следует стремиться к тому, чтобы скорости на режиме длительной работы были не более 60 – 65 м/с и кратковременными в части работы элементов трехзвенных планетарных механизмов. Не рекомендуется иметь 
; 
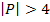. Желательно, чтобы значение параметров находилось в пределах 1,7…3. Для любого трехзвенного планетарного механизма имеется внутреннее передаточное число 
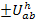от солнечной шестерни к коронной при остановленном водиле, которое называется параметром данного планетарного ряда. положительно, если оба элементарных зубчатых зацепления из планетарного ряда имеют одноименные зацепления (внутреннее или внешнее), а отрицательно при разноименных зацеплениях.
Силовой анализ планетарных редукторов
При силовом анализе планетарных редукторов используют следующие зависимости, пренебрегая силами трения.
;
;
.
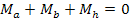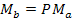На основании силового анализа решаются следующие задачи:
1. Определяют моменты на валу тягового электродвигателя, а затем переходят к определению показателей центральной передачи и планетарного редуктора.
2. Равенство момента на ведущем и ведомом валах планетарного механизма.
3. Находят моменты, нагружающие редуктор. Значение момента может быть положительно в результате решения уравнений, отражающих условие равновесия сателлита в зависимости между моментами на звеньях с блокирующим планетарным механизмом.
4. Равенство моментов с блокирующим механизмом.
5. Равенство суммы момента элементов планетарного редуктора, расположенных на его ведущем валу и момента на этом валу.
При проектировании передачи необходимо соблюдать условие сборки и соосности, тогда для передачи с внутренним зацеплением необходимо определить число зубьев солнечной шестерни, как наименьшее в ряду при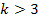 
(k 
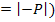и при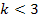 
определяют наименьшее число зубьев у сателлита.
Управляемый мост
