На всех рисунках: а) - фронтальная диметрическая проекция; б) - изометрия.
Рассмотрим более подробно построение правильного шестиугольника в изометрической проекции. Построение начинается с определения положения осей симметрии фигуры относительно осей координат той плоскости проекций, в которой лежит шестиугольник. Предположим, что два шестиугольника А и В (рис. 86,а) на ортогональном чертеже находятся в плоскости V и их оси симметрии располагаются параллельно осям О z и Ох.
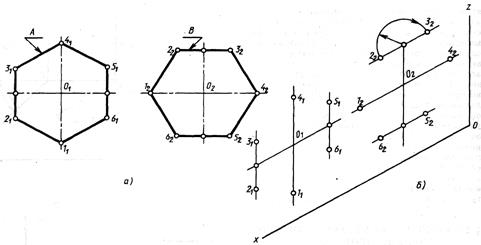
Рис.86
На рис. 87 построены шестиугольники в плоскостях Н, V и W.
|
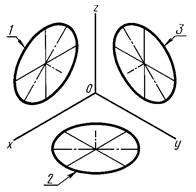Изображение окружности в прямоугольной изометрической проекции во всех трех плоскостях проекций представляет собой одинаковые по форме эллипсы (рис. 88).
Построение эллипсов требует применения лекал. Для простоты построения эллипсы заменяют овалом, который строится циркулем.
|
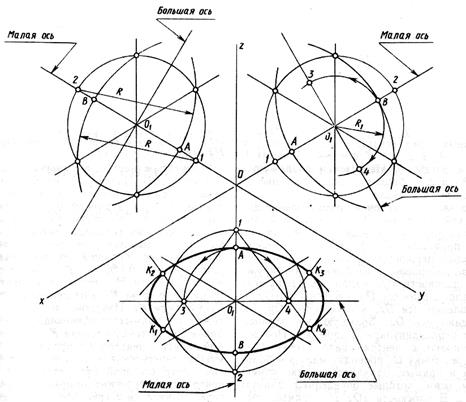
Существует несколько способов построения, рассмотрим один из них. Овал состоит из четырех сопрягающихся дуг: двух больших и двух малых. Для его построения необходимо определить четыре точки, через которые проходят большие дуги, и четыре центра дуг.
На рис. 89 показаны три случая расположения овала относительно аксонометрических осей. В плоскости хОу построение доведено до конца, в двух других плоскостях построение остановлено на определенном этапе.
Построение овала начинают с проведения через центр овала (точка О1) прямых, параллельных осям Ох и Оz для плоскости xOz; Оz и Oy для плоскости zOy; Ох и Oy для плоскости xOy. Затем проводят малую и большую оси овала.
Из центра О1 описывают окружность радиусом, равным радиусу изображаемой окружности. В пересечении окружности с проведенными параллельно аксонометрическим осям прямыми получают четыре точки, через которые пройдут большие дуги, а на прямой, на которой находится малая ось овала, получают точки 1 и 2, которые являются центрами больших дуг.
|
Радиус большой дуги R равен расстоянию от точки 1 или 2 до точек, в которых проведенная окружность пересекла прямые, параллельные аксонометрическим осям (рис. 89, плоскость xOz).
Дальнейшее построение овала (проведение малых дуг) показано на рис.89 в плоскости zOy. Проведя большие дуги, построили малую ось овала АВ. Из центра О1 радиусом, равным половине отрезка АВ, проводят дуги до пересечения с большой осью овала, получают точки 3 и 4. Эти точки будут центрами малых дуг овала. Нахождение точек сопряжения больших и малых дуг показано на рис. 89 в плоскости xOy.
Геометрические тела в ортогональных и аксонометрических проекциях
Многогранники
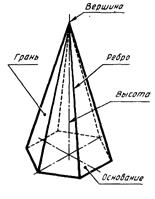Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником. К наиболее часто используемым в практике многогранникам относятся призма и пирамида.
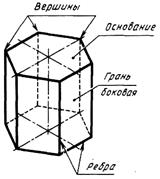
а) Рис. 90 б)
Призмой называется многогранник, основаниями которого являются многоугольники, а боковыми гранями - четырехугольники (прямоугольники или параллелограммы). Элементы призмы показаны на рис. 90,а.
Пирамидой называется многогранник, в основании которого лежит многоугольник, а боковые грани являются треугольниками, имеющими общую вершину. Элементы пирамиды показаны на рис. 90,б.
