И построение правильных вписанных многоугольников
Деление окружности на 3, 6 и 12 равных частей. Построение правильного вписанного треугольника, шестиугольника и двенадцатиугольника.
Для построения правильного вписанного треугольника надо из точки А пересечения центровой линии с окружностью отложить размер, равный радиусу R, в одну и другую сторону. Получим вершины 1 и 2(рис. 26, а). Вершина 3 лежит на противоположном точке А конце диаметра.



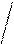


 1/3 1/6 1/12
1/3 1/6 1/12
а) б) в)
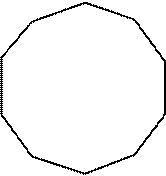
Рис. 26
Сторона шестиугольника равна радиусу окружности. Деление на 6 частей показано на рис. 26, б.
Для того чтобы разделить окружность на 12 частей, надо размер, равный радиусу, отложить на окружности в одну и другую сторону из четырех центров (рис. 26, в).
Деление окружности на 4 и 8 равных частей. Построение правильного
вписанного четырехугольника и восьмиугольника.


 1/8
1/8
 1/4
1/4
Рис. 27
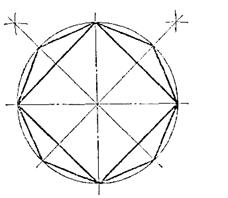
На 4 части окружность делится двумя взаимно перпендикулярными центровыми линиями. Для деления на 8 частей надо дугу, равную четверти окружности, разделить пополам (рис.27.)
Деление окружности на 5 и 10 равных частей. Построение правильного
вписанного пятиугольника и десятиугольника.
 1/5
1/5  1/10
1/10

 А
А


 | |||
 | |||

1/10
В
а) б)
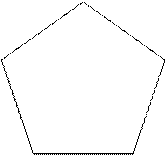
Рис. 28
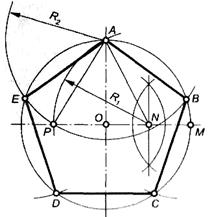
Половину любого диаметра (радиус) делят пополам (рис. 28, а), получают точку N. Из точки N, как из центра, проводят дугу радиусом R1, равным расстоянию от точки N до точки А, до пересечения со второй половиной этого диаметра, в точке Р. Отрезок АР равен хорде, стягивающей дугу, длина которой равна 1/5 длины окружности. Делая засечки на окружности радиусом R2, равным отрезку АР, делят окружность на пять равных частей. Начальную точку выбирают в зависимости от расположения пятиугольника. (! Нельзя выполнять засечки в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной.)
Деление окружности на 10 равных частей выполняют аналогично делению окружности на пять равных частей (рис. 28, б), но сначала делят окружность на пять частей, начиная построение из точки А, а затем из точки В, находящейся на противоположном конце диаметра. Можно использовать для построения отрезок ОР – длина которого равна хорде 1/10 длины окружности.
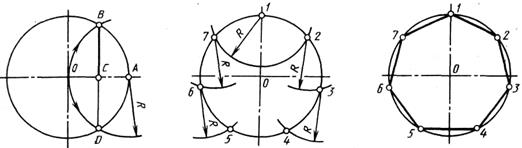 Деление окружности на 7 равных частей.
Деление окружности на 7 равных частей.
 1/7
1/7
 |
а) б) в)
Рис. 29
Из любой точки (например, А) окружности, радиусом заданной окружности рповодят дугу до пересечения с окружностью в точках В и D (рис. 29,а). Соединив точки В и D прямой, получают отрезок ВС, равный хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Засечки выполняют в последовательности, указанной на рис. 29 б.
Сопряжения
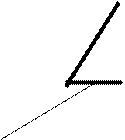
Часто в конструкции деталей одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. Сопряжение – это плавный переход от одной линии к другой. Построение сопряжений сводится к трем моментам: 1)определение центра сопряжения; 2)нахождение точек сопряжения; 3)построение дуги сопряжения заданного радиуса. Для построения сопряжения чаще всего задан радиус сопряжения. Центр и точка сопряжения определяются графически.
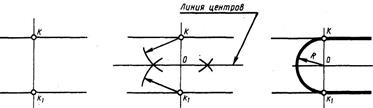
 На рис. 30,а приведен чертеж детали, при выполнении которого необходимо начертить различные сопряжения двух прямых. Пример выполнения сопряжения двух параллельных прямых дан на рис. 30,б; на рис. 30,в приведен пример выполнения сопряжения двух непараллельных прямых (под острым, тупым и прямым углами).
На рис. 30,а приведен чертеж детали, при выполнении которого необходимо начертить различные сопряжения двух прямых. Пример выполнения сопряжения двух параллельных прямых дан на рис. 30,б; на рис. 30,в приведен пример выполнения сопряжения двух непараллельных прямых (под острым, тупым и прямым углами).
 а) б)
а) б)
В) Рис. 30
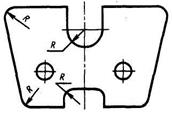
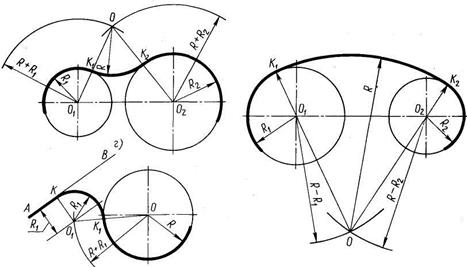 Примеры построения сопряжений между двумя окружностями по дуге заданного радиуса показаны на рис. 31.
Примеры построения сопряжений между двумя окружностями по дуге заданного радиуса показаны на рис. 31.
 а)
а)
б)
в)
Рис. 31 а) внешнее; б) внутреннее; в) между прямой и окружностью.






