Внешнее сопротивление R есть сумма двух сопротивлений 3 страница

Разность потенциалов на концах проводника, движущегося со скоростью 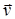в магнитном поле, U = Blv· sin a,

где l - длина провода; a - угол между векторам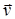и и .

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур: или , где R - сопротивление контура.

12. Индуктивность контура L = Ф / I.

Индуктивность соленоида L = mm₀ n ² lS,

где n - отношение числа витков соленоида к его длине; l – длина соленоида, S – площадь его поперечного сечения.

13. Э.д.с. самоиндукции

14. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

а) - при замыкании цепи, где e -э.д.с. источника тока; t - время, прошедшее после замыкания цепи;

б) - при размыкании цепи, где I ₀ - сила тока в цепи при t = 0; t - время, прошедшее с момента размыкания цепи.

15. Энергия магнитного поля соленоида W =

Объемная плотность энергии магнитного поля (отношение энергии поля к его объему)

w = BH /2 = B ²/(2mm₀) = mm₀ H ²/2.

 

4.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

№ 1. По отрезку прямого провода длиной l = 80 см течет ток I = 50 А. Определить магнитную индукцию поля, создаваемого этим током в точке А, равноудаленной от концов отрезка провода и находящейся на расстоянии r ₀ = 30 см от его середины.

Р е ш е н и е.

Для решения задачи воспользуемся законом Био-Савара-Лапласа

(1)

и принципом суперпозиции магнитных полей:

, (2)

где символ l означает, что интегрирование распространяется на всю длину провода, магнитная индукция, создаваемая элементом тока 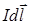в точке, определяемой радиус-вектором ; m ₀ - магнитная постоянная; m - магнитная проницаемость среды, в которой находится провод (в нашем случае m = 1). Векторы от различных элементов тока сонаправлены, поэтому выражения (1), (2) можно переписать в скалярной форме:

, ,

где a есть угол между вектором и радиус-вектором . Таким образом,

. (3)

Выразим длину элемента провода dl через угол d a: dl = rd a/sina.

Запишем выражение в виде Переменная r также зависит от a (r = r ₀/sina), следовательно: . Таким образом, выражение (2) можно переписать в виде , где a₁ и a₂ - пределы интегрирования.

Выполним интегрирование:

(4)

При симметричном расположении точки А относительно отрезка провода cos a₂ = -cos a₁. С учетом этого формула (4) примет вид

. (5)

Из рис.2 следует

Подставив выражение cosa₁ в формулу (5), получим

. (6)

Произведя вычисления по формуле (6), получим В = 26,7 мкТл.

№ 2. Два бесконечно длинных провода D и С, по которым текут в одном направлении токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию поля, создаваемого проводниками в точке А. (см. рис.), отстоящей от оси одного проводника на расстояние r ₁ = 5 см, от другого на r ₂ = 12 см.

 

Р е ш е н и е.

Для нахождения магнитной индукции в точке А воспользуемся принципом суперпозиции магнитных полей: = ₁+ ₂.

Модуль вектора может быть найден из теоремы косинусов

 

Рис. 3

, (1)

где a - угол между векторами ₁ и ₂.

Магнитные индукции ₁ и ₂ выражаются соответственно через силу тока I и расстояния r ₁ и r ₂ от проводов до точки А

В ₁ = m₀ I /(2p r ₁); B ₂ = m₀ I /(2p r ₂).

Подставляя выражения В ₁ и В ₂ в формулу (1), получаем

. (2)

Вычислим cos a по теореме косинусов (Ð a = Ð DAC как углы с соответственно перпендикулярными сторонами), d² = r ₁² + r ₂² - 2 r ₁ r₂ cos a,

где d - расстояние между проводами. Отсюда

Подставим в формулу (2) числовые значения физических величин и произведем вычисления:

= 308 мкТл.

 

№ 3. По тонкому проводящему кольцу радиусом R = 10 см течет ток I = 80 А. Найти магнитную индукцию в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см.

Р е ш е н и е.

Для решения задачи воспользуемся законом Био-Савара-Лапласа:

,

где d - магнитная индукция поля, создаваемого элементом тока I в точке, определяемой радиус-вектором .

Выделим на кольце элемент и от него в точку А проведем радиус-вектор (рис. 4). Вектор d направим в соответствии с правилом буравчика.

Согласно принципу суперпозиции магнитных полей, магнитная индукция в точке А определяется интегрированием: , где интегрирование ведется по всем элементам dl кольца.

Разложим вектор d на две составляющие: перпендикулярную плоскости

кольца d _^ и параллельную d _||, т.е. .Тогда ,

Рис. 4

из соображений симметрии, а векторы от различных элементов dl сонаправлены, следовательно , где dB _^ = dB cos b и dB = (поскольку перпендикулярен , то sin a = 1). Таким образом, , где cosb = R / r (см. рис 4). Окончательно получим: .

Выразим все величины в единицах СИ и произведем вычисления:

Вектор направлен по оси кольца в соответствии с правилом буравчика.

 

№ 4. Длинный провод с током I = 50 А изогнут под углом a = (2/3)p.. Определить магнитную индукцию в точке А (см. рис. 5). Расстояние d = 5 см.

 

 

Рис. 5

Рис. 5

Р е ш е н и е.

Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О (Рис. 5) В соответствии с принципом суперпозиции магнитных полей магнитная индукция в точке А будет равна геометрической сумме индукций ₁ и ₂ магнитных полей, создаваемых отрезками длинных проводов 1 и 2, т.е. = ₁ + ₂.

Магнитная индукция ₂ равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси провода, d = 0, т.к. [ d ]= 0.

Магнитную индукцию B ₁ найдем, воспользовавшись соотношением (4), из примера 1: где r ₀ - кратчайшее расстояние от провода 1 до точки А (см. рис. 5)

В нашем случае a ₁®0 (провод длинный), a ₂ = a = 2 p /3. Расстояние r ₀ = d sin(p - a). Тогда магнитная индукция .

Так как B =B ₁ (B ₂ = 0), то .

Вектор сонаправлен с вектором ₁ и направление его определяется правилом правого винта. На рис. 5 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас).

Произведем вычисления:

 

№ 5. Два бесконечно длинных провода скрещены под прямым углом (см. рис. 6) По проводам текут токи I ₁ = 80 A и I ₂ = 60 A. Расстояние d между проводами равно 10 см. Определить магнитную индукцию в точке А, одинаково удаленной от обоих проводов.

Р е ш е н и е.

В соответствии с принципом суперпозиции магнитных полей индукция магнитного поля, создаваемого токами I ₁ и I ₂, определяется

Рис. 6

выражением = ₁ + ₂, где ₁ - индукция магнитного поля, созданного в точке А током I ₁; ₂ - индукция магнитного поля, созданного в точке А током I ₂ (направление отмечено точкой в кружочке - перпендикулярно плоскости чертежа к нам).

Векторы ₁ и ₂, взаимно перпендикулярны, их направления находятся по правилу буравчика, и изображены в двух проекциях на рисунке. Модуль можно определить по теореме Пифагора (см. рис. 6)

,

В ₁ и В ₂ определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:

и .

В нашем случае r ₀ = d /2. Тогда .

Произведем вычисления: .

 

№ 6. Бесконечно длинный провод изогнут так, как изображено на рис.7. Радиус R дуги окружности равен 10 см. Определить индукцию магнитного поля, создаваемого в точке О током I = 80 А, текущим по этому проводу.

Р е ш е н и е.

Магнитную индукцию в точке О найдем, используя принцип суперпозиции магнитных полей: .

 

Рис. 7

В нашем случае провод можно разбить на три части (см. рис 7): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда , где , и - индукции магнитных полей в точке О, создаваемые током первого, второго и третьего участков провода.

Так как точка О лежит на оси провода 1, то = 0 и тогда = + . Учитывая, что векторы и направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, геометрическое суммирование можно заменить алгебраическим: В = В ₂ + В ₃.

Магнитную индукцию В ₂ найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока: .

В нашем случае магнитное поле в точке О создается лишь половиной кругового тока, поэтому .

Магнитную индукцию В ₃ найдем, применив соотношение (4), пример 1: .

В нашем случае r ₀ = R, a₁ = p/2 (cos a₁ = 0), a ₂ ®p (cos a₂ = -1). Тогда .

Используя найденные выражения, получим В = В ₂ + В ₃ = + ,

ли .

Произведем вычисления:

 

№ 7. По двум параллельным прямым проводам длиной l = 2 м каждый, находящихся на расстоянии d = 20 см друг от друга, текут одинаковые токи I = 1 кА. Вычислить силу взаимодействия токов.

Р е ш е н и е.

Взаимодействие двух проводов, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой провод.

Предположим, что оба тока (обозначим их I ₁ и I ₂) текут в одном направлении. Ток I ₁ создает в месте расположения второго провода (с током I ₂) магнитное поле, направление вектора магнитной индукции определяется по правилу буравчика. Модуль магнитной индукции В ₁ задается соотношением

. (1)

Согласно закону Ампера, на каждый элемент второго провода действует в магнитном поле сила . Так как вектор перпендикулярен вектору , то и тогда dF = I ₂ B ₁ dl. Подставив в это выражение значение В ₁, получим .

Силу F взаимодействия токов найдем интегрированием:

.

Учитывая, что I ₁= I ₂ = I, получим

.

Произведем вычисления:

Рис. 8

 

Сила сонаправлена с силой d , а направление d определяется правилом левой руки.

 

№ 8. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией В = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.

Р е ш е н и е.

Движение заряженной частицы в одно­родном магнитном поле будет происходить по окружности только в том случае, если частица влетит в магнитное поле перпендикулярно линиям индукции: . Так как сила Лоренца перпендикулярна вектору 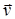, то она сообщает Рис. 9

частице (протону) нормальное ускорение _n.

Согласно второму закону Ньютона,

, (1)

 

где m - масса протона. На рис. 9 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора скорости 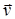. Силу Лоренца направим перпендикулярно вектору 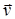к центру окружности (векторы _n и 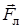сонаправлены.). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора ).

Перепишем выражение (1) в скалярной форме (в проекции на радиус):

F _л = ma _n. (2)

В скалярной форме F _л = qvB sin a. В нашем случае 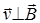и sin a = 1, тогда F _л = qvB. Так как нормальное ускорение a _n = v ²/ R, то выражение (2) перепишем следующим образом: qvB = m v ²/ R. Отсюда выразим радиус окружности:

R = mv / (qB). (3)

Скорость протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. А = D W, или q (j ₁ - j ₂) = W ₂ - W ₁, где (j₁ - j₂) = U - ускоряющая разность потенциалов (или ускоряющее напряжение); W ₁ и W ₂ - начальная и конечная кинетические энергии протона.

Пренебрегая начальной кинетической энергией протона W ₁» 0, и, учитывая, что W _к = mv ²/2, получим qU = mv ²/2.

Найдем из этого выражения скорость и подставим ее в формулу (3), в результате получим

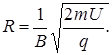(4)

Произведем вычисления:

 

№ 9. Электрон, влетев в однородное магнитное поле(В = 0,2 Тл), стал двигаться по окружности радиуса R = 5 см. Определить магнитный момент р _m эквивалентного кругового тока.

Р е ш е н и е.

Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции.

Движение электрона по окружности эквивалентно току, который в данном случае определяется выражением: где е - заряд электрона; Т - период его обращения.

Период обращения можно найти через скорость электрона и путь, проходимый электроном за период Т = (2 pR)/ v. Тогда

(1)