Внешнее сопротивление R есть сумма двух сопротивлений 2 страница

321. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = σ и σ₂ = -σ, где σ = 0,1 мкКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния от центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r = 3R и указать направление вектора .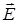

322. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ₁ = 2σ и σ₂ = σ, где σ= 20 нКл/м. Требуется: 1) найти напряженность Е электрического поля в трех областях: слева от плоскостей, между плоскостями и справа от плоскостей; 2) на чертеже указать направление вектора 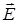для каждой области.

323. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями σ₁ = σ, σ₂ = -2σ, где σ = 20 нКл/м². Требуется: 1) найти напряженность Е электрического поля в трех областях: слева, между и справа от плоскостей, 2) на чертеже указать направление вектора 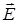для каждой области.

324. На двух концентрических сферах радиусами R и. 2R равномерно распределены заряды с поверхностными плотностями σ₁ = 4σ и σ₂ = σ, где σ = 30 нКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r = 1,5 R и указать направление вектора .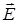

325. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -2σ и σ₂ = σ, где σ = 50 нКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до оси цилиндров для трех областей: внутри, между и вне цилиндров; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r = 1,5 R и указать направление вектора .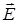

326. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -4σ и σ₂ = σ, где σ = 50 нКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r = 1,5 R и указать направление вектора .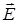

327. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = σ и σ₂ = -σ, где σ = 60 мкКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до оси цилиндров для трех областей: внутри, между и вне цилиндров; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r = 3R, и указать направление вектора .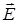

328. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -σ и σ₂ = 4σ, где σ = 30 НКл/м². Требуется: 1) найти зависимость Е(r) напряженности электрического поля от расстояния до оси цилиндров для трех областей: внутри, между и вне цилиндров; 2)вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r = 4R, и указать направление вектора .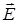

329. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями σ₁ = -2σ и σ₂ = σ, где σ = 0,1 мкКл/м². Требуется: 1) найти зависимость напряженности электрического поля от расстояния до центра сфер для трех областей: внутри сфер, между сферами и вне сфер; 2) вычислить напряженность Е в точке, удаленной от центра на расстоянии r = 3R, и указать направление вектора .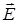

330. Четыре одинаковые капли ртути, заряженные до потенциала φ₁ = 10 В, сливаются в одну. Каков потенциал φ образовавшейся капли?

331. В однородное электрическое поле напряженностью Е = 200 В/м влетает вдоль силовых линий электрон со скоростью v₀ = 2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

332. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (τ = 10 нКл/м). Определить кинетическую энергию W_к2 электрона на расстоянии а, если на расстоянии 3а от линии его кинетическая энергия W_к1 = 200 эВ.

333. Шарик массой m = 40 мг, имеющий положительный заряд q = 1 нКл, движется со скоростью v = 10 см/с. На какое расстояние минимальное r может приблизиться шарик к положительному точечному заряду q₀ = 1,33 нКл?

334. Шарик массой m = 1 г и зарядом q = 10 нКл перемещается из точки 1, потенциал которой φ₁ = 600 В, в точку 2, потенциал которой φ₂ = 0. Найти его скорость в точке 1, если в точке 2 она стала равной v₂ = 20 см/с.

335. Найти скорость электрона, прошедшего разность потенциалов U, равную 100 В.

336. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом φ₁ = 100 В электрон имел скорость v₁ = 6 Мм/с. Определить потенциал φ ₂ точки поля, дойдя до которой электрон потеряет половину своей скорости.

337. Найти отношение скоростей ионов Cu ⁺⁺ и К ⁺, прошедших одинаковую разность потенциалов.

338. Электрон с энергией W = 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = -10 нКл.

339. Электрическое поле создано заряженным проводящим шаром, потенциал φ которого 300 В. Определить работу сил поля по перемещению заряда q = 0,2 мкКл из точки, отстоящей от поверхности шара на расстоянии R, до точки, отстоящей на расстоянии 3R.

340. Конденсатор электроемкостью С₁ = 0,6 мкФ был заряжен до разности потенциалов U₁ = 300 В и соединен параллельно со вторым конденсатором электроемкостью C₂ = 0,4 мкФ, заряженным до разности потенциалов U₂ = 160 В. Найти заряд, перетекший с пластин первого конденсатора на второй.

341. Конденсатор электроемкостью С₁ = 0,2 мкФ был заряжен до разности потенциалов U₁ = 320 В. После того, как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂ = 450 В, напряжение на нем изменилось до 400 В. Вычислить емкость С₂ второго конденсатора.

342. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка (ε = 7). Конденсатор заряжен до разности потенциалов U = 100 В. Какова будет разность потенциалов, если вытащить стеклянную пластинку из конденсатора?

343. К воздушному конденсатору, заряженному до разности потенциалов U ₁ = 500 В и отключенному от источника напряжения, присоединили параллельно второй конденсатор таких же размеров и формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость стекла ε, если после присоединения второго конденсатора разность потенциалов уменьшилась до U ₂ = 70 В

344. Два конденсатора емкостями С₁ = 5 мкФ и С₂ = 8 мкФ соединены последовательно и присоединены к батарее с э.д.с. ε = 80 В. Определить заряды q ₁ и q ₂ конденсаторов и разности потенциалов U ₁ и U ₂ между их обкладками.

345. Пластины плоского конденсатора изолированы друг от друга слоем диэлектрика. Конденсатор заряжен до разности потенциалов U = 1 кВ и отключен от источника напряжения. Определить диэлектрическую проницаемость диэлектрика, если при его удалении разность потенциалов между пластинами конденсатора возрастет до 3 кВ.

346. Три конденсатора (С ₁ = 1 мкФ, С₂ = 2 мкФ, С ₃ = 3 мкФ) соединены последовательно и присоединены к источнику напряжения (U = 220 В). Найти заряд и напряжение на каждом конденсаторе.

347. Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

348. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: стекла толщиной d ₁ = 0,2 см и парафина толщиной d ₂ = 0,3 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.

349. Два шара, радиусы которых 5 и 8 см, а потенциалы соответственно 120 и 50 В, соединяют проводом. Найти потенциалы шаров после их соединения и заряд, перешедший с одного шара на другой.

350. Плоский конденсатор с площадью пластин S = 300 см² каждая заряжен до разности потенциалов U = 10³ В. Расстояние между пластинами d = 4 см. Диэлектрик – стекло (ε = 7). Какую нужно совершить работу, чтобы удалить стекло из конденсатора? Конденсатор отключен от источника.

351. Энергия плоского воздушного конденсатора W ₁ = 2·10^-7 Дж. Определить энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если конденсатор отключен от источника питания.

352. Энергия плоского воздушного конденсатора W ₁ = 4·10^-7 Дж. Определить энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 4, если конденсатор подключен к источнику питания.

353. Пластины плоского конденсатора подключены к источнику с э.д.с 2 В. Определить изменение энергии электрического поля конденсатора, если конденсатор наполовину заполнить диэлектриком с диэлектрической проницаемостью ε = 2. Граница между диэлектриком и воздухом расположена перпендикулярно пластинам. Расстояние между пластинами d = 1 см, площадь пластин S = 50 см².

354. Пластины плоского конденсатора подключены к источнику с э.д.с 2 В. Определить изменение энергии электрического поля конденсатора, если конденсатор наполовину заполнить диэлектриком с диэлектрической проницаемостью ε = 2. Граница между диэлектриком и воздухом расположена параллельно пластинам конденсатора. Расстояние между пластинами d = 1 см, площадь пластин S = 50 см².

355. Разность потенциалов между пластинами плоского конденсатора 100 В. Площадь каждой пластины 200 см², расстояние между пластинами 0,5 мм, пространство между ними заполнено парафином (ε = 2). Определить силу притяжения пластин друг к другу и энергию поля конденсатора.

356. Плоский конденсатор заполнен диэлектрикоми на егопластины подана некоторая разность потенциалов. Его энергия при этом равна 2·10^-5 Дж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна 7·10^-5 Дж. Найти диэлектрическую проницаемость диэлектрика.

357. Плоский воздушный конденсатор с площадью пластин 100 см² и расстоянием, между ними 1мм заряжен до 100 В. Затем пластины раздвигаются до расстояния 25 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением: 1) не отключается; 2) отключается.

358. Пять параллельно соединенных одинаковых конденсаторов емкостью по 0,1 мкФ заряжаются до общей разности потенциалов U = 30 кВ. Определить среднюю мощность разряда, если батарея разряжается за τ = 1,5·10^-6 с. Остаточное напряжение равно 0,5 кВ.

359. Плоский воздушный конденсатор с площадью пластины S = 400 см² подключен к источнику тока, э.д.с. которого равна 200 В. определить работу внешних сил по раздвижению пластин от расстояния d ₁ = 2 см до d ₂ = 4 см. Пластины в процессе раздвижения остаются подключенными к источнику.

360. Э.д.с. батареи 12 В, сила тока короткого замыкания 5 А. Какую наибольшую мощность можно получить во внешней цепи, соединенной с такой батареей?

361. Э.д.с. батареи ε = 80 В, внутреннее сопротивление r₁ = 5 Ом. Внешняя цепь потребляет мощность Р = 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее сопротивление R.

362. Обмотка катушки из медной проволоки при t₁ = 14 ºС имеет сопротивление R ₁ = 10 Ом. После пропускания тока сопротивление обмотки стало равным R ₂ = 12,2 Ом. До какой температуры t ₂ нагрелась обмотка? Температурный коэффициент сопротивления меди α = 4,15·10^-3 К^-1.

363. В сеть с напряжением U = 100 В подключили катушку с сопротивлением R ₁ = 2 кОм и вольтметр, соединенные последовательно. Показание вольтметра U = 80 В. Когда катушку заменили другой, вольтметр показал U ₂ = 60 В. Определить сопротивление R ₂ другой катушки.

364. Э.д.с. батареи ε = 24 В, внутреннее сопротивление r = 2,4 Ом. Определить максимальную мощность Р_max, которая может выделяться во внешней цепи.

365. При внешнем сопротивлении R ₁ = 8 Ом сила тока в цепи I₁ = 0,8 А, при сопротивлении R₂ = 15 Ом сила тока I ₂ = 0,5 А. Определить силу тока I_кз короткого замыкания источника э.д.с.

366. Элемент, имеющий э.д.с. ε = 1,1 В и внутреннее сопротивление r = 1 Ом, замкнут на внешнее сопротивление R = 9 Ом. Найти ток I в цепи, падение потенциала U во внешней цепи и падение потенциала U_r внутри элемента. С каким к.п.д. η работает элемент?

367. Пять последовательно соединенных источников с э.д.с. ε = 1,2 В и внутренним сопротивлением 0,2 Ом каждый замкнуты на внешнее сопротивление R. Какой величины должно быть R, чтобы во внешней цепи выделялась максимальная мощность?

368. Сопротивление гальванометра R_Г = 720 Ом, шкала его рассчитана на 300 мкА. Как и какое добавочное сопротивление нужно подключить, чтобы можно было систему включать в цепь с напряжением 300 В?

369. Сопротивление гальванометра R_Г = 680 Ом. Какое сопротивление (шунт) нужно подключить к нему, чтобы можно было измерить ток силой 2,5 А? Шкала гальванометра рассчитана на 300 мкА.

370. Сила тока в проводнике равномерно убывает от 20 А до 6 А в течение 6 с. Какой заряд проходит через поперечное течение проводника за последние четыре секунды?

371. Определить напряженность электрического поля в алюминиевом проводнике объемом 10 см³, если при прохождении по нему постоянного тока за время 5 мин выделилось количество теплоты 2,3 кДж. Удельное сопротивление алюминия ρ = 26 нОм×м.

372. Сила тока в проводнике равномерно нарастает от I ₀ = 0 до I = 5 А в течение времени 10 с. Определить заряд, прошедший по проводнику.

373. Определить количество теплоты Q, выделившееся за время t = 10 с в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I ₁ = 10 А до I ₂ = 0.

374. За время t = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, прошедший в проводнике, если сила тока в начальный момент времени равна нулю.

375. За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимального значения в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока <I> в проводнике, если его сопротивление R = 26 Ом.

376. Плотность электрического тока в медном проводе равна 10 А/см². Определить объемную плотность тепловой мощности тока, если удельное сопротивление меди ρ = 17 нОм×м.

377. В проводнике за время t = 10 с при равномерном возрастании силы тока от I₁ = 1 А до I₂ = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.

378. Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I₁ = 5 А до I₂ = 10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.

379. За время t = 20 с при силе тока, равномерно возрастающей от нуля до некоторого максимума, в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока.

380. В схеме на рис. ε ₁ = 2 В, ε ₂ = 4 В, R₁ =0,5 Ом и падение потенциала на сопротивлении R₂ (ток через R ₂ направлен сверху вниз) равно 1 В. Найти показание амперметра. Внутренним сопротивлением элементов и амперметра пренебречь.

381. В схеме на рис. справа ε ₁ = 30 В, ε ₂ = 5 В, R ₂ = 10 Ом, R ₃ = 20 Ом. Через амперметр идет ток в 1 А, направленный от R₃ к R₁. Найти сопротивление R ₁. Сопротивлением батареи и амперметра пренебречь.

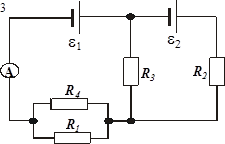382. В схеме на рис. ε₁ = ε₂ = 100 В, R₁ = 20 Ом, R₂ = 10 Ом, R₃ = 40 Ом, R₄ = 30 Ом. Найти показание амперметра. Сопро­тив­ле­нием батарей и ампер­метра пренебречь.

383. В схеме на рис. ε₁ =ε₂, R₂ = 2 R₁. Во сколько раз ток, текущий через вольтметр, больше тока, текущего через R₂? Сопротивлением генераторов пренебречь.

384. В схеме на рис. ε₁ = ε₂ = 110 В, R₁ = 200 Ом, сопротивление вольтметра 1000 Ом. Найти показание вольтметра. Сопротивлением батареи пренебречь. R₂ = 100 Ом.

385. Какую силу тока показывает миллиамперметр мА в схеме на рис., если ε₁ = 2 В, ε₂ = 1 В, R₁ = 10³ Oм, R₂ = 500 Ом, R₃ = 200 Ом и сопротивление амперметра равно R_А = 200 Ом? Внутренним сопротивлением элементов пренебречь.

 

386. Два элемента с одина­ковы­ми э.д.с. ε₁ = ε₂ = 2 В и внутренними сопротивлениями r₁ = 1 Ом и r₂ = 2 Ом замкнуты на внешнее сопротивление R (см. рис.). Через элемент с э.д.с. ε₁ течет ток I₁ = 1 А. Найти сопротивление R и ток I₂, текущий через элемент с э.д.с. ε₂. Какой ток I течет через сопротивление R?

387. К двум батареям, соединенным параллельно, подключили электролампу, сопротивление которой 0,5 Ом, э.д.с. батареи ε₁ = 12 В, ε₂-= 10 В и их внутреннее сопротивление r₁ = r₂ = 1 Ом. Найти ток, протекающий через лампу.

388. В схеме на рис. ε₁ = 2,1 В, ε₂ = 1,9 В, R₁ = 10 Ом, R₂ = 10 Ом и R₃ = 45 Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь.

 

389. В схеме на рис. ε₁ = 2 В, ε₂= 4 В, ε₃ = 6 В, R₁ = 4 Ом, R₂ = 6 Ом и R₃ = 8 Ом. Найти силу тока во всех участках цепи. Сопротивлением элементов пренебречь.

 

4. ОСНОВНЫЕ ФОРМУЛЫ

 

Электромагнетизм

1. Связь магнитной индукции с напряженностью магнитного поля.

,

где m - магнитная проницаемость однородной среды; m ₀ - магнитная постоянная. В вакууме m = 1, и магнитная индукция в вакууме

.

2. Закон Био-Савара-Лапласа

или

где - магнитная индукция поля, создаваемого элементом провода длиной c током I; - радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; a - угол между радиус-вектором и направлением тока в элементе провода.

3. Принцип суперпозиции магнитных полей

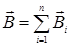или

для , созданных элементом тока .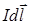

Направление вектора магнитной индукции поля, создаваемого прямым током, определяется по правилу буравчика (правого винта). Для этого проводим магнитную силовую линию (штриховая линия на рис.) и по касательной к ней в интересующей нас точке проводим вектор . Вектор магнитной индукции в точке А направлен перпендикулярно плоскости чертежа от нас.

Рис. 1

4. Магнитная индукция в центре кругового тока

где R - радиус кругового витка.

Магнитная индукция на оси кругового тока

где h - расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (вывод этой формулы в примере № 1):

Магнитная индукция поля, создаваемого бесконечно длинным прямолинейным проводником с током:

где r ₀ - расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля бесконечно длинного соленоида

B = mm₀ nI,

где n - отношение числа витков соленоида N к его длине l.

5. Сила, действующая на элемент провода с током в магнитном поле (закон Ампера):

,

где - вектор, равный по модулю длине участка провода и совпадающий по направлению с током; a - угол между направлением тока в проводе и вектором магнитной индукции .

Для однородного магнитного поля и прямого отрезка провода получим:

.

6. Магнитный момент плоского контура с током

,

где - единичный вектор нормали (положительной) к плоскости контура; I - сила тока, протекающего по контуру; S - площадь контура.

7. Механический вращающий момент, действующий на контур с током, помещенный в однородное магнитное поле:

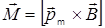или ,

где a - угол между векторами

8. Сила Лоренца

или ,

где 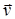- скорость заряженной частицы; a - угол между векторам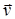и и .

Если частица находится одновременно в электрическом и магнитном полях, то на нее действует сила

.

9. Магнитный поток (через поверхность S):

а) в случае однородного магнитного поля и плоской поверхности

Ф = BS cos a или Ф = B _n S,

где S - площадь контура; a - угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

(интегрирование ведется по всей поверхности).

Потокосцепление (полный поток) – Y = NФ.

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

10. Работа по перемещению замкнутого контура с током в магнитном поле dA=I dФ или А=I×DФ.

11. Основной закон электромагнитной индукции (закон Фарадея-Максвелла): .