где f(t) – некоторая функция времени.

Перемещение материальной точки

,

где - ее радиусы – векторы в начальном и конечном положениях,

соответственно.

Пройденный путь – длина траектории.

2. Вектор средней скорости

.

Средняя скорость при движении вдоль оси х

< v _x> =

Средняя путевая скорость (скорость вдоль траектории)

< v > =

где D S – путь,пройденный точкой за интервал времени D t.

Мгновенная скорость

,

v _x =

3. Среднее ускорение

,

< a _x> =

Мгновенное ускорение

,

a _x =

4. При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих

.

Абсолютное значение этих ускорений

а _n = v²/R; a _τ = d v /d t; ,

где R – радиус кривизны в данной точке траектории.

5. Кинематическое уравнение равномерного движения материальной точки вдоль оси х (v = const, a = 0)

х = х ₀ + vt,

где х ₀ – начальная координата, t – время.

6. Кинематическое уравнение равнопеременного движения вдоль оси х (а = const)

x = x ₀ + v ₀ t + at ²/2,

где v ₀ – начальная скорость, t – время.

Скорость точки при равнопеременном движении

v = v ₀ + at.

7. Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) 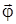. Кинематическое уравнение вращательного движения:

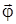= f (t).

Угловая скорость

=

Угловое ускорение

=

Угловое перемещение, угловая скорость и угловое ускорение являются псевдовекторами, их направления совпадают с осью вращения и определяются по правилу правого винта.

8. Кинематическое уравнение равномерного вращения (ω = const, ε = 0)

φ = φ ₀ +ω t,

где φ ₀ – начальное угловое перемещение; t – время.

9. Т - период вращения (время одного полного оборота)

Т = t /N;

ν – частота вращения (число оборотов в единицу времени)

ν = N / T или ν = 1/ Т,

где N – число оборотов, совершаемых телом за время t,

ω = .

10. Кинематическое уравнение равнопеременного вращения (ε = const)

φ = φ₀ + ω₀ t + ε t ²/2,

где ω₀ – начальная угловая скорость, φ = 2π N.

Угловая скорость тела при равнопеременном вращении

ω = ω₀ + ε t.

11. Связь между линейными и угловыми величинами, характеризующими вращение материальной точки:

S = φR; v = wR; a _t = eR; a _n =

 

Колебания и волны

 

12. Кинематическое уравнение гармонических колебаний материальной точки

x = A sin(wt+j ₀),

где x – смещение; А – амплитуда колебаний; w - круговая или циклическая частота; j ₀ – начальная фаза.

13. Скорость материальной точки, совершающей гармонические колебания

v = A wcos(w t + j ₀) = v _msin(ω t + φ₀ + π/2).

14. Ускорение материальной точки, совершающей гармонические колебания

a = A w²sin(w t + j ₀) = а _msin(w t + j ₀ + π).

15. Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

А =

б) начальная фаза результирующего колебания

16. Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях (x = A ₁cos w t, y = A ₂cos(w t + j ₀)):

а) y = 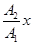(если разность фаз D j = 0);

б) y = (если разность фаз D j = ±p);

в) (если разность фаз D j = ±p/2).

17. Уравнение плоской бегущей волны

y = A cos w (t - ),

где y – смещение любой из точек среды с координатой х в момент t, v – скорость распространения колебаний в среде.

18. Связь разности фаз D j колебаний с расстоянием D х между точками среды, отсчитанным в направлении распространения колебаний

,

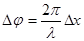где l - длина волны.

Динамика

 

1. Поступательное движение

 

19. Импульс материальной точки, движущейся поступательно со скоростью v

.

20. Второй закон Ньютона

,

,

где - сила, действующая на тело.

21. Силы, рассматриваемые в механике:

а) сила упругости

F = - k x,

где к - коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;

б) вес - сила, с которой тело действует на опору или подвес;

в) сила гравитационного притяжения

,

где m ₁ и m ₂ – массы взаимодействующих тел; r – расстояние между телами (тела – материальные точки или сферы). Силу можно выразить и через напряженность G гравитационного поля

F = mG;

г) сила тяжести

F = mg,

где g – ускорение свободного падения;

д) сила трения скольжения

F _тр = m N,

где m - коэффициент трения; N – сила нормальной реакции опоры.

22. Закон сохранения импульса

Для двух тел (i = 2)

,

где v ₁ и v ₂ – скорости тел в момент времени, принятый за начальный; u ₁ и u ₂ – скорости тех же тел в момент времени, принятый за конечный.

23. Кинетическая энергия тела, движущегося поступательно

24. Потенциальная энергия:

а) упруго деформированной пружины

,

где к – жесткость пружины; х – абсолютная деформация;

б) гравитационного взаимодействия

,

где g - гравитационная постоянная; m ₁ и m ₂ – массы взаимодействующих тел; r – расстояние между ними (тела – материальные точки или сферы);

в) тела, находящегося в однородном поле силы тяжести,

П = mgh,

где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R - радиус Земли).

25. Закон сохранения механической энергии

Е = Т + П = const,

если система консервативна, т.е. работа неконсервативных сил А ^н/к (F _Т, F _cопр) = 0.

26. Механическая работа

A = F s cosa,

или

А = DЕ = Е ₂ – Е ₁,

работа – как мера изменения энергии.

А ^{консервативных} = - ΔП, А ^н/к = Е _М2 – Е _М1.

 

2. Вращательное движение

 

27. Момент импульса тела, вращающегося относительно неподвижной оси

,

где w - угловая скорость тела.

28. Основное уравнение динамики вращательного движения относительно неподвижной оси

= I ,

где М – результирующий момент внешних сил, действующих на тело; e - угловое ускорение; I – момент инерции тела относительно оси вращения.

29. Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс:

а) стержня длины l относительно оси, перпендикулярной стержню,

;

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра);

I = mR ²;

в) диска радиусом R относительно оси, перпендикулярной плоскости диска,

.

30. Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси

для двух тел

I ₁w₁ + I ₂w₂ = I ₁^′w′₁ + I ^′w^′₂,

где I ₁, w_1, I _2, w₂ – моменты инерции и угловые скорости тел в момент времени, принятый за начальный; I ₁^′, w′₁, I, ^′w^′₂ – те же величины в момент времени, принятый за конечный.

31. Кинетическая энергия тела, вращающегося вокруг неподвижной оси

 

 

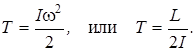
4.1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

 

№ 1. Зависимость угла поворота тела от времени дается уравнением j = А + Вt +Ct ² + Dt ³, где А = 1 рад, В = 0,1 рад/с, D = 0,01 рад/с². Найти: а) угловой путь, пройденный за 3 с от начала отсчета времени; б) среднюю угловую скорость; в) среднее угловое ускорение за 3 с от начала движения.

Р е ш е н и е.

Угловой путь, пройденный за 3 с, равен j = j ₂ - j ₁, где j ₂ - угловой путь, пройденный за 3 с (t ₂ = 3c); j ₁ - угловой путь к моменту времени t ₁ = 0 c.

а) из зависимости углового пути от времени j (t) (см. условие задачи) найдем j ₁ и j ₂:

j ₁ = А = 1 рад.

j ₂ = А + Вt ₂² + Dt ₂³ = 1 + 0,1×3 + 0,02×3² + 0,01×3³ = 1,75 рад.

j = j ₂ - j ₁ = 1,75 - 1 = 0,75 рад.

б) средняя угловая скорость за 3 с от начала вращения выражается формулой

в) среднее угловое ускорение за 3 с от начала вращения

,

где w ₂ - угловая скорость в момент времени t ₂ = 3 c; w ₁ - угловая скорость в момент времени t ₁ = 0 с.

Мгновенную угловую скорость найдем по определению

= B + 2 Ct + 3 Dt ².

Подставим числовые данные:

t ₂ = 3 с. w ₂ = 0,1 + 2× 0,2 ×3 + 3×0,01×3² = 0,49 рад/с.

t ₁ = 0 c. w ₁ = B = 0,1 рад/с.

Среднее угловое ускорение

< e > = рад/с².

№ 2. Тело вращается вокруг неподвижной оси по закону

j = 10 + 20 t - 2 t ².

Найти полное ускорение точки (величину и направление), находящейся на расстоянии 0,1 м от оси вращения, для момента времени t = 4 с.

Р е ш е н и е.

Каждая точка вращающегося тела описывает окружность. Полное ускорение точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального , направленного по касательной к траектории, и нормального , направленного к центру кривизны траектории:

(1)

Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:

а _t = e R,(2)

a _n = w ² R, (3)

где w - угловая скорость тела; e - его угловое ускорение; R - расстояние точки от оси вращения.

Подставляя формулы (2) и (3) в (1), находим

. (4)

Угловая скорость вращающегося тела равна первой производной от угла поворота по времени

В момент времени t = 4 с угловая скорость

w = (20 - 4×4)с^-1 = 4 рад/с.

Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени

Это выражение не содержит аргумента времени t, следовательно, угловое ускорение имеет постоянное значение, не зависящее от времени.

Подставив значения w и e в формулу (4), получим

№ 3. Из орудия вылетает снаряд со скоростью v ₀ = 1000 м/с под углом 30⁰ к горизонту (сопротивление воздуха не учитывать).

Определить: радиус кривизны траектории R в верхней точке полета; максимальную высоту подъема; время движения; расстояние S, на которое упадет снаряд по горизонтали.

Р е ш е н и е:

1. Принцип независимости: если тело участвует одновременно в нескольких движениях, то одно движение от другого не зависит.

2. Принцип суперпозиции: однородные величины, относящиеся к одному объекту, могут быть сложены.

Движение тела, брошенного под углом к горизонту, можно представить как сложное, состоящее из двух более простых: равномерного - в горизонтальном направлении и равнопеременного - в вертикальном. Траекторией движения будет парабола.

На чертеже обозначим оси 0x и 0y, траекторию движения, начальную скорость v ₀, угол бросания a, высоту поднятия h, дальность полета S, скорость в момент падения v и угол падения b. Разложим векторы и на горизонтальные и вертикальные составляющие:

v _0x = v ₀cos a,

v _0y = v ₀sina.

Запишем уравнения скорости и пути для обоих направлений. По горизонтали:

v _x = v _0x = v ₀cos a = const., (1)

S = v _x 2 t = (v ₀cos a) t, (2)

где t - время поднятия снаряда до верхней точки.

 

По вертикали:

v _y = v _0y - gt = v ₀sin a - gt. (3)

h = v ₀ t sinα - gt ²/2. (4)

Это движение равнозамедленное.

1. Радиус кривизны траектории находим из формулы нормального ускорения

Определим а _n. Полное ускорение в любой точке траектории

.

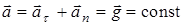В верхней точке траектории полная скорость определяется только составляющей скорости вдоль оси 0 Х, так как в этой точке v _y = 0: v _x = v _0x = const; Вследствие того, что составляющая скорости вдоль оси Ох – постоянная величина, касательное ускорение в верхней точке траектории a _t равно нулю. Следовательно,

;

a _n = g.

2. Высоту h найдем по уравнению (4), а время подъема по уравнению (3):

Подставив выражение времени t в формулу высоты h, получим

3. Путь S находим, применяя уравнение (3)

S = 2 v ₀cos a = 2 .

 

№ 4. Лифт опускается вниз и перед остановкой движется замедленно. Определить, с какой силой (вес тела) будет давить на пол лифта человек массой 60 кг, если ускорение лифта равно 4 м/с².

Р е ш е н и е.

1. Записать II закон Ньютона.

.

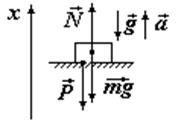
2. Сделать схематический чертеж, на котором указать силы, действующие на тело, ускорение тела и систему отсчета: - сила тяжести; - сила нормальной реакции опоры (пола кабины). По III закону Ньютона вес тела численно равен силе нормальной реакции , противоположно направленной и приложенной к опоре: = - .

3. Расписать второй закон Ньютона в векторной форме в соответствии с условием задачи

4. Записать это уравнение в скалярной форме, проектируя все векторы на ось (направление оси выбирается произвольно):

х: N - mg = ma.

Из этого уравнения выразить N

N = mg + ma.

Следовательно,

P = g(m + a).

Подставить числовые данные:

Р = 60(4 + 9,8) = 840 Н.

 

№ 5. Вагонетку массой 3 т поднимают по рельсам в гору, наклон которой 30⁰. Какую работу совершает сила тяги на пути в 50 м, если известно, что вагонетка двигалась с ускорением 0,2 м/с²? Коэффициент трения принять равным 0,1.

Р е ш е н и е.

Работа постоянной силы тяги F _т определяется по формуле

A = F _т S cos a.,

где α угол между силой и перемещением. Сила тяги направлена вдоль перемещения, поэтому угол a = 0 и cos a = 1.

1. .

2. Сделать чертеж.

3. Записать уравнение II закона Ньютона в векторной форме.

На тело действуют четыре силы:

Так как силы направлены под углом друг к другу, то систему отсчета составим из двух взаимно перпендикулярных осей x и y, развернув ее для удобства так, что одну ось направим вдоль наклонной плоскости, а другую - перпендикулярно ей.

4. Записать уравнение в проекциях на оси:

х: mg sin a - F _т + F _тр + 0 = - ma,

y: - mg cos a + 0 + 0 + N = 0,

F _тр = m N,

где m - коэффициент трения.

Решить систему трех уравнений относительно F _т

F _т = mg sin a + m mg cos a + ma = m (g sin a + m g cos a + a).

5. A = F _т S = m (g sin a + m g cos a + a) S.

Подставить числовые данные:

A = 3 10³ (0,2 + 10×0,5 + 0,1×10×0,87)50 = 900 кДж.

№ 6. Маховик, выполненный в виде диска радиусом 0,4 м и имеющий массу 100 кг, был раскручен до скорости вращения 480 об/мин и предоставлен самому себе. Под действием трения вала о подшипники маховик остановился через 1 мин 20 с. Определить момент силы трения вала о подшипники.

Р е ш е н и е.

Используем основное уравнение динамики вращательного движения

М D t = Iw ₂ - Iw ₁,

где М - тормозящий момент; D t - время действия тормозящего момента; I - момент инерции маховика; w ₂ - конечная угловая скорость; w ₁ - начальная угловая скорость.

Решая уравнение относительно М, получим:

Найдем числовые значения величин и подставим их в выражение для M.

Знак «минус» означает, что момент М - тормозящий.

№ 7. Железнодорожная платформа с установленным на ней орудием движется горизонтально со скоростью v ₀ = 1 м/с. Масса платформы вместе с орудием М = 2 ×10⁴ кг. Из орудия выпускается снаряд по ходу платформы со скоростью u ₁ = 800 м/с под углом a = 30⁰ к горизонту. Масса снаряда m = 20 кг. С какой скоростью u ₂будет двигаться платформа после выстрела?

Р е ш е н и е.

1. Записать закон сохранения импульса

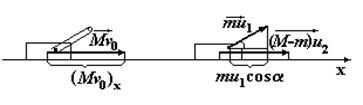
2. Сделать схематический чертеж с указанием импульсов тел системы, проекций и системы отсчета.

3. Написать уравнение в проекциях

(M - m) v ₀ + mv ₀ =

(M - m) u ₂ + mu ₁cos a,

4. Решить уравнение относительно u ₂

5. Подставить данные

 

№ 8. Платформа в виде диска радиусом R = 1,5 м и массой m ₁ = 150 кг вращается по инерции около вертикальной оси, делая n = 10 об/мин. В центре платформы стоит человек массой m ₂ = 60 кг. Какую линейную скорость относительно пола будет иметь человек, если он перейдет на край платформы?

Р е ш е н и е.

1. Записать закон сохранения момента импульса

или

I ₁w₁ + I ₂w₂ = I ₁^΄w₁^΄ + I ₂^΄w₂^΄.

2. Записать закон для задачи

(I ₁ + I ₂) w = (I ₁ + I ₂^΄) w^΄, (1)

 

где: I ₁ - момент инерции платформы; I ₂ - момент инерции человека, стоящего в центре платформы; w - угловая скорость платформы с человеком, стоящим в центре; I ₂^΄ - момент инерции человека, стоящего на краю платформы; w^΄ - угловая скорость платформы с человеком, стоящим на ее краю.

3. Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением:

v =w^΄ R. (2)

4. Угловую скорость w^΄ выразить из уравнения (1)

и подставить в уравнение (2)

. (3)

5. Момент инерции платформы - диска

момент инерции человека - материальной точки

I ₂ = 0; I ₂^’ = m ₂ R ².

Угловая скорость платформы w до перехода человека

w = 2 pn.

6. Подставить выражения I ₁, I ₂, I ₂^’ и w в формулу (3)

и упростить

7. Подставить числовые значения величин

 

№ 9. Трамвайный вагон массой 16 т движется по горизонтальному пути со скоростью 6 м/с. Какова должна быть тормозящая сила, чтобы остановить вагон на расстоянии 10 м?

Р е ш е н и е.

Большинство задач механики можно решать двумя способами: используя законы динамики или с помощью законов сохранения и превращения энергии. Предлагаемую задачу решим вторым способом.

1. Определить, какие силы действуют в системе. Так как в системе работают и консервативные силы (mg) и неконсервативные (F _тр), а движение горизонтальное, удобно применить теорему об изменении кинетической энергии

2. Сделать чертеж, на котором указать начальное и конечное положения тела, силы, скорость, ускорение и систему отсчета. Принять горизонтальный путь по рельсам за нулевой уровень потенциальной энергии.

3. Расписать уравнение

.

Кинетическая энергия в конечном состоянии mv ₂²/2 = 0, работы сил тяжести и нормальной реакции опоры в направлении оси х тоже равны нулю (А = F S cos a).

4. Записать уравнение в окончательном варианте

.

5. Определить силу торможения

Подставить данные

 

№ 10. Люстра весом 98 Н висит на цепи, которая выдерживает нагрузку 196 Н. На какой максимальный угол a можно отклонить люстру от положения равновесия, чтобы при последующих колебаниях цепь не оборвалась?

Р е ш е н и е.

1. Определить, какие силы действуют в системе (сила тяжести mg и сила натяжения нити F _н), и выбрать идею решения. Так как в задаче фиксируются два положения тела, а система консервативна (работа неконсервативных сил равна нулю), то решить задачу можно с использованием закона сохранения энергии.

Е _м = const, A ^нк = 0.

2. Сделать чертеж. За нулевой уровень потенциальной энергии удобно принять уровень положения равновесия (т. О). Отметить положения I и II системы, силы тяжести и натяжения, вектор нормального ускорения, скорость при прохождении положения равновесия, высоту h, на которую поднимается люстра, угол отклонения a.

3. Расписать закон сохранения энергии

Е _мI = E _мII; E _пI + 0 = 0 + E _кII; mgh = .

4. Так как этого уравнения недостаточно для нахождения неизвестного, применить II закон Ньютона для криволинейного движения и решить систему двух уравнений

1. mgh = ,

2. .

5. Записать второе уравнение в скалярной форме (через проекции на ось х):

х: , где R = l - длина нити.

Из первого уравнения выразить mv ² и подставить в х)

F _н - mg = .

6. Ввести неизвестное, обратившись к рисунку.

Из треугольника АВС: ВС = АВ cos a = l cos a.

h = l - l cos a = l (1- cos a)

Высотуподнятия h подставить в рабочее уравнение и найти a

F _н - mg = 2 mg (1- cos a),

cos a = ,

cos a = 0,5; a = 60⁰.

№ 11. Какую мощность N должен развить мотор самолета для обеспечения подъема самолета на высоту h = 1 км, если масса самолета m = 3000 кг, а время подъема t = 1 мин? Движение считать равноускоренным.

Р е ш е н и е.

1. Как и в предыдущих задачах, определить силы, действующие в системе, выбрать идею решения.

Так как система неконсервативна - на самолет действуют консервативная сила тяжести () и неконсервативная сила тяги (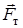), - а движение вертикальное, удобно выбрать закон превращения полной механической энергии.

Е _мII - Е _мI = A ^нк,

где Е _м = Е _к + Е _п.

2. Сделать чертеж

3. Расписать уравнение

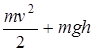() - 0 = A _Т,

где A _Т - работа силы тяги мотора, 0 - полная энергия в положении I.

4. Записать уравнение мощности по определению

и подставить в него выражение A _Т.

5. Выразить скорость v в конечном состоянии II, используя уравнения равноускоренного движения v ² - v ₀²= 2 ah и v = v ₀ + at, где v ₀ = 0.

h = v _ср t = (0 + v) t /2,

.

6. Подставить v в формулу мощности

7. Произвести вычисления

N _ср = 0,8 МВт.

 

№ 12. На краю диска, масса которого m и радиус R, стоит человек массой M. Диск совершает вращательное движение с частотой n об/с. Чему равна кинетическая энергия системы? Чему равна работа внешних сил, в результате действия которых частота вращения увеличивается вдвое?

Р е ш е н и е.

Записать формулу кинетической энергии вращающегося тела

(1)

где I - момент инерции системы; w - угловая скорость вращения системы.

Выразить момент инерции системы I и угловую скорость w. Момент инерции системы складывается из моментов инерции тел системы

I = I ₁ + I ₂,

где I ₁ = - момент инерции диска; I ₂ = - момент инерции человека. Угловая скорость w = 2p n. Подставить выражения I ₁ и I ₂ в формулу (1)

 

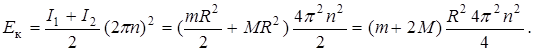
. (2)

Работу сил определить по теореме об изменении кинетической энергии

.

Используя уравнение (2) и условие n ₂ = 2 n ₁, записать

 

А = p ² 4 n ² R ²(m + 2M) - p ² n ² R ²(m + 2M) = 3 p ² n ² R ²(m + 2M).

№ 13. Материальная точка массой m = 0,01 кг совершает гармонические колебания по закону синуса с периодом Т = 2 с и начальной фазой j ₀, равной нулю. Полная энергия колеблющейся точки Е = 0,1 мДж.

Требуется: найти амплитуду А колебаний; написать закон данных колебаний x = f (t); найти наибольшее значение силы F _max, действующей на точку.

Р е ш е н и е.

1. Записать закон гармонических колебаний

x = A sin w t.

Так как закон не дает возможности определить амплитуду А, обратиться к условию задачи и воспользоваться полной энергией Е. Полная энергия колеблющейся точки Е равна, например, ее максимальной кинетической энергии Е _к,max.

Скорость v колеблющейся точки определить, взяв первую производную смещения х по времени

.

Учесть, что v _max = Aw (cos j =1) и подставить это выражение в уравнение энергии Е _к,max

Найти амплитуду колебаний

.

Выразить амплитуду через период Т, учитывая что .

.

Произвести вычисления

w = p с^-1

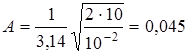м.

2. написать уравнение гармонических колебаний для данной точки:

х = 0,045sin pt.

3. записать второй закон Ньютона

| F _max| = ma.

Ускорение колеблющейся точки найти, взяв первую производную скорости по времени:

.

Максимальное ускорение (при sin w t = 1)

| a _мах| = A w².

Записать выражение силы

| F _max| = mA w².

Произвести вычисления

F _max = 0,01×0,045×3,14² Н = 4,44 10^-3 Н.

 

№ 14. Складываются два колебания одинакового направления, заданные уравнениями:

x ₁ = cosp (t + 1/6),

x ₂ = 2cosp (t + 1/2)

(длина в см, время в с).

Требуется: Определить амплитуды, периоды и начальные фазы складывающихся колебаний; Написать уравнение результирующего колебания.

Р е ш е н и е.

1. Записать уравнение гармонического колебания в общем виде:

x = A cos (). (1)

2. Привести заданные уравнения в соответствие с общим уравнением

х ₁ = A cos (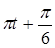), (2)

х ₂ = A cos (). (3)

3. Сравнить уравнения (2) и (3) с (1). Из сравнения: А ₁ = 1см; А ₂ = 2 см.

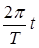= pt; 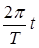= pt; Þ T ₁= 2c; T ₂ = 2c.

j ₀₁ = p / 6 рад = 30⁰; j ₀₂ = p / 2 рад = 90⁰.

Для написания уравнения результирующего колебания необходимо определить параметры результирующего колебания: T, А, j ₀.

1. Так как периоды колебаний одинаковы, период результирующего колебания будет тот же T = 2c.

2. Для определения амплитуды результирующего колебания А удобно воспользоваться векторной диаграммой. В системе координат х0y отложить под углами, соответствующими начальным фазам, векторы амплитуд и . На них, как на сторонах, построить параллелограмм, диагональ которого и будет амплитудой результирующего колебания. Ее величину определить, используя теорему косинусов.

А =

Подставить числовые значения

см.

Начальную фазу результирующего колебания определить по тангенсу угла j ₀.

,

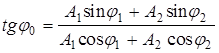откуда начальная фаза

.

Подставить данные

Таким образом параметры результирующего колебания найдены:

А = 2,6 см; Т = 2 с; j = 0,4 p рад.

Написать закон колебания

) см

или

x = 2,6 cos p (t + 0,4) см.

№ 15. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых имеют вид:

x = cos pt, (1)

y = 2cos , (2)

(амплитуда - в см, время - в с).

Определить траекторию точки и построить ее с соблюдением масштаба.

Р е ш е н и е.

Для определения траектории необходимо получить зависимость координат y = f(x). Для этого из уравнений (1) и (2) исключить время. Применив формулу косинуса половинного угла

можно записать

y=2 .

Так как cos p t = x (1), то

; у = .

или

y ² = 2 +2 x.

х	у =
-1
-0,75	± 0,1
-0,5	± 1
	± 1,41
0,5	± 1,73
	± 2

Полученное уравнение представляет собой уравнение параболы, ось которой лежит на оси Оx. Как показывают уравнения (1) и (2), амплитуда колебаний точки по оси Оx равна 1, а по оси Оy = 2. Следовательно, абсциссы всех точек траектории заключены в пределах от -1 до +1, а ординаты от -2 до +2.

Для построения траектории по уравнению (3) найти значения y, соответствующие ряду значений х, удовлетворяющих условию | x | £ 1.

Начертив координатные оси и выбрав масштаб, построить точки. Соединив их плавной кривой, получить траекторию точки. Она представляет собой часть параболы, заключенной внутри прямоугольника амплитуд АВСД. Из уравнений (1) и (2) находим периоды колебаний по горизонтальной и вертикальной осям Т _х и Т _у

, х = соs pt, y = 2cos .

t, с	x	y	положение точки
			положение А
	-1		вершина параболы
		- 2	положение D

Приравнивая аргументы, выразим Т _х

аналогично - Т _у = 4 с.

Следовательно, когда точка совершит одно полное колебание по оси Оx, она совершит только половину полного колебания по оси Оy. После этого она будет двигаться в обратном направлении.

 

№ 16. Физический маятник представляет собой стержень длиной l = 1 м и массой 3 m ₁ с прикрепленным к одному из его концов обручем диаметром D = l /2и массой m ₁. Горизонтальная ось маятника проходит через середину стержня перпендикулярно ему. Определить период T колебаний этого маятника.

Р е ш е н и е.

1. Записать формулу периода колебаний физического маятника

(1)

где I - момент инерции маятника относительно оси колебаний; m - его масса; d - расстояние от центра масс маятника (точка С) до оси колебаний (точка О).

2. Определить момент инерции системы. Момент инерции маятника равен сумме моментов инерции стержня I ₁ и обруча I ₂

I = I ₁ + I ₂. (2)

Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определить по формуле . В данном случае m = 3m и

.

Момент инерции обруча найти по теореме Штейнера

I ₂ = I ₀ + ma ²,

где I₂ = момент инерции обруча относительно произвольной оси; I ₀ - момент инерции, относительно оси, проходящей через центр масс обруча параллельно заданной оси; а - расстояние между указанными осями.

Найти момент инерции системы, подставив выражения I ₁ и I ₂ в формулу (2).

.

3. Найти расстояние d от оси колебаний до центра масс маятника

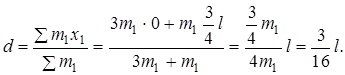
4. Определить период колебаний Т, подставив в формулу (1) момент инерции маятника I, расстояние d, массу системы (m = m ₁ +3 m ₁ = 4 m ₁).

Т = 2,17 с.

 

№ 17. Волна распространяется по прямой со скоростью v = 20 м/с. Две точки, находящиеся на этой прямой на расстоянии l ₁ = 12 м и l ₂ = 15 м от источника волн, колеблются по закону синуса с одинаковыми амплитудами А = 0,1 м и с разностью фаз Dj = 0,75 p. Найти: длину волны l; написать уравнение волны; найти смещение указанных точек в момент времени t = 1,2 с.

Р е ш е н и е.

1. Точки, находящиеся друг от друга на расстоянии, равном длине волны l, колеблются с разностью фаз, равной 2 p; точки, находящиеся друг от друга на любом расстоянии D l, колеблются с разностью фаз

Решить это уравнение относительно l

,

где D l - расстояние между точками, равное 3 м.

Подставить значения величин

= 8 м.

2. Записать уравнение плоской волны

s = A sin (w t – k x),

где к - волновое число 2p/ l,

или s = A sin w (t - ).

Найти циклическую частоту w,

решая систему относительно w, получаем

Написать уравнение волны

s = 0,1sin5 p (t - ).

3. Найти смещение s, подставляя в это уравнение значения t и l.

s ₁ = 0,1sin5p(1,2 - 12/20) = 0,1sin3 p = 0;

s ₂ = 0,1sin5p(1,2 - 15/20) = 0,1sin2,25 p = 1sin0,25p = 0,071 м.

 

4.2. ТРЕНИРОВОЧНЫЕ ЗАДАЧИ

 

1. Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением S = A + Bt ², где А = 6 м, В = -2 м/с². Найти момент времени t, когда нормальное ускорение точки а _n = 9 м/с², скорость v, тангенциальное ускорение а _t и полное ускорение точки а. (Ответ. 1,5 с; -6 м/c; -4 м/c²; 9,84 м/с²).

2. Две материальные точки движутся согласно уравнениям: x = A ₁ t +B ₁ t ² + C ₁ t ³ и x ₂ = A ₂ t + B ₂ t ² + C ₂ t ³, где А ₁ = 4 м/с; В ₁ = 8 м/с²; С ₁ = -16 м/с³; A ₂ = 2 м/c; B ₂ = -4 м/с²; С ₂ = 1 м/с³. В какой момент времени t ускорения этих точек будут одинаковыми? Найти скорости v ₁ и v ₂ точек в этот момент. (Ответ. 0,235 с; 5,1 м/с; 0,286 м/с).

3. Шар массой m ₁ = 10 кг сталкивается с шаром массой m ₂ = 4 кг. Скорость первого шара v ₁ = 4 м/c, второго - v ₂ = 12 м/с. Найти общую скорость u шаров после удара в двух случаях: 1) когда малый шар нагоняет большой шар, движущийся в том же направлении; 2) когда шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим. (Ответ. 6,28 м/с; -0, 573 м/с).

4. В лодке массой М = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью v = 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью u = 4 м/c (относительно лодки). Найти скорость лодки после прыжка человека: 1) вперед по движению лодка; 2) в сторону, противоположную движению лодки. (Ответ. 1м/с; 3 м/с).

5. Человек, стоящий в лодке, сделал шесть шагов вдоль нее и остановился. На сколько шагов передвинулась лодка, если масса лодки в два раза больше массы человека или в два раза меньше? (Ответ: 2 шага, 4 шага).

6. Из пружинного пистолета выстрелили пулькой, масса которой m = 5 г. Жесткость пружины к = 1,25 кН/м. Пружина была сжата на D l = 8 см. Определить скорость пульки при вылете из пистолета. (Ответ. 40 м/c).

7. Шар массой m ₁ = 200 г, движущийся со скоростью v ₁ = 10 м/с, ударяет неподвижный шар массой m ₂ = 800 г. Удар прямой, центральный, упругий. Определить скорости шаров после удара. (Ответ. -6 м/с; 4 м/с).

8. Шар, движущийся горизонтально, столкнулся с неподвижным шаром и передал ему 64% своей кинетической энергии. Шары упругие, удар прямой, центральный. Во сколько раз масса второго шара больше первого? (Ответ. в 4 раза).

9. Цилиндр, расположенный горизонтально, может вращаться около оси, совпадающей с осью цилиндра. Масса цилиндра m ₁ = 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m ₂ = 1 кг. С каким ускорением будет опускаться гиря? (Ответ. 1,4 м/с²; 8,4 Н).

10. Через блок, выполненный в виде колеса. Перекинута нить, к концам которой привязаны грузы m ₁= 100г и m ₂ = 300 г. Массу колеса считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения по обе стороны блока. (Ответ. 3,27 м/с²; 1,31 Н; 1,9 Н).

11. Двум одинаковым маховикам, находящимся в покое, сообщили одинаковую угловую скорость w = 63 рад/с и предоставили их самим себе. Под действием сил трения первый маховик остановился через одну минуту, а второй сделал до полной остановки N = 300 об. У какого маховика тормозящий момент больше и во сколько раз? (Ответ. У первого больше в 1,2 раза).

12. Шар скатывается с наклонной плоскости высотой h = 90 см. Какую линейную скорость будет иметь центр шара в тот момент, когда шар скатится с наклонной плоскости? (Ответ. 3,55 м/с).

13. На верхней поверхности горизонтального диска, который может вращаться вокруг вертикальной оси, проложены по окружности радиуса r = 50 см рельсы игрушечной железной дороги. Масса диска М = 10 кг, его радиус R = 60 см. На рельсы диска был поставлен заводной паровозик m = 1 кг и выпущен из рук. Он начал двигаться относительно рельсов со скоростью и = 0.8 м/с. С какой угловой скоростью будет вращаться диск? (Ответ. 0,195 рад/с).

14. Платформа в виде диска вращается по инерции около вертикальной оси с частотой n ₁ = 14 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до n ₂ = 25 об/мин. Масса человека m = 70 кг. Определить массу платформы М Момент инерции человека рассчитывать, как для материальной точки. (Ответ. 210 кг).

15. Искусственный спутник вращается вокруг Земли по круговой орбите на высоте h = 3200 км над Землей. Определить линейную скорость спутника. (Ответ. 6,45 км/с).

16. Точка совершает гармонические колебания. В некоторый момент времени смещение точки х = 5 см, скорость v = 20 см/с и ускорение а = -80 см/с². Найти циклическую частоту и период колебаний, фазу колебаний в рассматриваемый момент времени и амплитуду колебаний. (Ответ. 4 с ^-1; 1,57 с; p /4 рад; 7,07 см).

17. Точка совершает гармонические колебания, уравнение которых имеет вид: х = А sin w t, где А = 5 см, w = 2 с^-1. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки Е _п =10^-4 Дж, а возвращающая сила F = 5×10^-3 Н. Определить также фазу колебаний в этот момент времени. (Ответ. 2.04 с; 4,07 рад).

18. Два гармонических колебания, направленных по одной прямой, имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз складываемых колебаний. (Ответ. 120⁰ или 240⁰).

19. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: х = A ₁cos w ₁t и y = A ₂cos w ₂(t + t), где А ₁ = 4 см; А ₂ = 8 см; w ₁ = p с^-1; w ₂ = p с^-1; t = 1 с. Найти уравнение траектории и начертить ее с соблюдением масштаба. (Ответ. 2 х + у = 0.).

20. Поперечная волна распространяется вдоль упругого шнура со скоростью v = 15 м/с. Период колебаний точек шнура Т = 1,2 с. Определить разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях х ₁ = 20 м и х ₂ = 30 м. (Ответ. 200⁰).

ПРОВЕРОЧНЫЙ ТЕСТ

 

1. Тело движется по траектории, указанной на рисунке, так, что его нормальное ускоре­ние остается постоянным. В какой точке траектории скорость тела наибольшая?

Варианты ответа:

1) Q, 2) N, 3) M, 4) L, 5)K.

2. Мяч падает с высоты h. После отскока его скорость составляет 80% от скорости непосредственно перед ударом об пол. Высота, на которую поднимется мяч после удара, наиболее близка к:

Варианты ответа:

1) 0,647 h; 2) 0,947 h; 3) 0,807 h; 4) 0,757 h;5) 0,507 h.

3. Камень брошен под углом 60⁰ к горизонту. Как соотносятся между собой начальная кинетическая энергия Т ₁ камня с его кинетической энергией Т ₂ в верхней точке траектории?

Варианты ответа:

1) Т ₁ = 4 Т ₂; 2) Т ₁ = ¾ Т ₂; 3) Т ₁ = 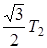; 4) Т<