В цепи (рисунок 30) с параметрами:
R1=15 Ом; R2=8 Ом; R3=20 Ом;
XL=20 Ом; XC1 =10 Ом; XC2 =15 Ом,
Рисунок 30
расчетным путем найдены токи:
Для составления баланса мощности найдем напряжение 
на зажимах источника тока (по второму закону Кирхгофа):
Тогда
Отсюда
Рист=8605,18 Вт; Qист=-2420,56 ВАр.
Найдём активную мощность потребителей:
Рпотр=13,7582 . 15+21,6952. 8+102. 20=8604,62 Вт.
Реактивная мощность потребителей:
Qпотр=13,7582. 20 - 21,6952. 10 - 102. 15= -2421,08 BАp.
Баланс мощности выполняется в пределах допустимой погрешности расчета (до 3%).
Метод эквивалентного генератора
Пусть какая-либо ветвь ab электрической цепи, в которой необходимо определить ток, содержит сопротивление Zab. Тогда по отношению к этой ветви вся остальная часть электрической цепи может быть заменена одним эквивалентным генератором с ЭДС 
и внутренним сопротивлением 
(рисунок 31).
Рисунок 31
Искомый ток равен
Параметры эквивалентного генератора , можно определить следующим образом. Величина равна напряжению на зажимах разомкнутой ветви (напряжение холостого хода):
Величину можно найти двумя способами:
1. Сопротивление равно входному сопротивлению цепи относительно зажимов а и b исходной схемы, из которой исключены все источники электрической энергии. При этом участок ветви, в котором был источник ЭДС, замыкается накоротко, а участок с источником тока размыкается (рисунок 32).
2. Замкнём участок ab накоротко (рисунок 33) и определим (опытным или расчётным путём) ток короткого замыкания 
. Тогда
Рисунок 32 Рисунок 33
Пример. Найдем ток 
в цепи (рисунок 29) методом эквивалентного генератора. Разомкнем ветвь с сопротивлением Z5 и определим величину 
(рисунок 34).
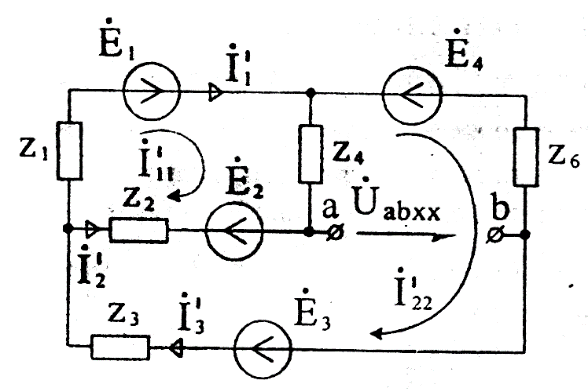
Рисунок 34
Предположим сначала, что токи в ветвях схемы нам известны. Составим уравнение по второму закону Кирхгофа так, чтобы в него входило искомое напряжение.
Тогда
Для расчетов токов 
можно воспользоваться известными способами расчета электрических цепей. Найдем их методом контурных токов:
Найдем величину Zr двумя способами.
1. Исключив из схемы источники ЭДС (рисунок 35), найдем величину входного сопротивления Zr относительно зажимов ab. Для этого заменим треугольник сопротивлений Z1, Z2, Z4 эквивалентной звездой Z7, Z8, Z9 (рисунок 36):
Тогда получим
Рисунок 35 Рисунок 36
2. Замкнем накоротко зажимы ab (схема рисунок 37) и найдем ток короткого замыкания методом контурных токов:
Рисунок 37
Тогда получим
окончательно искомый ток равен
Пример выполнения задания
В качестве примера рассчитаем электрическую схему (рисунок 38), для которой 
Z1=20+j30 Ом; Z2= -j45 Ом; Z3=10 Ом; Z4=50-j10 Ом; Z5=j80 Ом; Z6=30+j60 Ом; Z7=75-j25 Ом; Z8=20 Ом.
