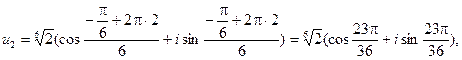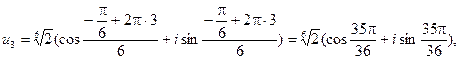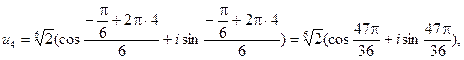Комплексное число z = a + bi можно задать с помощью радиус – вектора 
с координатами (a; b) (рис.4).
Рисунок 9 – Радиус – вектор комплексного числа
Длина вектора 
, изображающего комплексное число z, называется модулем этого числа и обозначается 
или r.
Для любого комплексного числа z его модуль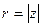 
определяется однозначно по формуле
Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное число, называется аргументом этого комплексного числа и обозначается
.
Очевидно, что у комплексного числа z имеется бесконечно много аргументов: если φ 0 − какой-либо аргумент числа z, то все остальные можно найти по формуле
φ = φ 0 + 2 πn, n 
Z.
Для комплексного числа z = 0 аргумент не определяется.
Из рисунка 9 видно, что
Тогда комплексное число можно представить в виде:
Такая форма записи называется тригонометрической формой записи комплексного числа.
Из последней системы находим:
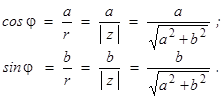
Таким образом, аргументом отличного от нуля комплексного числа z = а + bi является любое решение системы уравнений:
Среди всех аргументов комплексного числа z всегда есть один и только один, удовлетворяющий неравенствам:
0 ≤ φ < 2 π.
Это означает, что мы можем однозначно определить аргумент любого отличного от нуля комплексного числа.
Пример 4 Представить в тригонометрической форме комплексное число 1– i.
Решение: a = 1, b = -1.
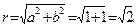
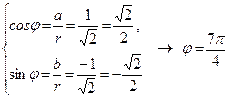
Действия над комплексными числами в тригонометрической форме
Умножение
Произведение комплексных чисел 
и 
находится по формуле
Таким образом, при умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Пример 5 Найти произведение комплексных чисел
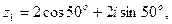
Решение: Тригонометрические формы этих чисел имеют вид:
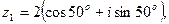
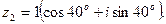
Тогда
Деление
Частное комплексных чисел и находится по формуле
,
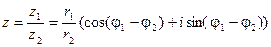Таким образом, при делении комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются.
Пример 6 Найти частное комплексных чисел
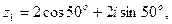
Решение: Тригонометрические формы этих чисел имеют вид:
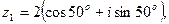
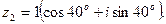
Тогда
Возведение в степень
Для возведения комплексного числа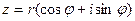 
в n -ю степень используется формула
,
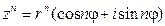где n – целое положительное число.
Это выражение называется формулой Муавра (Абрахам де Муавр (1667 – 1754) – английский математик)
Пример 7 Вычислите ( 1 + i) 100.
Запишем комплексное число 1 + i в тригонометрической форме.
a = 1, b = 1.
, 
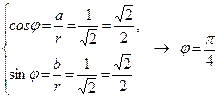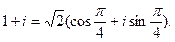
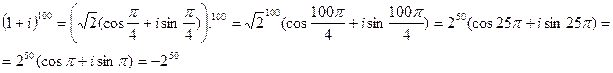4 Извлечение корня
Для извлечения корня n -й степени из комплексного числа 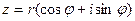используется формула
где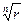 
- арифметический корень, 
.
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Пример 8 Вычислить u =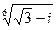 
.
Представим число z = 
в тригонометрической форме:
,
Поэтому согласно общей формуле Муавра
,
где k = 0, 1, 2, 3, 4, 5.
Таким образом, значения корней:
,
,
