План:
1 Системы m линейных алгебраических уравнений с n неизвестными
2 Методы решения систем линейных уравнений
Системы линейных уравнений
Система m линейных уравнений с n неизвестными имеет вид

где  – неизвестные системы
– неизвестные системы  .
.
 - коэффициент неизвестной
- коэффициент неизвестной  в
в  -ом уравнении.
-ом уравнении.
 - свободный член
- свободный член  -ого уравнения.
-ого уравнения.
В матричной форме система имеет вид:
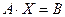 ,
,
где
 - матрица коэффициентов при неизвестных или
- матрица коэффициентов при неизвестных или
матрица системы.
 - матрица – столбец неизвестных.
- матрица – столбец неизвестных.
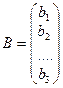 - матрица – столбец свободных членов.
- матрица – столбец свободных членов.
Если все свободные члены  , то система уравнений называется однородной; если хотя бы один
, то система уравнений называется однородной; если хотя бы один 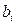 не равен нулю, то система называется неоднородной.
не равен нулю, то система называется неоднородной.
Пример 1
 - однородная система уравнений.
- однородная система уравнений.
 - неоднородная система уравнений.
- неоднородная система уравнений.
Решением системы называется совокупность n чисел (с1, с2, …, сn), при подстановке которых каждое уравнение системы обращается в верное равенство.
х1 = с1, х2 = с2, …, хn = сn
| Система уравнений | ||
| несовместная | совместная | |
| определенная | неопределенная | |
| не имеет решений |  решение решение
|  решения решения
|
Две системы уравнений называют равносильными, или эквивалентными, если они имеют одно и тоже множество решений.
Система равносильная данной получается может быть получена с помощью элементарных преобразований системы.
Элементарным преобразованием системы линейных уравнений называется:
1 Умножение коэффициентов при неизвестных и свободных членов на число не равное нулю.
2 Замена уравнений местами.
3 Прибавление к уравнению другого уравнения, предварительно умноженного на какое-либо число.
4 Приписывание к системе уравнения, которое является следствием.
Теорема (Кронекера–Капелли) Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы,т.е.

| Система m уравнений с n неизвестными | |||||

| |||||
 система несовместна
система несовместна
| 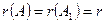 система совместна
система совместна
| ||||
 система определенная
система определенная

|  система неопределенная
система неопределенная

| ||||
Пример 2 Исследовать систему уравнений 
Решение: Определим ранги системы и расширенной матрицы.

Преобразуем матрицу А1, вычтя из элементов 2-ой строки и 3-ей строки элементы 1-ой строки, умноженной соответственно на 2 и на 3. Далее из элементов 3-ей строки вычтем элементы 2-ой строки.

Следовательно, система несовместна.
Пример 3 Исследовать систему уравнений 
Решение: Расширенная матрица системы имеет вид:

Вычтем из элементов 2-ой и 3-ей строки элементы 1-ой строки, умноженные соответственно на 2 и на 3, а затем к элементам 3-ей строки прибавим элементы 2-ой строки.

Следовательно, система несовместна. Т.к. ранг совместной системы менее числа неизвестных, то система неопределенная, т.е. имеет бесконечное множество решений.
Пример 4 Исследовать систему уравнений 
Решение: Здесь 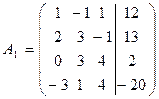
Вычтем из 2-ой строки 1-ую строку, умноженную на 2, прибавим к 4-ой строке 1-ую, умноженную на 3. Затем ко 2-ой строке прибавим 4-ую, умноженную на 2 и к 3-ей строке прибавим 4-ую.

Т.е.  , ранг системы равен числу неизвестных, следовательно, система совместная определенная, т.е. имеет одно решение.
, ранг системы равен числу неизвестных, следовательно, система совместная определенная, т.е. имеет одно решение.






