Средний участок уравнения Лэнгмюра вполне удовлетворительно описывается эмпирическим уравнением Фрейндлиха:
(IX.9)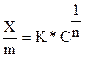 
, где:
x/m – количество адсорбированного вещества на единицу массы адсорбента;
с – равновесная концентрация вещества в растворе; K и 1/n – константы.
Физический смысл константы K становится ясным, если принять с =1, тогда K представляет собой количество адсорбированного вещества при равновесной концентрации, равной единице. Вторая константа 1/n обязательно является правильной дробью и характеризует степень приближения изотермы к прямой.
В отличие от уравнения Лэнгмюра (VII.21) уравнение Фрейндлиха(IX.9)не описывает всего процесса адсорбции: при малых концентрациях константа 1/n становится равной единицеи уравнение (IX.9) переходит в уравнение Генри; при больших концентрациях 1/n = 0 и количество адсорбированного вещества достигает постоянной величины Г∞. Тем не менее уравнение Фрейндлиха часто применяют для описания адсорбции слабых электролитов (типа уксусной кислоты) на твердых адсорбентах (таких, например, как активированный уголь).
При адсорбции из растворов членов одного и того же гомологического ряда, например жирных кислот, при переходе от уксусной кислоты (С2) к пентановой (С5) значения константы K будут возрастать от 0,1 до 0,34; тогда как значения второй константы 1/n будут уменьшаться от 0,41 до 0,23. С повышением температуры значения указанных констант меняются в обратном направлении: значения K – уменьшаются, а значения 1/n – увеличиваются.
Константы уравнения Фрейндлиха обычно находят графически по изотерме, построенной в логарифмических координатах. Если прологарифмировать уравнение (IX.9), то получим уравнение прямой, не проходящей через начало координат:
(IX.10) 
Взяв логарифмы экспериментально найденных значений x/m и сх иотложив их на осях координат, получают график, изображенный на рис. IX.11.
Отрезок, отсекаемый прямой на оси ординат, равен lgK, а тангенс угла наклона прямой к оси абсцисс(α) равен 1/n.
Количество вещества, адсорбированное одним граммом адсорбента x/m вычисляют по формуле (IX.11)
x/m = [(с0 – сх)*V*1000] / m, где:
с0 и сх – начальная и равновесная концентрации адсорбата, моль/л;
V – объем раствора, из которого проходит адсорбция, л; m– масса адсорбента, г.
1000 –переводной множитель для перевода величины x/m в ммоль/г.
Лабораторная работа №3
“Применение уравнения Фрейндлиха к адсорбции
органических кислот на твёрдых адсорбентах”.
В лабораторной работе исследуют процесс адсорбции из раствора уксусной кислоты на активированном угле. Перед началом работы тщательно промывают хромовой смесью, обычной водой, а затем дистиллированной водой 6 рабочих колб. В одну из них получают исходный раствор уксусной кислоты у преподавателя. Затем из исходного раствора готовят еще пять растворов путем разбавления каждого вдвое. Для этого в пять сухих колб наливают пипеткой по 50 мл дистиллированной воды. Затем отбирают пипеткой из колбы 50 мл исходного раствора, вносят их в первую из пяти приготовленных колб, хорошо взбалтывают, затем несколько раз набирают этот раствор в пипетку и выливают его обратно в ту же колбу, таким образом споласкивая пипетку приготовленным раствором. Отбирают из этой колбы 50 мл приготовленного раствора и переносят его во вторую колбу, снова хорошо перемешивают, так же как в предыдущем случае, споласкивают пипетку новым раствором и повторяют эту операцию до тех пор, пока не будут приготовлены все шесть растворов, включая исходный. Взвешивают шесть навесок активированного угля по 1 г каждая и вносят их по одной в каждую из шести колб с растворами. Встряхивают колбы с углем (порядка 2-3 минут) и оставляют в покое примерно на 50 -60 минут. Это свободное время используют для определения концентрации исходного раствора уксусной кислоты, который был получен у преподавателя. Делают это посредством титрования трех аликвот исходного раствора (по 10 мл каждая) раствором NaOH с известной концентрацией (этот раствор установлен в специальных емкостях непосредственно возле рабочего места).. По уравнению: 10мл*Nк-ты = VNaOH(мл)*NNaOH рассчитывают концентрацию в каждой пробе кислоты. Вычисляют среднюю концентрацию исходного раствора и проверяют её у преподавателя. По истечении 50-60 минут отфильтровывают приготовленные растворы, отбрасывая первые порции (около 10мл) фильтрата. Оставшийся раствор используют для титрования кислоты тем же раствором щёлочи, что и для исходного раствора (титруют по три порции каждого раствора). Полученные значения сх записывают в таблицу. Заметим, что до адсорбции нужно оттитровать только исходный раствор, а концентрации в остальных колбах после разведения просто рассчитывают посредством уменьшения в два раза концентрации кислоты в каждой последующей колбе. Полученные данные вносят в таблицы, как показано в образце оформления протокола работы, после чего строят график для определения констант в уравнении Фрейндлиха (рис.IX.11).
