3. 
4. Застосовують тільки для замкнених систем. Закон збереження імпульсу справедливий при взаємодії тіл будь-якої природи й не залежить від тривалості взаємодії.
Центр мас системи. Рух центра мас.
Імпульс системи може бути виражений через швидкість її центру мас.
Визначення. Центром мас (або центром інерції) системи матеріальних точок називається уявна точка С, положення якої характеризує розподіл маси цієї системи.
Іншими словами, центр мас є точка, у якій нібито зосереджена вся маса системи матеріальних точок.
Її радіус-вектор дорівнює (Рисунок 2.15) 
, де mi і ri - Відповідно маса і радіус-вектор і -ї матеріальної точки; n - кількість матеріальних точок у системі 
- маса системи.
| Рисунок 3.15 Радіус вектор центра мас системи матеріальних точок. |
Враховуючи, що 
, а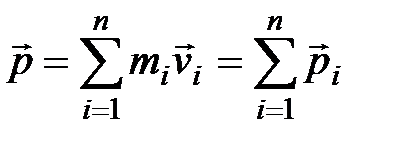 
, то можна написати: 
. Тобто імпульс системи дорівнює добутку маси системи на швидкість її центру мас.
Підставивши вираз 
у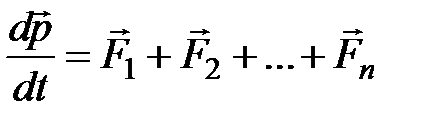 
, отримаємо: 
Тобто центр мас системи рухається як матеріальна точка, у якій зосереджена маса всієї системи й на яку діє сила, рівна геометричній сумі всіх зовнішніх сил, прикладених до системи. Вираз 
являє собою закон руху центру мас.
Згідно з формулою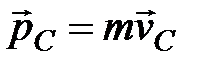 
із закону збереження імпульсу випливає, що центр мас замкнутої системи або рухається прямолінійно й рівномірно, або залишається нерухомим.
Запитання до лекції 2
1. У чому полягає перший закон Ньютона?
2. Що визначає маса тіла?
3. Яка система відліку називається інерціальною?
4. Які системи відліку називаються неінерціальними?
5. В чому полягає другий закон Ньютона?
6. Як розуміти поняття сили?
7. Дайте визначення імпульсу (кількості руху) матеріальної точки (тіла).
8. У чому полягає поняття імпульсу сили, що діє на матеріальну точку (тіло)?
9. У чому полягає третій закон Ньютона?
10. Яка система називається ізольованою (замкненою)?
11. У чому полягає закон збереження кількості руху (імпульсу)?
| Рисунок 3.1 До пояснення поняття механічної роботи. |
Лекція 3. Робота та енергія
3.1 Механічна робота. Визначення роботи змінної сили через лінійний інтеграл. Потужність. Зв’язок між роботою та потужністю.
Механічна робота А (ф.в.)
1. Механічна робота - це характеристика зміни стану системи тіл.
2. Визначення. Механічна робота - це фізична величина, яка чисельно дорівнює добутку сили F, що діє на тіло на переміщення s, яке здійснило тіло під дією сили й на косинус кута a між напрямками дії сили й переміщення тіла.
3. Механічна робота - це скалярна величина, але: (Рисунок 4.1) якщо 0°< a < 90°, то А > 0, (наприклад - тягнуть санчата); якщо a = 90°, то А = 0, (наприклад - робота сили тяжіння при горизонтальному переміщенні тіла); якщо 90° < a < 180°, то А < 0 наприклад - робота сили тертя.
4. А=Fscosa
5. [ А ]=Н·м=Дж (Джоуль). Існує несистемна одиниця вимірювання кВт·год. 1 кВт·год=3 600 000 Дж.
| Рисунок 3.2 До пояснення роботи змінної сили |
Визначення роботи змінної сили через лінійний інтеграл
Сила може змінюватися як по модулю, так і за напрямком, тому в загальному випадку формулою А = Fscosα користуватися не можна. Якщо, проте, розглянути елементарне переміщення dr, то силу F можна вважати постійною, а рух точки - прямолінійним. Елементарної роботою сили F на переміщенні dr називається скалярна величина
| Рисунок 3.3 Робота А визначається на графіку як площа тонованої фігури. |
dА = Fdr = Fcosαds = Fsds,
де α - кут між векторами F і dr; ds = | 
|- елементарний шлях; Fs - проекція вектора F на вектор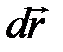 
(Рисунок 3.2).
Робота сили на ділянці траєкторії від точки 1 до точки 2 дорівнює алгебраїчній сумі елементарних робіт на окремих нескінченно малих ділянках шляху. Ця сума зводиться до інтеграла 
.
Для обчислення цього інтеграла треба знати залежність сили Fs від шляху s уздовж траєкторії 1 - 2. Представимо залежність графічно (Рисунок 3.3), на графіку шукана робота А визначається площею тонованої фігури.
Потужність N (Р) (ф.в.). Зв’язок між роботою та потужністю.
1. Потужність характеризує швидкість виконання роботи.
2. Визначення. Потужність - це фізична величина, яка чисельно дорівнює відношенню роботи A до часу t виконання цієї роботи.
3. Потужність - це скалярна величина.
4. 
, 
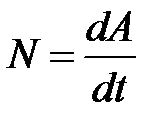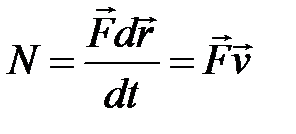, де F - сила, що діє на тіло, v - швидкість тіла.
5. [ N ]=Дж/с=Вт (Ват)
6. Визначення. Один Ват - це потужність, при якій сила виконує роботу в один Джоуль за одну секунду.
3.2 Консервативні та неконсервативні системи. Центральні сили. Механічна енергія системи тіл. Потенціальна енергія системи. Потенційна енергія стиснутої (чи розтягнутої) пружини. Потенційна енергія тіла в полі тяжіння Землі.
Консервативні та неконсервативні системи.
Визначення. Якщо робота, що здійснюється силами, залежить тільки від початкового й кінцевого положень тіла й не залежить від траєкторії його переміщення, то такі сили називають консервативними.
Системи, в яких діють тільки консервативні сили, називають консервативними. А поля, в яких діють ці сили - потенціальними.
Визначення. Якщо робота, що здійснюється силою, залежить від траєкторії переміщення тіла, то така сила називається дисипативною.
Системи, в яких діють дисипативні сили, називають неконсервативними.
Наприклад: сила тяжіння й сила пружності - консервативні сили. Сила тертя - дисипативна сила.
Тіла, перебуваючи в потенційному полі, мають потенційну енергією Wп.
Визначення. Потенційна енергія - це механічна енергія системи тіл, що визначається їх взаємним розташуванням і характером сил взаємодії між ними.
Центральні сили
Визначення. Сила F, яка діє на точку P, називається центральною з центром в точці O, якщо в увесь час руху вона діє вздовж лінії, яка з’єднує точки O і P.
Приклади центральних сил
Центральна сила ньютонівського тяжіння (величина сили F(r) пропорціональна 1 /r2)
Сила Кулона (величина сили F(r) пропорціональна 1/ r2)
Сила Гука (величина сили F(r) пропорціональна r)
Механічна енергія системи тіл
Енергія - це одна з фізичних величин, що характеризує стан тіла або системи тіл у даний момент часу. У механіці розглядають два види енергії - потенційну й кінетичну.
Потенціальна енергія системи
Тіла, перебуваючи в потенційному полі сил, мають потенційну енергією Wп. Потенційна енергія - механічна енергія системи тіл, яка визначається їх взаємним положенням і характером сил взаємодії між ними.
Визначення. Робота консервативних сил при елементарній (нескінченно малій) зміні конфігурації системи дорівнює зміні потенційної енергії, узятій зі знаком «-» (робота виконується за рахунок зменшення потенціальної енергії):
Робота dA виражається як скалярний добуток сили F переміщення dr, тому 
Звідки потенціальна енергія
де С - постійна інтегрування, тобто потенційна енергія визначається з точністю до деякої довільної постійної. Це, однак, не суттєво, оскільки в фізичні співвідношення входить або різниця потенціальних енергій у двох точках, або похідна функції П за координатами.
Тому потенційну енергію тіла, у якомусь певному положенні, умовно вважають рівною нулю (вибирають нульовий рівень відліку), а потенціальну енергію тіла в інших положеннях відлічують щодо нульового рівня.
Потенційна енергія стиснутої (чи розтягнутої) пружини дорівнює роботі, що здійснюється при її деформації: 
, де x – абсолютне значення деформації; k – жорсткість пружини.
Потенційна енергія тіла в полі тяжіння Землі дорівнює роботі при його підійманні: 
, де m - маса тіла, g – прискорення вільного падіння, а h – висота від нульового рівня енергії до центру мас тіла.
3.3 Кінетична енергія матеріальної точки. Теорема про зміну кінетичної енергії системи. Повна механічна енергія системи тіл. Закон збереження механічної енергії.
Кінетична енергія матеріальної точки Wк
1. Кінетична енергія матеріальної точки - це енергія рухомого тіла.
2. Визначення. Кінетична енергія матеріальної точки - це фізична величина, яка дорівнює півдобутку маси тіла (m) на квадрат його швидкості (v).
3. Кінетична енергія матеріальної точки - це скалярна величина.
4. 
Якщо рух точки задано в координатній формі, то кінетична енергія має вигляд: 
5. [ Wк ] = Дж
Теорема про кінетичну енергію
1. Установлює зв’язок між роботою, що виконують над тілом і кінетичною енергією тіла.
2. Визначення. Механічна робота, виконана над тілом, дорівнює зміні кінетичної енергії тіла.
3. 
; 
4. Застосовують тільки для замкнених систем.
Повна механічна енергія системи тіл.
Визначення. Повна механічна енергія системи - енергія механічного руху і взаємодії:
W = Wк + Wп,
Тобто дорівнює сумі кінетичної й потенціальної енергій.
Закон збереження повної механічної енергії
1. Закон збереження повної механічної енергії встановлює, що відбувається з повною механічною енергією при взаємодії тіл консервативними силами.
2. Визначення. У замкнутій системі повна механічна енергія тіла постійна величина.
3. W = Wк + Wп, =const
4. Межі застосування. Закон збереження повної механічної енергії справедливий тільки для замкнених систем.
Закон перетворення і збереження енергії
До цього було розглянуто перетворення механічної енергії в замкнених системах, у яких, відсутні сили тертя й сили непружних деформацій. Однак завжди в будь-якій системі тіл існують і тертя, і непружні деформації, які викликають зменшення повної механічної енергії системи.
Наприклад, при гальмуванні автомобіля його кінетична енергія зменшується, але він не набуває потенціальної енергії.
Пластилінова кулька при падінні на стіл прилипає до нього (не пружна взаємодія) Тобто її кінетична енергія в момент падіння не переходить у потенціальну. У наведених прикладах механічна енергія тіл зменшується.
Тертя одного тіла об інше, не пружна взаємодія кількох тіл приводить до нагрівання цих тіл, а це означає, що збільшується енергія руху молекул тіла або, як говорять, внутрішня енергія тіла. Тобто механічна енергія може перетворюватися у внутрішню енергію тіл. Численні досліди, проведені в кращих фізичних лабораторіях світу, показали, що перетворена частина механічної енергії в точності дорівнює збільшенню внутрішньої енергії, а повна енергія ізольованої системи й у цьому випадку залишається постійною. У цьому й полягає один із фундаментальних законів природи – закон перетворення і збереження енергії.
Визначення. Енергія ніколи не зникає й не виникає знову з нічого. Вона лише перетворюється з одного виду в інший або переходить від одного тіла чи системи тіл до іншого тіла чи до системи тіл, і при цьому виконується робота.
3.6 Пружні та не пружні зіткнення тіл
Удар (або зіткнення) - це зіткнення двох або більше тіл, при якому взаємодія триває дуже короткий час. При ударі сили взаємодії між тілами (ударні або миттєві сили) настільки великі, що всіма іншими силами можна знехтувати, систему таких тіл можна вважати замкненою. Для замкненої системи можна застосовувати закони збереження.
Сутність удару в тому, що кінетична енергія відносного руху тіл на короткий час перетворюється у енергію пружної деформації.
Під час удару має місце перерозподіл енергії між взаємодіючими тілами. Спостереження показують, що відносна швидкість тіл після удару не досягає свого колишнього значення. Це пояснюється тим, що немає ідеально пружних тіл й ідеально гладких поверхонь. Відношення швидкості тіл після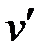 
і до удару 
називають коефіцієнтом відновлення ε.
Якщо для ε = 0, то такі тіла називаються абсолютно не пружними, якщо ε = 1 - абсолютно пружними. На практиці для всіх тіл 0 < ε <1 (наприклад, для сталевих куль ε ≈ 0,56, для куль із слонової кістки ε ≈ 0,89, для свинцю ε ≈ 0).
Тіла з великим ступенем відновлення можна розглядати як абсолютно пружні.
Запитання до лекції 3
1. Як визначається робота у випадку змінної сили?
2. Дайте визначення потужності та одиниці її виміру в системі CI.
3. Які сили називаються консервативними та неконсервативними? Наведіть приклади цих сил.
4. Дайте визначення кінетичній енергії.
5. Охарактеризуйте особливості потенціальної енергії.
6. Сформулюйте закон збереження та перетворення енергії.
7. Сформулюйте закон збереження механічної енергії.
8. Який зв'язок існує між консервативною силою, що діє на матеріальну точку, та її потенціальною енергією?
Лекція 4. Динаміка обертального руху твердого тіла навколо нерухомої осі
4.1 Обертання твердого тіла навколо нерухомої осі. Момент сили.
Обертання твердого тіла навколо нерухомої осі. Момент сили.
Для спрощення розв’язування задач використовують наближення – абсолютно тверде тіло.
Визначення. Абсолютно тверде тіло - це тіло, взаємне положення будь-яких точок якого не змінюється, в яких би процесах воно не брало участь. Іншими словами – це тіло, яке не можна деформувати.
В абсолютно твердому тілі силу можна переносити вдовж лінії дії сили.
Визначення. Лінія дії сили - це лінія, вздовж якої діє сила.
Визначення. Вісь обертання - це лінія, навколо якої може обертатися тіло.
| Рисунок 4.1 Напрямок моменту сили. |
Момент сили M
1. Момент сили - це характеристика обертального руху тіла.
2. Визначення. Моментом сили відносно якої-небудь точки називається векторний добуток радіуса-вектора, проведеного в точку прикладання сили на цю силу.
3. Вектор моменту сили напрямлений перпендикулярно до площини, проведеної через вектори 
і 
, і утворює з ними праву трійку векторів (при спостереженні з вершини вектора М (рисунок 4.1) видно, що обертання по найкоротшій відстані від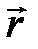 
до 
відбувається проти годинникової стрілки).
4. 
, де 
- радіус-вектор, проведений з точки О в точку прикладання сили.
| Рисунок 4.2 Знаходження проекції вектора сили на вісь z. |
або можна записати 
, де l плече сили - найкоротша відстань від точки О до лінії дії сили.
4. [ М ] = Н·м (Ньютон·метр).
*Момент сили відносно якої-небудь точки дорівнює нулю, якщо лінія дії сили проходить через цю точку.
*Проекція вектора сили на яку-небудь вісь, наприклад, вісь z, називається моментом сили відносно цієї осі. Щоб визначити момент сили відносно осі, спочатку проектують силу на площину, перпендикулярну осі (рисунок 4.2), а потім знаходять момент цієї проекції відносно точки перетину осі з перпендикулярної їй площиною.
*Якщо лінія дії сили паралельна осі або перетинає її, то момент сили відносно цієї осі дорівнює нулю.
4.2 Момент інерції тіла. Теорема Штейнера.
Момент інерції тіла Ј (йота)
1. Характеризує інертні властивості тіл при їх обертанні.
2. Визначення. Моментом інерції Јz тіла відносно осі z називається сума добутків мас точок цього тіла на квадрати відстаней від цих точок до осі.
3. Це скалярна величина.
4. 
, де mi - маса i -тої точки, ri - найкоротша відстань від i-тій точки до осі z.
Для суцільних тіл момент інерції визначається через інтеграл
, де r - відстань від елемента маси тіла dm до осі z.
5. [ Ј ] = кг·м2
*Моменти інерції однорідних тіл простої геометричної форми зазвичай розраховують за формулою, а складної - визначають експериментально. У таблиці 4.1 наведені моменти інерції деяких тіл.
Таблиця 4.1 - Моменти інерції однорідних тіл простої форми
| Тіло | Опис | Положення вісі a | Момент інерції Ja |
| Матеріальна точка маси m | На відстані r від точки. | 
|
| Порожнистий тонкостінний циліндр або кільце радіуса r і маси m. | вісь циліндра | 
|
| Суцільний циліндр або диск радіуса r і маси m | вісь циліндра | 
|
| Порожнистий товстостінний циліндр маси m із зовнішнім радіусом r2 і внутрішнім радіусом r1 | вісь циліндра | 
|
| Суцільний циліндр довжини l, радіуса r і маси m | Вісь перпендикулярна до циліндра і проходить через його центр мас | 
|
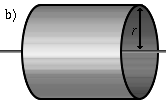
| Порожнистий тонкостінний циліндр (кільце) довжини l, радіуса r і маси m | Вісь перпендикулярна до циліндра і проходить через його центр мас |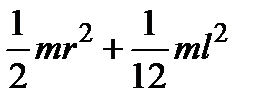 
|
| Прямий тонкий стрижень довжини l і маси m | Вісь перпендикулярна до циліндра і проходить через його центр мас | 
|
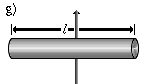
| Прямий тонкий стрижень довжини l і маси m | Вісь перпендикулярна до стрижня і проходить через його кінець |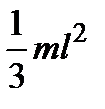 
|
| Тонкостінна сфера радіуса r і маси m | Вісь проходить через центр сфери | 
|
| Кулю радіуса r і маси m | Вісь проходить через центр кулі |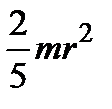 
|
| Рисунок 4.3 До пояснення теореми Штейнера |
Теорема Штейнера
1. Дозволяє розрахувати момент інерції тіла щодо довільної осі.
2. Визначення. Якщо для будь-якого тіла відомий його момент інерції Јkc щодо осі xc, що проходить через центр мас С тіла (рисунок 4.3), то момент інерції цього тіла відносно осі x1, паралельної xc, дорівнює.
3. 
де m - маса тіла, a - найменша відстань між осями x1 і xc.
4. Застосовують для обертання абсолютно твердого тіла.
4.3 Основний закон динаміки обертального руху. Умови рівноваги тіл
Основний закон динаміки обертального руху
1. Установлює зв'язок між моментом сил прикладених до тіла й кутовим прискоренням.
2. Визначення. Для тіла, що обертається навколо осі, сума моментів сил діючих на тіло дорівнює добутку моменту інерції на кутове прискорення тіла.
3. 
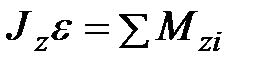де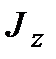 
- момент інерції тіла відносно осі обертання z, 
- кутове прискорення тіла, 
- сума моментів сил, прикладених до тіла, і розрахованих щодо осі обертання.
4. Застосовують тільки для абсолютно твердого тіла.
Умови рівноваги тіл
З 2-го закону Ньютона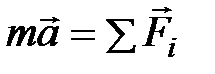 
й основного рівняння динаміки обертального руху 
витікають умови рівноваги для тіл, що знаходяться у спокої:
1) сума діючих на тіло сил повинна бути рівною нулю,
,
2) сума моментів сил щодо будь-якої точки тіла повинна дорівнювати нулю.
.
4.4 Момент імпульсу тіла, що здійснює обертання. Закон збереження моменту імпульсу
Момент імпульсу матеріальної точки, що здійснює обертання L
1. Характеризує кількість обертального руху.
2. Визначення. Моментом імпульсу 
матеріальної точки масою m, що рухається зі швидкістю 
, відносно довільної точки відліку O, називають векторний добуток радіус-вектора матеріальної точки на її імпульс.
| Рисунок 4.4 До пояснення моменту імпульсу. |
3. Це псевдовекторна величина, напрямок якої визначають за правилом правого гвинта.
4. 
, де 
- радіус-вектор матеріальної точки (Рисунок 4.4),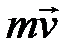 
- її імпульс.
Величина моменту імпульсу матеріальної точки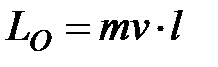 
, де l - найкоротша відстань від лінії вектора 
до точки О.
