ВСТУП
Світ навколо нас являє собою матерію. Невід’ємною властивістю матерії та формою її існування є рух. Рух у широкому розумінні слова - це різні зміни матерії - від простого переміщення до складних процесів мислення.
Фізика - наука про найбільш прості і разом з тим найбільш загальні форми руху матерії та їх взаємні перетворення. Форми руху матерії, що вивчаються фізикою (механічна, теплова та ін.), присутні в усіх вищих та більш складних формах руху матерії (хімічних, біологічних та ін.). Тому вони є у той же час найбільш загальними формами руху матерії. Вищі та більш складні форми руху матерії - предмет вивчення інших наук (хімії, біології та ін.).
Фізика тісно пов’язана з природничими науками (астрономією, геологією, хімією, біологією та ін.). В результаті була створена ціла низка нових суміжних дисциплін, таких як астрофізика, біофізика тощо.
Фізика тісно пов’язана і з технікою, причому цей зв’язок має двосторонній характер. Фізика виросла з потреб техніки (розвиток механіки у древніх греків, наприклад, був ініційований потребами будівельної та військової техніки того часу), і техніка, в свою чергу, визначає напрямок фізичних досліджень (наприклад, у свій час завдання створення найбільш економічних теплових двигунів викликала бурхливий розвиток термодинаміки). З іншого боку, від розвитку фізики залежить технічний рівень виробництва. Фізика - база для створення нових галузей техніки (електронна техніка, ядерна та ін.).
Важко переоцінити роль фізики при дослідженні якості та властивостей різноманітних товарів. Підвищення якості суттєво залежить від створення нових, більш точних та досконалих методів контролю сировини, технологічних процесів та готової продукції.
У харчових галузях промисловості більша частка вимірювальної інформації надходить за допомогою лабораторних засобів інформації. Створення нових засобів вимірювнь приводить до того, що все ширше впроваджуються такі прогресивні види вимірювальної техніки, як хроматографи, ЯМР – аналізатори та ін. Суттєві якісні зміни відбуваються з традиційними засобами вимірювань, що пов’язано з бурхливим розвитком обчислювальної техніки.
У посібнику матеріал із фізики систематизовано за планами, що допоможе студентам створити стислий конспект. Такий конспект дозволить їм краще орієнтуватися в основних положеннях фізики, систематизувати і правильно будувати свою відповідь. Нижче приведено плани викладання матеріалу, за якими побудовані відповіді до теоретичного матеріалу.
Плани подачі матеріалу
| Сила 1. Визначення сили. 2. Напрямок дії сили. 3. Модульне значення сили. 4.Пояснення природи сили за видом взаємодії. Прилад 1. Призначення приладу. 2. Схематичне позначення приладу (якщо воно існує). 3. Будова приладу. 4. Принцип дії приладу. Фізична величина (ф.в) 1. Яке явище або властивість тіл характеризує дана фізична величина 2. Визначення фізичної величини. 3. Яка це фізична величина – скалярна, чи векторна. 4. Формула розрахунку даної фізичної величини. 5. Одиниці вимірювання фізичної величини. 6. Визначення одиниці вимірювання фізичної величини (якщо воно існує). 7. Способи вимірювання фізичної величини. Явище 1. Знайомство з зовнішніми признаками явища і його використанням. 2. Визначення явища. | Дослід 1. Мета досліду. 2. Схема досліду. 3. Хід досліду. 4. Результат досліду. Закон (формула, рівняння) 1. Між якими явищами або величинами закон встановлює зв’язок. 2. Визначення закону. 3. Математичний запис закону. 4. Межі застосування закону. 3. Умови протікання явища. 4. Математичний опис явища. 5. Пояснення явища на основі вивчених законів. Поле 1. Поле як особивий вид матерії 2. Що породжує поле? 3. На що діє поле? 4. Основні характеристики поля. 5. Принцип суперпозиції для поля. 6. Потенціальність поля. 7. Взаємодія поля з речовиною. 8. Швидкість розповсюдження поля у просторі. 9. Як залежить густина поля від відстані до його джерела? 10. Способи графічного зображення поля. |
Лекція 1 Кінематика матеріальної точки
1.1 Механічний рух. Система відліку. Радіус-вектор. Рівняння руху у векторній та координатній формах. Основні кінематичні характеристики руху: траєкторія, переміщення, шлях, швидкість, прискорення. Зв’язок між ними.
Кінематика
Визначення. Механіка - це розділ фізики, предметом вивчення якого є рух макроскопічних тіл, що здійснюється з швидкостями набагато меншими за швидкість поширення світла.
Визначення. Механічний рух - це зміна положення тіла відносно інших тіл з часом.
Визначення. Основне завдання механіки - знаходження положення тіла в будь-який момент часу.
Визначення. Кінематика точки - це розділ кінематики, що вивчає математичний опис руху матеріальних точок.
Визначення. Основним завданням кінематики є опис руху за допомогою математичного апарату без з'ясування причин, що викликають цей рух.
Рух будь-якого об'єкта в кінематиці вивчають по відношенню до деякої системи відліку.
| Рисунок. 1.1 Поступальний і не поступальний рухи тіла |
Визначення. Система відліку - це тіло відліку, система координат, пов'язана з ним, і прилад для вимірювання часу.
Положення точки визначається набором узагальнених координат - впорядкованим набором числових величин, що повністю описують положення тіла у просторі. У найпростішому випадку це координати точки (радіус-вектора) у вибраній системі координат.
Основні кінематичні поняття
Визначення. Матеріальна точка (М.Т.) - це тіло, розмірами якого можна знехтувати за даних умов. Таких умов дві:
| Рисунок 1.2 Векторний спосібзавдання положення м.т. в просторі. |
б) Поступальний рух - це рух, при якому всі точки тіла рухаються однаково. Наприклад (рис.1.1):
Способи завдання положення М.Т. в просторі
Координатний спосіб (Рис. 1.2). Найбільш часто з цією метою використовують прямокутну систему координат. Положення точки A в тривимірній системі XYZ задається вказівкою значень трьох її проекцій x, y, z на осі координат X, Y, Z.
Векторний спосіб (Рис. 1.2). Положення матеріальної точки А в системі XYZ можна задати також за допомогою радіуса-вектора r, що з'єднує початок відліку - точку О з точкою М. Величина вектора r визначається його значенням (модулем) 
і напрямом, заданим кутами ф, δ.
| Рисунок 1.3 Графік переміщення при рівноприскореному русі тіла |
Проекції вектора r на осі координат розраховуються, виходячи з таких рівностей:
z = |r|·cos( δ );
y = |r|·sin( δ )·sin(ф);
x = |r|·sin( δ )·cos(ф).
Природний, або траєкторний, спосіб використовують тоді, коли відома траєкторія точки по відношенню до вибраної системи відліку. Положення точки визначається відстанню s = O1 M від вибраного на траєкторії початку відліку O1, виміряним уподовж дуги траєкторії й узятим з відповідним знаком (рис. 3), а закон руху дається рівнянням s = f (t), що виражає залежність s від часу t.
При природному способі будують графік, на якому у вибраному масштабі відкладені уздовж осі t час, а уздовж осі s - відстань (рисунок 1.3), або таблицею, де в одному стовпці даються значення t, а в іншому відповідні йому значення s.
1.2 Основні кінематичні характеристики руху: траєкторія, переміщення, шлях, швидкість, прискорення. Зв’язок між ними.
Визначення. Траєкторія - це уявна лінія, яку описує кінець радіус-вектора в процесі руху.
Іншими словами, траєкторія - це лінія, уздовж якої рухається М.Т.
Довжину ділянки траєкторії між початковим і кінцевим моментами часу часто називають пройденим шляхом і позначають буквою S. При такому описі руху S виступає в якості узагальненої координати, а закони руху в цьому випадку записується у вигляді
S = S(t) і аналогічні відповідним законам для координат.
| Рисунок 1.4 До пояснення основних кінематичних величин |
, 
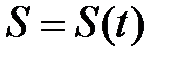
Де: 
- модуль початкової швидкості, а 
- тангенціальне прискорення.
Опис руху за допомогою поняття траєкторії - це один з ключових моментів класичної механіки. У квантовій механіці руху не має траєкторії, і поняття траєкторії взагалі втрачає сенс.
Основні кінематичні величини (рис. 1.4): радіус-вектори й вектор переміщення (чорні стрілки); вектори середньої й миттєвих швидкостей (зелені стрілки); траєкторія (червона лінія).
Переміщення
Визначення. Переміщення - векторна фізична величина, що дорівнює різниці радіус-векторів у кінцевий і початковий моменти часу:
.
Іншими словами, переміщення - це прирощення радіус-вектора за обраний проміжок часу.
Середня швидкість
Визначення. Середня швидкість - векторна фізична величина яка дорівнює відношенню вектора переміщення до проміжку часу, за який відбувається це переміщення:
.
Миттєва швидкість
1. Характеризує швидкість переміщення матеріальної точки. Миттєву швидкість можна визначити як межу середньої швидкості при прямуванні до нуля проміжку часу, на якому вона обчислюється:
.
2. Визначення. Миттєва швидкість - це векторна фізична величина, що дорівнює першій похідній від радіус-вектора за часом:
3. Миттєва швидкість завжди напрямлена по дотичній до траєкторії.
4. 
.
5. Одиниця вимірювання швидкості в системі СІ - [ v ] = м/с.
Не системна одиниця - км/год. 1 км/год = 1000м/3600с = 1/3,6 м/с.
18 км/год = 5 м/с, 54 км/год = 15 м/с, 90 км/год = 25 м/с,
36 км/год = 10 м/с; 72 км/год = 20 м/с, 108 км/год = 30 м/с
6. Прилад для вимірювання - спідометр.
Миттєве прискорення
1. Характеризує швидкість зміни швидкості.
2. Визначення. Миттєве прискорення - це векторна фізична величина, що дорівнює другій похідній від радіус-вектора за часом і, відповідно, першій похідній від миттєвої швидкості за часом.
3. У випадку руху в площині вектор прискорення можна розкласти по супутньому базису: на вектор нормального й тангенціального прискорення.
4. 
.
5. Одиниця прискорення в системі СІ - [ 
] = м/с2
6. Прилад для вимірювання - акселерометр.
1.3 Поступальний рух тіла. Рівномірний та рівноприскорений рухи.
Рівномірний прямолінійний рух
Рисунок 1.5
До пояснення рівномірного прямолінійного руху тіла.
1. Визначення. Рівномірний прямолінійний рух - це такий рух, при якому тіло за рівні проміжки часу здійснює однакові переміщення.
2. Вивчити рівномірний прямолінійний рух означає записати для нього рівняння координати.
3. x=x0+vxt. Де (Рис. 1.5) x0 –початкова координата; x - кінцева координата; v - швидкість тіла; t – час руху тіла.
Рівноприскорений прямолінійний рух
1. Рівноприскорений прямолінійний рух - це такий рух при якому тіло за рівні проміжки часу змінює свою швидкість на однакову величину.
2. Вивчити рух означає записати для нього рівняння координати.
| Рисунок 1.6 До пояснення рівноприскореного руху тіла. |
3. 
4. (Рис. 1.6) x - кінцева координата тіла; x0 – початкова координата тіла; v0 – початкова миттєва швидкість; а - прискорення, t - час руху тіла.
Обернена задача динаміки
Розв’язання оберненої задачі – визначення швидкості й закону руху точки по заданому прискоренню – проводиться шляхом інтегрування проекцій прискорення за часом, причому задача буде мати однозначний розв’язок, якщо, крім прискорення, задані ще й початкові умови – проекції швидкості й координати точки в початковий момент часу.
Закон рівноприскореного руху
Закон рівноприскореного руху виходить у результаті розв’язання простого диференціального рівняння виду: 
Загальний розв’язок цього рівняння дається формулою:
, де С1 і С2 - довільні константи, відповідні початковій координаті й початковій швидкості.
Рух із постійним прискоренням 
називають рівноприскореним. Рух з постійним прискоренням здійснюється за законом:
; 
.
При цьому рівняння руху у координатній формі мають аналогічний вигляд:
; 
.
| Рисунок 1.7 Переміщення при рівнозмінному русі |
У цьому випадку часто говорять про рівноприскорений рух, якщо знаки аx і vx(t) збігаються, і про рівносповільнений, якщо аx і vx(t) мають протилежні знаки. При цьому знак кожної з величин залежить від початкового вибору системи відліку.
Формули переміщення при рівнозмінному русі
Переміщення при рівнозмінному русі можна розрахувати за формулами:
; 
; r1: r2:r3…= 1:3:5… (Рисунок 1.7) де r1, r2,r3 – переміщення тіла за 1, другу і третю секунду руху.
| Рисунок 1.8 Вільний рух тіла в полі тяжіння Землі |
1.4 Вільний рух тіла в полі тяжіння Землі.
1. Визначення. Вільний рух тіла в полі тяжіння Землі (вільне падіння тіл) - це рух тіл внаслідок притягання їх Землею при відсутності сил опору.
2. Вивчити вільне падіння означає записати для нього рівняння координати.
3. (Рис. 1.8) 
; 
4. y0 початкова координата; y - кінцева координата; vo - початкова швидкість; v-кінцева швидкість; g - прискорення вільного падіння; t - час.
Прискорення вільного падіння g (ф.в.)
1. Прискорення вільного падіння - це силова характеристика гравітаційного поля (якщо її помножити на масу, то отримаємо силу F=mg).
2. Визначення. Прискорення вільного падіння - це прискорення, з яким рухаються тіла, внаслідок притягання їх Землею (планетою) при відсутності сили опору.
3. Прискорення вільного падіння - це векторна величина напрямлена до центру Землі (планети).
4. 
, де G - постійна всесвітнього тяжіння G = 6,67·10-11 Н·м2/кг2, М - маса Землі. М = 5,98·1024 кг; R - радіус Землі. R = 6,4·106 м. h - висота над поверхнею землі.
*Якщо h < R, то g = 9,8 м/с2
Переміщення при вільному падінні тіл 
Переміщення при вільному падінні тіл позначають 
і обчислюють за формулами 
і 
Звернути увагу!!!
* g для всіх тіл однакове.
*Якщо t невідоме, то 
*Якщо тіло кинули вгору на висоті ymax v= 0.
| Рисунок 1.10 Рух тіла кинутого під кутом до горизонту поблизу поверхні Землі. |
* |v| =|v0|
* tпідйому = tпадіння
Рух тіла під дією сили тяжіння
Рух тіла під дією сили тяжіння – це рух тіл кинутих під кутом до горизонту поблизу поверхні Землі при відсутності сил опору середовища.
Траєкторією такого руху є парабола (Рис.1.10)
Вивчити рух тіла під дією сили тяжіння означає записати для нього рівняння координат.
Рух тіла під дією сили тяжіння описують за допомогою двох координат 0x і 0y. Уздовж осі 0х на тіло кинуте під кутом до горизонту ніякі сили не діють, тому складова швидкості vx з часом не змінюється. vx=v0x, а координата змінюється за законом x=x0+v0xt.
Уздовж осі 0y на тіло, кинуте під кутом до горизонту діє сила тяжіння, тому складова швидкості vy з часом змінюється за законом vy =v0y-gt,а координата змінюється за законом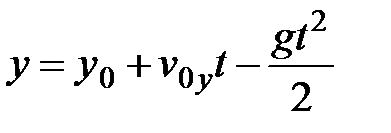 
, де g - прискорення вільного падіння.
У будь-якій точці траєкторії кут b, під яким тіло рухається по відношенню до горизонту, можна розрахувати за формулою 
.
Модуль швидкості тіла, кинутого під кутом до горизонту в будь-якій точці траєкторії розраховують за формулою 
.
На максимальній висоті підйому Н проекція швидкості тіла, кинутого під кутом до горизонту vy=0.
Для тіла, кинутого під кутом до горизонту час підйому дорівнює часу падіння tпадіння = tпідйому
Іноді для відшукання y можна користуватися формулою 
.
1.5 Криволінійний рух. Нормальна та тангенціальна складові повного прискорення при криволінійному русі матеріальної точки. Кінематика руху матеріальної точки по колу. Кут повороту, кутова швидкість та кутове прискорення. Зв’язок між лінійними та кутовими характеристиками руху.
Криволінійний рух
Визначення. Криволінійним рухом називають рух тіла по траєкторії, що не являє собою пряму лінію.
| Рисунок 1.11 Нормальна та тангенціальна складові прискорення матеріальної точки. |
Нормальна та тангенціальна складові повного прискорення при криволінійному русі матеріальної точки.
У випадку руху в площині вектор прискорення можна розкласти по супутньому базису: на вектор нормального й тангенціального прискорення (Рис. 1.11):
.
Де 
- одиничний вектор нормалі [1], 
- одиничний вектор дотичної. Величина 
називається нормальним прискоренням. Величина 
називається тангенціальним прискоренням
Нормальне прискорення 
1. У випадку руху по колу нормальне прискорення називається доцентровим.
2. Визначення. Нормальне прискорення - це прискорення, яке виникає в результаті зміни швидкості за напрямком.
3. Нормальне прискорення - це векторна величина, яка завжди спрямована по нормалі до дотичної.
4. Нормальне прискорення виражається через миттєву швидкість і радіус кривизни траєкторії: 
.
5. [ an ] = м/с2
*Як видно з попередньої формули, при русі по колу з постійною швидкістю нормальне прискорення постійне по модулю й направлено до центру кола.
Тангенціальне прискорення
1.Тангенціальне прискорення - це компонента прискорення, спрямована по дотичній до траєкторії руху. Характеризує зміну модуля швидкості з часом.
2. Визначення. Тангенціальне прискорення дорівнює добутку одиничного вектора, напрямленого по швидкості руху, на похідну модуля швидкості за часом.
3. Це векторна величина, спрямована в ту ж сторону, що й вектор швидкості при прискореному русі (позитивна похідна) і в протилежну - при уповільненому (негативна похідна).
4. 
.
5. [ aτ ] = м/с2
Рівноприскорений обертальний рух
Обертальний рух тіла залежно від часу t характеризують кутові величини: φ (кутове переміщення або кут повороту в радіанах), ω (кутова швидкість у рад/с) і ε (кутове прискорення в рад/с2).
Закон обертального руху тіла виражається рівнянням φ = f(t).
Кутова швидкість w (ф.в.)
1. Кутова швидкість - це характеристика обертального руху тіла, яка показує на який кут повертається тіло за одиницю часу.
2. Визначення. Кутова швидкість - це фізична величина, яка дорівнює відношенню зміни кутового переміщення, до часу цієї зміни.
3. Кутова швидкість - це псевдовекторна величина.
4. 
5. [ ω ] = рад/с
6. Прилад для вимірювання - тахометр.
| Рис. 1.12 Кутові та лінійні величини обертового руху. |
Кутове прискорення ε (епсилон)
1. Кутове прискорення - це величина, що характеризує швидкість зміни кутової швидкості.
2. Визначення. Кутове прискорення - це перша похідна кутової швидкості за часом.
3. Кутове прискорення - це псевдовекторна фізична величина.
4. 
.
5. [ ε ] = рад/с2
Залежність між кутовими та лінійними величинами обертального руху
При обертальному русі тіла всі його точки рухаються по колах, центри яких розташовані на одній нерухомій прямій (вісь обертальнго тіла). Установимо залежність між кутовими величинами φ, ω і ε, що характеризують обертальний рух тіла, і лінійними величинами s, v, aτ і an, що характеризують рух різних точок цього тіла (Рис. 1.12).
Якщо R - відстань від геометричної осі обертового тіла до деякої точки А (на рисунку 1.12 R = OA), то залежність між φ - кутом повороту тіла й s - відстанню, пройденою точкою тіла за той же час, виражається так: s = φR.
Залежність між кутовою швидкістю тіла і швидкістю точки в кожен даний момент виражається рівністю v = ωR.
Тангенціальне прискорення точки залежить від кутового прискорення й визначається формулою aτ = εR.
Нормальне прискорення точки залежить від кутової швидкості тіла й визначається залежністю an = ω2R.
Рівномірний обертальний рух
Якщо кутова швидкість ω = const, то обертальний рух називається рівномірним.
Рівняння рівномірного обертання має вигляд φ = φ0 + ωt.
В окремому випадку, коли початковий кут повороту φ0 = 0, φ = ωt.
Кутову швидкість рівномірно обертового тіла 
можна виразити й так: 
, 
; де T - період обертання тіла, υ - частота обертання тіла; φ = 2π - кут повороту за один період.
Рівнозмінний обертальний рух
Визначення. Обертальний рух із змінною кутовою швидкістю називається нерівномірним.
Визначення. Обертальний рух з постійним кутовим прискоренням (ε = const), називається рівнозмінним.
Таким чином, рівнозмінне обертання тіла - окремий випадок нерівномірного обертальго руху.
Рівняння рівнозмінного обертання 
і рівняння, що виражає кутову швидкість тіла в будь-який момент часу 
, являють сукупність основних формул обертального рівнозмінного руху тіла.
Таблиця 1.1 - Основні формули кінематики
