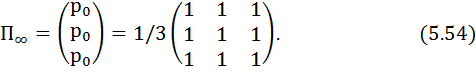Бұл бөлімде уақытта дискретті марковтық тізбектер түсінігі қадам-қадаммен енгізіледі. Біз бұл түсінікті қарапайым «кездейсоқ адасу» мысалында айқындаймыз.
Мысал: Студенттің кездейсоқ адасуы.
Бізді мас студент сырахана есігінен жатақхана есігіне жету турасындағы сауал қызықтырады. Сұрақты басқаша қояйық (5.2 сурет): 7 уақытша қадамда кездейсоқ адасулар студентті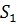 
кеңістіктік ахуалға әкелу ықтималдығы қандай я болмаса
P («кездейсоқ адасу» 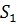күйіне n = 7 уақыт сәтінде алып келеді).
5.2 суретте бейнеленген ахуалда Марковтық тізбектің маңызды нышандары бар. Марковтық тізбек деп уақытта дискретті және ахуалы бойынша марковтық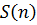 
процессі. Оның орындалуы 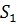күйінен 
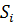күйіне апаратын көптеген жолдар болып табылады.
__________________________________
1 А. А. Марков (1856 - 1922) – орыс ғалымы.
5.2 Сурет. Студенттің кездейсоқ адасуы.
Марковтық тізбекті сипаттаудың бастапқы пункті ахуалдар көпшілігі болып табылады
Мұндағы N ахуалдар ықтималдықтарын n уақыт сәтінде бөліп таратудың натуралды және стохастикалық векторы
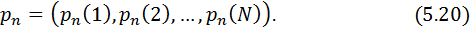
Марков тізбегін толықтай анықтау үшін бізге кез-келген n уақыт сәті үшін 
ықтималдықтарын есептеу тәсілін берy қалады. Ықтималдықтар анықтамасынан шығатыны
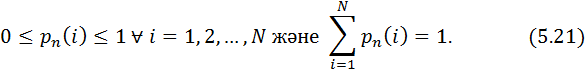
Ерекше маңызға бақылау басындағы ықтималдықтарды бөліп тарату ие, яғни бастапқы шарттар
Күйдің алмасуы өтпелі ықтималдықтармен сипатталады
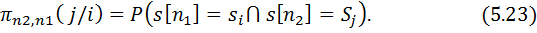
Бұл өтпелі ықтималдықтар келесі қасиеттерге ие:
1. n уақыт сәтінде ахуалдардың бірі әрдайым n1 сәтінде кез-келген Si -де жетеді
2. Шектік бөліп тарату, яғни n2 уақыт сәтіндегі j- ші ахуалдың ықтималдықтары
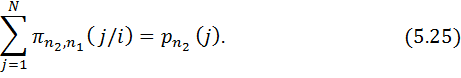
3. Өтпелі ықтималдықтар үшін рекурсивті формула (Колмогоров-Чэпмен теңдеуінің жеке жағдайы.)
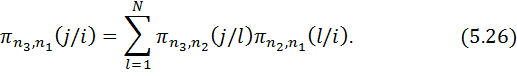
Колмогоров-Чэпменнің дискретті теңдеуі ықтималдықтар үшін «тізбектер қағидасының» трансформациясы болып табылады
Теңдіктің екі бөлігін де 
-ге көбейтіп, алатынымыз
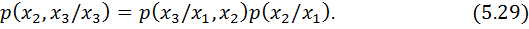
Барлық x2 -лер бойынша сомдап Колмогоров-Чэпмен теңдеуінің дискретті формасына келеміз
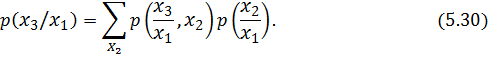
(5.30)-ды (5.26)-ға түрлендіргенде, біз шамалаймыз
Соңғы теңдеуді Марков процессі сипаттайды.
5.3.1 Анықтама. Марков процессі деп қазіргі мағлұм болған жағдайда өткен болашаққа әсер етпейтін процессті айтамыз.
Ескерту. Келтірілген мысалды мағлұм өткен дегеніміз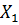 
стохастикалық айнымалысы, 
– мағлұм қазіргі, 
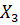- беймағлұм болашақ.
Марков тізбектері стационарлы, қалыпты және гомогенді болса оларды пайдалану оңайға соғады. Бұл үш түсінікті қарап шығайық.
5.3.2 Анықтама. Күйлер арасындағы өтпелі ықтималдықтар уақытша санақ нүктесінің таңдауынан тәуелсіз болса, Марков тізбегі гомогенді.
Осылайша, өтпелі ықтималдықтар уақыт l есебінің айырмашылықтары-на ғана тәуелді.
Бұл жағдайда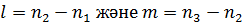 
үшін Колмогоров-Чэпмен теңдеуін (5.26) келесі түрде жазсақ болады
Бұл теңдеу векторлы-қатарлардың компонетті туындыларының векторлы-бағандарға қосындысы түрінде көрсетілуі мүмкін. Өтпелі ықтималдықтарды матрица түрінде жазып алып, (5.33)-ші теңдеуді матрицалық формада аламыз
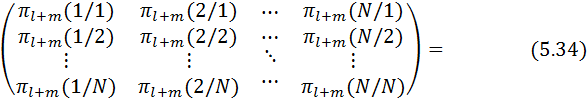
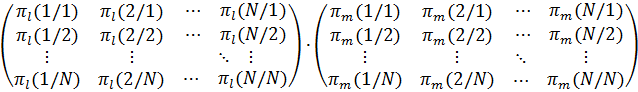
Бұл процесс өтпелі ықтималдықтар матрицасы арқылы бірінші қадамда басталуы мүмкін
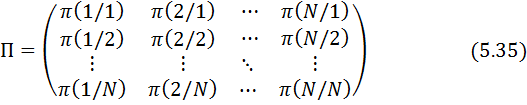
матрица II – қатар ықтималдықтарының саны 1-ге тең стохастикалық матрица екеніне назар аударайық.
p0 күйінің бастапқы бөлініп таралуына мұндай матрицалық түрлендіруді біршама мәрте қолдансақ, біз кез-келген n уақыт сәтінде pn ықтималдықтарының бөлініп таралуын аламыз
5.3.2 Теорема. Марковтың гомогенді тізбегі толықтай өтпелі ықтималдық-тар матрицасымен және күйлердің бастапқы бөлінуімен сипатталады.
Жоғарыда келтірілген тұжырымдарды ахуалдар кескіні (5.3 сурет) арқылы жалпылауға болады. Бұл жерде түйіндер ахуалдарға сәйкес келеді, ал олардың арасындағы жолдар ахуалдар арасындағы өтулерге сәйкес. Әрбір жолға өтпелі ықтималдыққа тең салмақ жазылған. Осылайша, ахуалдар кескіні өтпелі ықтималдықтар матрицасы турасында толық мағлұмат береді.
5.3 Сурет. Марковтың гомогенді тізбегінің ахуалдар кестесі.
Мысал: Студенттің кездейсоқ адасуы (жалғасы).
Кездейсоқ адасулар (5.2 суретті қараңыз) 5.4 суретте ахуалдар кестесі кейіпінде көрсетілген.
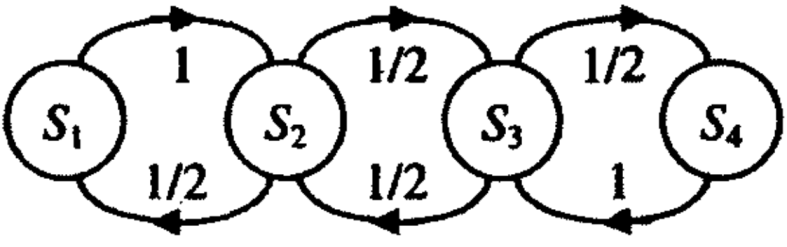
5.4 Сурет. Студенттің кездейсоқ адасуы үшін ахуалдар кестесі.
Ахуалдар кестесіне өтпелі ықтималдықтар матрицасы сәйкес келеді
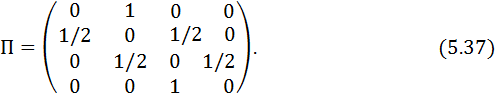
5.2 сурет бойынша, ахуалдардың бастапқы бөлінуі келесідей
Кездейсоқ адасудың нәтижесінде студент 7-ші уақытша қадамда жатақхананың есігінің алдына барып қалу ықтималдығы, 7-ші 
қадамдағы ахуалдар векторының бірінші компонентасы арқылы анықталады. (5.36) бойынша
Компьютер жәрдемімен шығарылған есептеулер
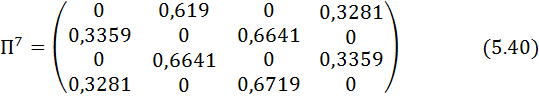
Мұнан шығады
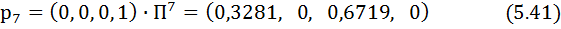
және ізделіп отырған ықтималдық тең
Марковтық тізбектің маңызды жеке жағдайы ахуалдарды бөліп таратудың бақылау уақтысынан тәуелсіздігі болып табылады.
Анықтама 5.3.3. Егер ахуалдарды бөліп тарату уақытта тұрақты болса Марковтың гомогенді тізбегі стационарлы. Бұл жағдайда бастапқы бөліп тарату өтпелі ықтималдықтардың матрицасының меншікті векторы болып табылады, яғни
Ескерту. Егер ахуалдарды бөліп тарату векторы компоненттер сомасы 1-ге тең стохастикалы векторы болып табылса меншікті вектордың компонент сомасы сондай-ақ 1-ге тең.
Марковтың тізбегі стационарлы болуы үшін (5.43) орындалуы міндетті.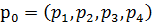 
болсын, онда
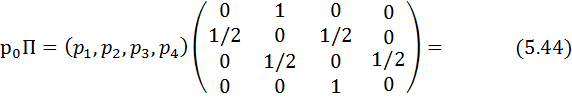
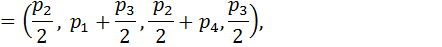
(5.43) және (5.45) шарттарды қолданып, ахуалдардың стационарлы бөлінулерін табамыз
Рекурсивті қатынастан (5.36) келесі маңызды сауалдар туындайды: «Ұзақ уақыт өткеннен» соң не болады, яғни 
? Ахуалдардың стационарлы бөліп таратылуы орнатылады ма? Стационарлы бөліп таратуға ұқсас нәрсе барма, мәселен, ахуалдарың екі тұрақты бөлініпп таралуы?
Анықтама 5.3.4. Марковтың гомогенді тізбегі тұрақты деп аталады, егер:
● Шекті матрица
бар болса, сонымен қатар, шекті матрицаның барлық N қатарлары өзімен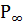 
шекті бөліп таратылуын ұсынса;
● Шекті бөліп тарату кез-келген тұрақты Марковтық тізбектің ахуалдарынің ықтималдықтарын жалғыз стационарлы бөліп таратушы болып табылады;
● Егер П n матрицасының қандай-да бір бағанының барлық компоненттері нөлден айырықша болатын қандай-да бір натурал n бар болса, Марковтық тізбек әрдайым тұрақты.
5.3.4 анықтаманың соңғы тұжырымы келесі суреттемеге тең: егер қандай-да бір n қадамда кез-келген бастапқы күйден жете алатын бір ахуал болса, Марковтың тізбегі тұрақты.
Мысал: Кездейсоқ адасулар (жалғасы).
Студенттің кездейсоқ адасу мысалын қарап шығайық және бұл адасуларға сай Марковтың тізбегі тұрақты ма екенін айқындайық.
Өтпелі ықтималдықтар матрицасының (5.37) n уақытша қадамдардың санының жұп және жұп емес екендігіне байланысты екі шекті ахуалы бар
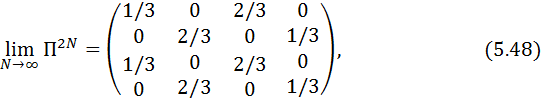
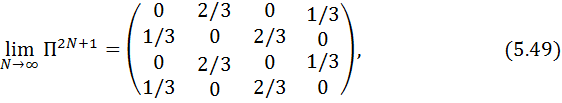
сондықтан, бұл жағдайда Марковтың тізбегі тұрақты болып табылмайды.
Сонымен қатар, 5.3.4 анықтаманың соңғы шарты да орындалмайды, себебі әр қадамда барлық жұп ахуалдар тақ ахуалдар тарапына өтеді және керісінше (5.2 суретті қараңыз).
Ескерту. Егер біз бастапқы бөліп таратуды таңдасақ, мәселен (5.46)-дағы р 0, онда кез-келген уақыт қадамында кез-келген ахуалға жетуге болады.
Мысал: Үш ахуалды Марковтық тізбек.
Марковтық тізбек ахуалдар кестесімен берілген болсын (5.5 сурет)
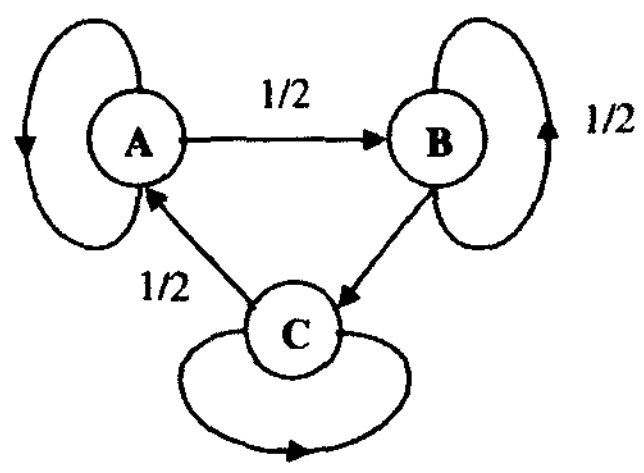
5.5 Сурет. Ахуалдар кестесі.
1. Өтпелі ықтималдықтар матрицасын құрыңыз.
2. Марковтың тізбегі стационарлы екенін көрсетіңіз. Сонымен бірге,
ахуалдардың бастапқы бірқалыпты бөліп таралуынан бастаңыз.
3. Марковтың тізбегі тұрақты екенін көрсетіңіз.
4. Шекті өтпелі матрицаны құрыңыз.
Шешімі.
1. Өтпелі ықтималдықтар матрицасы
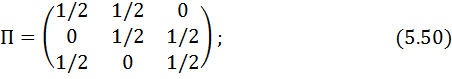
2. Стационарлық.
Ахуалдардың бастапқы бөліп таратылуы бірқалыпты болғандықтан
Сонымен бірге, (5.4) шарт орындалады
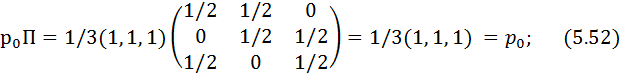
3. Марковтың тізбегі тұрақты, себебі
П 2 үшін де 5.3.4 анықтаманың соңғы шарты орындалады;
4. Шекті өтпелі матрица.
Марковтың тізбегі тұрақты болғандықтан, 5.3.4 анықтаманы қолданайық, ондағы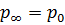 
және 5.51-ден шығатыны
