ТАСЫМАЛДАУ
Кіріспе
4-ші бөлімде ақпараттың екі байланысты дереккөзі қарастырылған болатын. Байланысты дереккөздер үшін бірлескен, өзара және шартты пар оқиғалар (символдар) ақпараттары деген негізгі түсініктер енгізілген болатын. Олардың негізінде біз ақпараттың іргелі түсініктеріне келдік – бірлескен, өзара және шартты энтропия(4.3 кестені қараңыз). Бірлескен және шаррты энтропиялар ықтималдықтар теориясында да ұқсастықтары бар және екі дереккөздің барлық жұп оқиғаларының бірлескен және шартты ақпараттардың математикалық күтімі ретінде анықталатыны сол жерде көрсетілген.
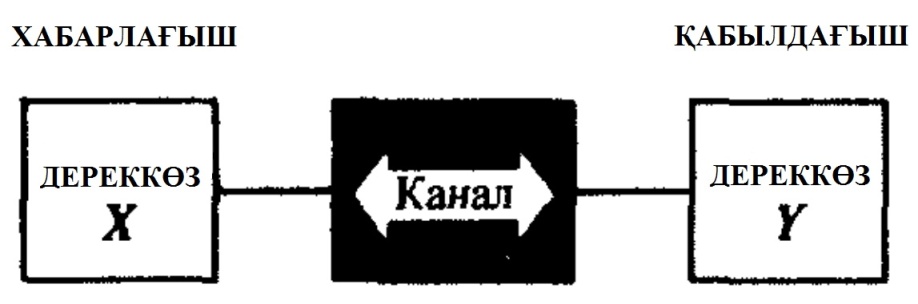
7.1 Сурет. Хабар беру үлгісі
Біз бұл пікірді бірлескен энергияға зер салу арқылы жалғастырамыз. Ақпарат тасымалдау каналдарын сипаттау үшін екі байланысты дереккөз тұжырымдама- сын қолданамыз. 4 бөлімде көрсетілген түсініктер арқылы жадсыз каналдар арқылы ақпарат тасымалдау жүйесін толықтай сипаттай алады екенбіз. Нәтиже- сінде біз канал арқылы ақпарат тасымалдау мүмкіндігін яғни каналдың өткізгіштік қабілетін бағалай аламыз.
Байланыс каналының Шеннондық үлгісінде бірінші дереккөздің(хабарлағыш) мағлұматы канал арқылы қабылдағышқа тасымалданады және пайдаланушыға беріледі. Пайдаланушы үшін қабылдағыштың шығысы ғана маңызды яғни қабыл-дағыштың өзі ақпараттың қайнар көзі болып табылғандықтан байланысты дерекөздер үлгісі “Хабарлағыш – Канал – Қабылдағыш” тізбегіне толық жарамды.
Егер ақпарат тасымалдау жүзеге асып жатса, бірінші дереккөз символдары екінші дереккөз символдарына әсер етуі тиіс. Мысал ретінде екілік жадсыз симметрилы каналдарды қарастырамыз.
Екілік симметриялы канал
Екілік симметриялы канал (ЕСК) екі жадсыз дискретті дереккөздердің ең қарапайым әрекеттесу мысалы болып табылады. Ал аддитивті ақ гаусстық шумен (ААГШ) канал арқылы екілік дискретті ақпарат тасымалдау үлгісі болып табылады.
Ескерту. Кедергіге тұрақты кодтау алгоритмдерінің нәтижелілігін тексері уақтысында, байланыс каналдарын Монте-Карло тәсілімен есептеу және модельдеу үшін каналдардың дискретті үлгісі ұтымды қолданылады.
Екілік симметриялы канал диаграммалы өткел арқылы суреттеледі (7.2 сурет). Диаграммада Х дереккөзінің екілік символдарының (0,1) Ү дереккөзінің екілік символдарына мүмкін өтулері ұсынылған. Әр өткелге өту ықтималдығы жазылған.
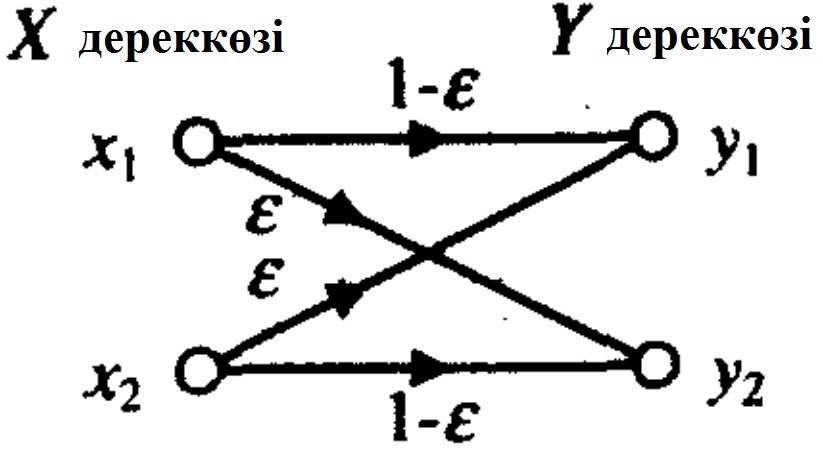
7.2 Сурет. Екілік симметрилы канал арқылы мағлұмат тасымалдау диаграммасы.
7.2 суреттен қате өтулерге ɛ ықтималдығы сәйкес екенін көреміз, сондықтан, әдетте айтылуынша, екілік мағлұматты ЕСК арқылы тасымалдағанда, қате ɛ ықтималдығымен болады. Канал матрицасы өту диаграммасының эквиваленті болып табылады. Ол өту ықтималдықтарын қамтамасыз етеді және әр қатарының барлық элементтерінің жиынтығы бірлікке тең схоластикалық матрица болып табылады.
Кіру әліпбилі канал матрицасы, M xi рәмізінен және кіру әліпбиінен тұратын, N yj символынан тұратын, барлық өту ықтималдықтарын P(yj / xi) қамтамасыз етеді және келесі түрде болады
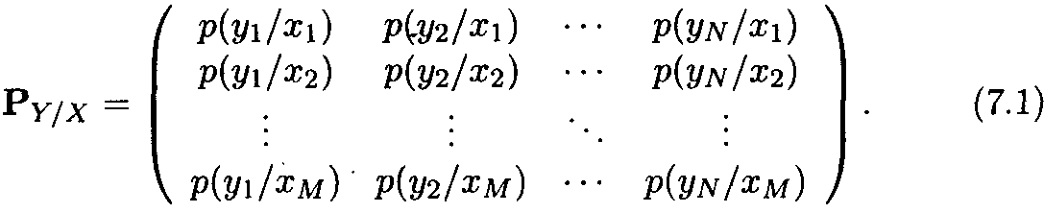
ЕСК жағдайында
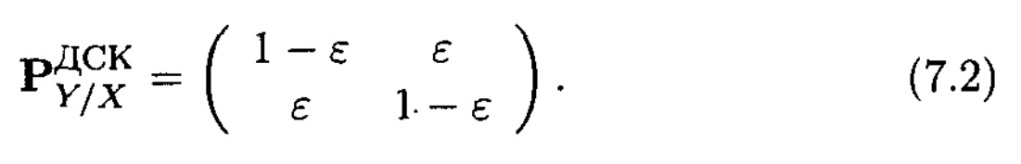
Өтулер симметриясынан канал кірісіндегі рәміздердің бірқалыпты бөлінуі өз кезегінде шығу символдарының бірқалыпты бөлінуіне алып келетіні белгілі.
Кіру символдарының бірқалыпты бөлінуін шамалап, барлық мүмкін жұп оқиғалардың шартты және өзара мағлұматтарын жазып аламыз. ЕСК үшін
Мұнан шығады
Үш ерекше жағдайды қарастырамыз
1. ɛ = 0 (қатесіз тасымалдау)
I (x1 ; y1) = I (x2; y2) = 1 бит.
Басқа өзара мағлұматтар жоқ, себебі өзара рәміздердің жұптары (x1, y2) және (х2, y1) ешқашан пайда бола алмайды. Ақпарат X дереккөзінен Ү дереккөзіне ысырапсыз тасымалданады.
2. ε= 1/2. Барлық жұп рәміздер (xi, yj) үшін
I(xi; yj) = log2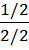 
бит = 0.
Х және Ү дереккөздері тәуелсіз болып табылады. Ақпарат тасымалдау болып жатқан жоқ.
3. ɛ = 1. Бұл жағдайда я әлдеқандай ықтималдықтар алмасып кеткен я болмаса біз бір жерде толық қателестік. Бұл ақиқатты ұшыратқан уақытта және қабылданған yi символдарын инверттеген соң, біз бірінші жағдайға қайта ораламыз.
Нәтижесінде шартты I(yi / xj) = I(y1 / x1) және өзара I(yi; xj) = I(y1; x1) мағлұматтарының тәртібін ЕСК-да ɛ ықтималдық функциясының қатесі ретінде қарастырамыз.
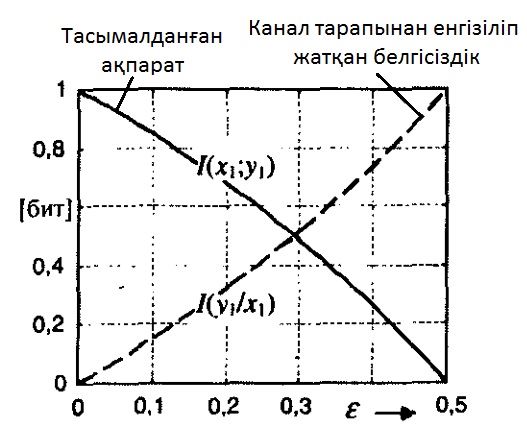
7.3 Сурет. Шартты I(y1 / x1) және өзара I(y1; x1) мағлұматтары
Шартты I(y1 / x1) мағлұматын канал тарапынан енгізіліп жатқан белгісіздік деп, ал өзара I(y1; x1) мағлұматын канал арқылы тасымалданып жатқан ақпарат ретінде қарастыруға болады. Бір ғана ɛ=0 екілік рәмізін тасымалдағанда ақпарат ысырапсыз жетіп барады, сол себепті I(y1 / x1)=0, ал I(y1; x1)=1 бит. ɛ-нің қате ықтималдығы жоғарылауы себепті, канал тарапынан енгізіліп жатқан белгісіздік өседі, ал тасымалданып жатқан ақпарат, керісінше, азаяды. ɛ=0,5 болған жағдайда, ақпарат тасымалдау жүрмейді, сондықтан I(y1 / x1)=1 ал I(y1; x1)=0. Шартты I(y1 / x1) және өзара I(y1; x1) ақпараттар қосындысы ɛ-ге тәуелді емес және әрдайым бір битке тең.
Ақпарат тасымалдау
Өткен бөлімде бөлек жұп оқиғаларды қарастырғаннан соң, ақпарат тасымалдау үлгісіне қайта оралайық. 7.4 суретте негізгі жағдаят көрсетілген.
Каналды өтпелі ықтималдықтар жәрдемімен суреттеу ақыр аяғында бірлескен жұп оқиғалар ықтималдықтарына әкеледі. Осы тұрғыдан алғанда, екі дереккөз де ақпарат тасымалдау үлгісінде бірдей мәнге ие, сол себепті ақпарат тасымалдау бағытын ескере отырып дереккөздерді хабарлағышқа және қабылдағышқа бөлу қазір және мұнан былай мағынасыз.
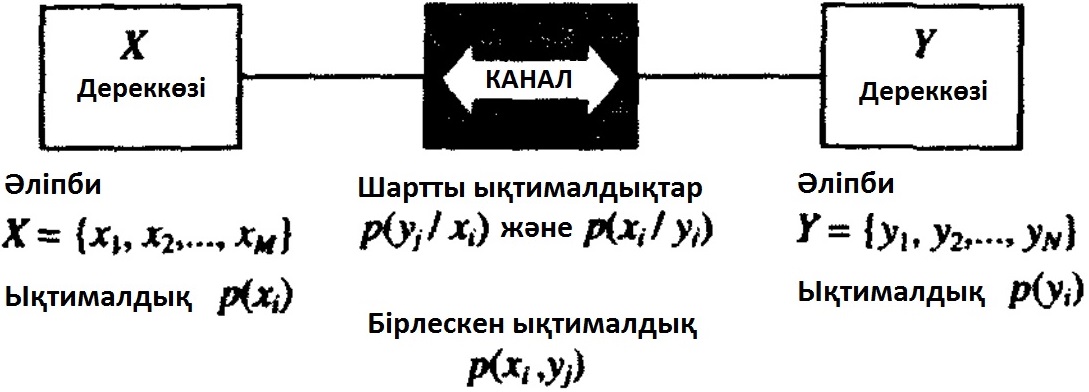
7.4 Сурет. Каналмен байланысқан екі жадсыз дискретті дереккөз.
4 бөлімде (4.3 кестені қараңыз) екі дереккөздің бірлескен энтропиясы барлық мүмкін жұп оқиғалар ақпаратының математикалық күтімі ретінде анықталған
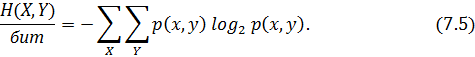
Шартты энтропия да дәл осылай анықталады
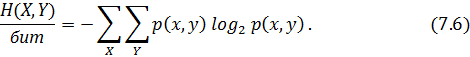
Мұнан шығады
H(X, Y) = H(Y) + H(X/Y) = H(X) + H(Y/X) (7.7)
және
әрі, теңдік белгісі тек қана тәуелсіз дереккөздер үшін қойылады.
Каналмен байланысты екі дереккөз жағдайында, бірлескен белгісіздік төмендейді, себебі бір дереккөздің оқиғасы басқа дереккөз оқиғасын шамалауға ерік береді. Ақпарат теориясының тұрғысынан алғанда, белгісіздіктің төмндеуі дереккөздер арасындағы мағлұмат алмасуды тұспалдайды. Ұқсас ой жүгірте отырып канал арқылы тасымалданып жатқан ақпараттың орташа мәні барлық жұп оқиғалардың өзара мағлұматтарының математикалық күтімі ретінде анықталады деген шешімге келеміз.
Х және Ү екі жадсыз дискретті дереккөздері алмасып жатқан мәліметтің орташа мәні тең болады
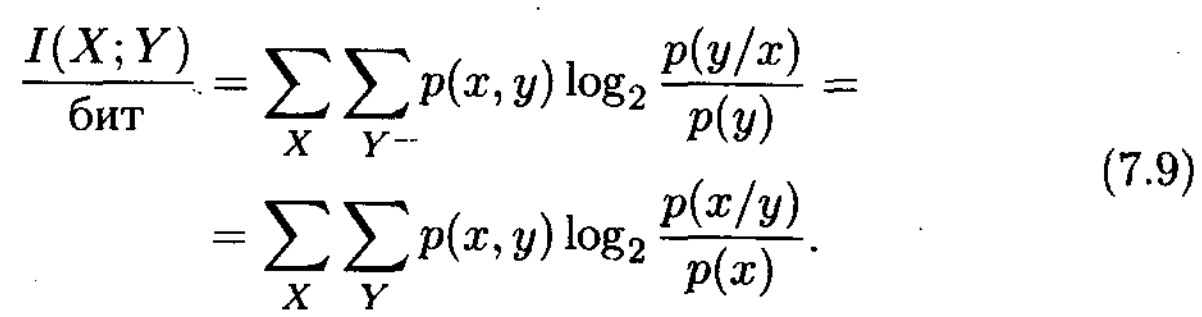
Ескерту. Теңдіктің сол жағындағы “минус” таңбасына және оң жақ алдындағы “плюс” таңбасына назар аударыңыз.
Тасымалданған ақпарат анықтамасынан шығатыны
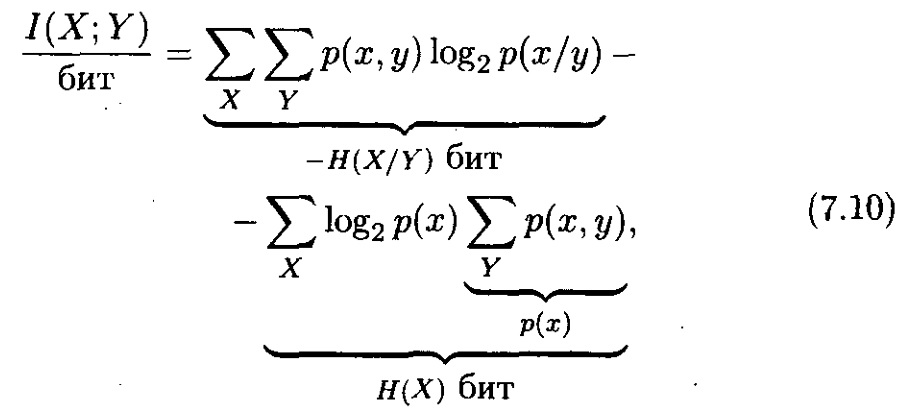
және сол себепті,
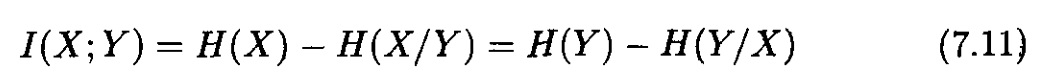
Бұл жерде қайтадан энтропияның аксиоматикалық мазмұны турасындағы анықтамасы хақында сауал туындайды. “Сын тас” ретінде әуелі келесі тұжырымның әділ екенін дәлелдейміз.
7.3.1 Теоремасы. I(X; Y) тасымалданып жатқан ақпараты әрдайым теріс емес мәнде, әрі ол тек қана тәуелсіз Х және Ү дереккөздері үшін ғана нөлге тең
I(X; Y) ≥ 0. (7.12)
Дәлел.
Дәлелдеу үшін I(X; Y) анықтамасын негізге аламыз және үш тәсіл қолданамыз. Біріншіден, натурал логарифм функциясын бағалаймыз (2.19). Екіншіден, қауымдастықты шектемей тек ықтималдығы нөлден өзгеше рәміздер жұбын ғана қарастырамыз. Үшіншіден, (2.19)-дағы логарифмдік функцияның аргументінде есептеуіш және аяндауыштың орындарын алмастыру логарифмдік функцияны минус 1-ге көбейткенге эквивалентті, сол себепті бізге теңсіздіктің әділ екенін дәлелдеудің өзі жетеді
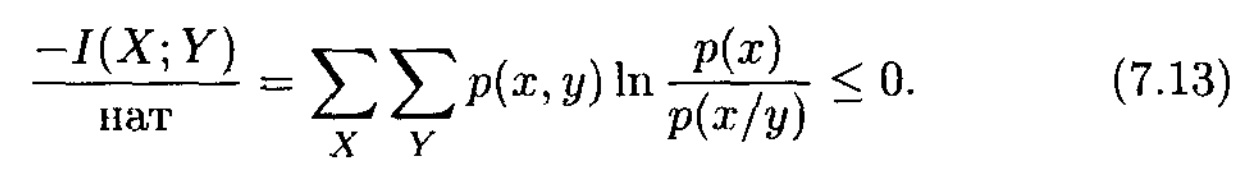
Бізге қойылған шектеудің салдарынан, қосындылар p(x, y) ≠ 0 үшін (x, y) жұптарынан ғана алынады,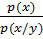 
логарифмдік функциясының аргументі әрдайым нөлден өзгеше оң мәнге ие, сондықтан (2.19) бағасын қолданамыз
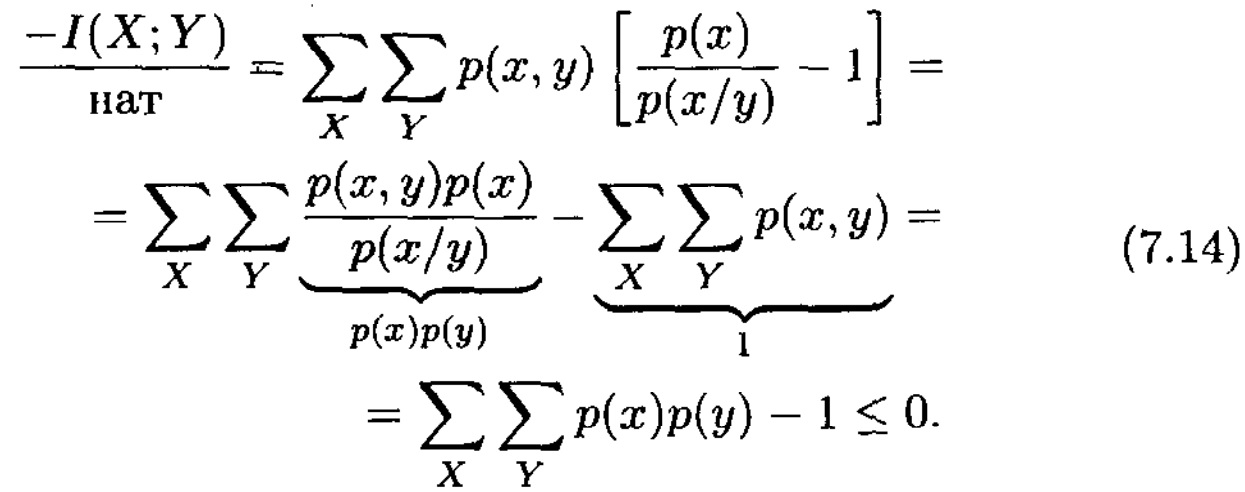
(7.12) орындалмаған жағдайда, ақпарат тасымалдау энтропияны төмендетпеген болар еді (яғни дереккөз айқындығы жоғарыламас еді).
Тасымалданған ақпарат әрдайым теріс емес және (7.1) және (7.2) теңдіктері үнемі әділ екендігі, келесі тұжырымның әділ екендігін тағы да дәлелдейді:
Кез-келген шектеу дереккөз белгісіздігін жоғарылата алмайды
H(X) ≥ H(X/Y). (7.15)
Бірлескен энтропия өзінің максимумына дереккөздер тәуелсіз болған жағдайда ғана жетеді
H(X, Y) ≤ H(X) + H(Y). (7. 16)
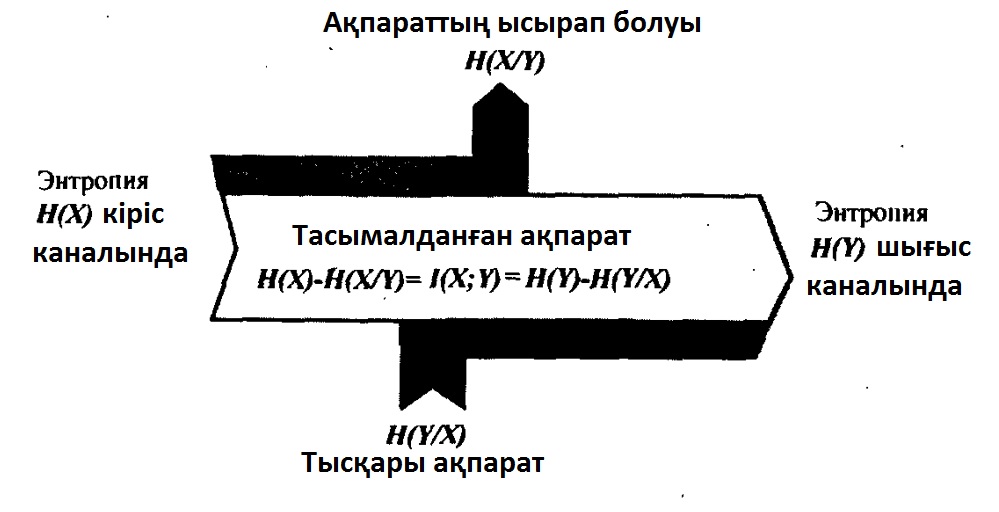
Табылған тәуелділіктерді ақпараттар тасқыны диаграммасы жәрдемімен көрнекі айқындауға болады(7.5 сурет). Диаграмма шартты H(X/Y) және H(Y/X) энтропияларының мағнасын анықтауға септігін тигізеді.
7.5 Сурет. Ақпараттық тасқын диаграммасы
H(X/Y) – Х дереккөзінің жіберілген рәміз белгісіздігінің орташа өлшемін Ү дереккөзінің қабылдағышының символдары мәлім болған жағдайда ғана анықтайды, яғни қабылдағыштың қалған белгісіздігін анықтайды. H(X/Y) үлкендігін кейде ақпарат “жайылуы” деп те атайды, себебі H(X) энтропиясын
Х, H(X) = 1(X; X) дереккөзінің меншікті ақпараты деп те интерпретациялауға болады. H(X/Y) = 0 шусыз каналында ақпарат Х дереккөзінен Ү дереккөзіне және кері қарай ысырапсыз тасымалданады (“жайылусыз”). Егер канал толығымен шулы болса H(X/Y) = H(X) болады және ешқандай ақпарат тасымалдау жүзеге аспайды (барлық ақпарат “ысырап” болады).
H(Y/X) – жіберілген мәлім символдарда қабылданған символдың орташа белгісіздігін анқтайды, сондықтан оны “тысқары” шулы ақпарат деп атайды.
Шулы канал арқылы ақпарат тасымалдауды белгісіздіктің төмендеуіне әсері тиетін тәжірибелер сериясы деп қарастыруға болады. Ақпараттар теориясының тұрғысынан алғанда канал шулардың қайнар көзі болып табылады.
Мысал: Екілік симметриялы канал (ECK) арқылы ақпарат тасымалдау.
ЕСК мысалындағы (7.2 сурет) I(x; y) төбесінің физикалық мағынасын айқындаймыз. Екілік симметриялы канал үшін
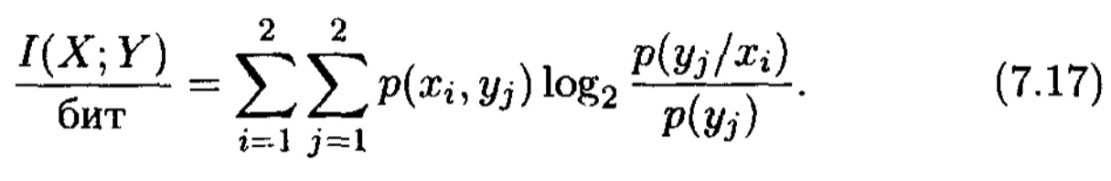
Көріп тұрғанымыздай, I(X; Y) екі ғана параметрге байланысты – каналдағы қате ықтималдығынан және х1 символының р(х1) каналының шығысында пайда болу ықтималдығынан. Сонымен қатар келесі өрнектер орындалады
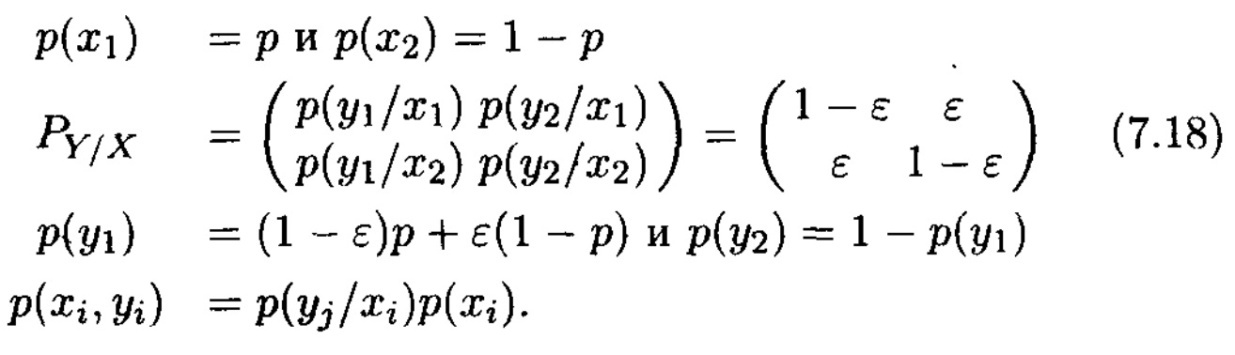
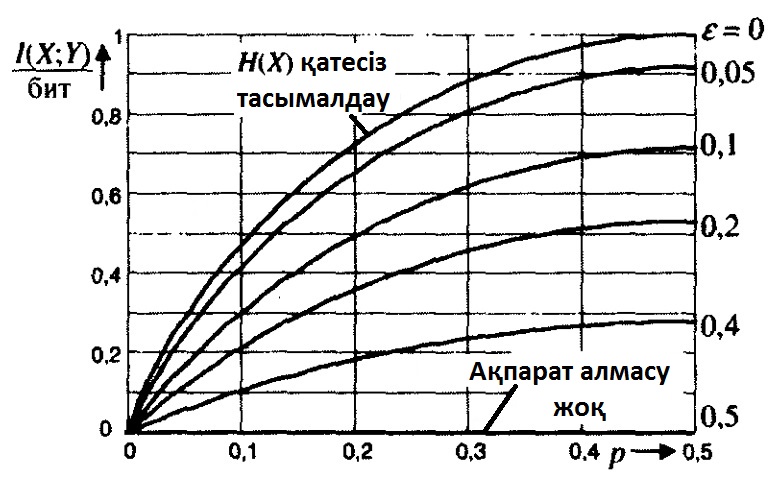
7.6 Сурет. р каналының кірісіндегі символ ықтималдығының
түрлі мәндері үшін екілік симметриялы канал арқылы
ɛ қате ықтималдығымен ақпарат тасымалдау.
Түрлі ɛ және р болғандағы I(X; Y) есептеулерінің нәтижесі 7.6 суреттегі қисық ɛ = {0.05, 0.1, 0.2, 0.4, 0.5} түріндегі I(X; Y) = f(p) отбасы кейпінде көрсетілген. Шусыз каналда ɛ = 0 ақпарат тасымалдау қатесіз жүзеге асады және I(X; Y) мағлұматы бұл жағдайда канал кірісіндегі Н(х) энтропиясына тең болады. Шу дәрежесінің көтерілуіне байланысты, ɛ қате ықтималдығы жоғарылайды, ал тасымалданған ақпарат саны төмендейді, сонымен қатар салыстырмалы төмен ɛ = 0,05 дәрежесі I(X; Y) елеулі төмендеуіне әкеледі. Толықтай шулы ɛ = 0,5 каналда ақпарат тасымалдау мүмкін емес.
Түртіп өткен жөн, ɛ-нің назар аударған мәндерінде I(X; Y) мәліметі елеулі түрде канал кірісіндегі р ықтималдығына тәуелді. p = 1/2 болған жағдайда канал арқылы ақпарат максималды түрде тасымалданады. 7.5 бөлімде жаңа түсінік енгізіледі – каналдың өткізу қабілеті, I(X; Y)-тың бұл қасиеті толық түрде қарастырылады.
Мысал: Байланысты дереккөздер.
Біз энтропияның мағынасын сандық мысалда қосымша айқындап өтеміз. Бұл үшін біз барлық бізді қызықтыратын төбелері оңай есептелінетін байланысты дереккөздер конструкциясын ұсынамыз.
7.1 кестеде жадсыз дискретті Z дереккөзі алфавиттегі символдармен {0, 1, 2, 3} және символдардың сәйкес ықтималдықтарымен берілген. Әрбір zi сиволы бірінші биті xi және екінші биті yi болатын екілік кодпен кодталады. Біз бұл биттерді екі байланысты Х және Ү дереккөздерінің символы ретінде интерпретациялаймыз.
7.1 Кесте. Zдереккөзі және оның екілік кодталуы
Келесі тапсырмаларды орындаңыз:
1. Х және Ү дереккөздерін сипаттаңыз;
2. Х және Ү дереккөздерінің арасына Х дереккөзі канал кірісі болатын, ал Ү дереккөзі оның шығысы болатын байланысты канал үлгісінің моделінде орнатыңыз;
3. 2 тапсырма үшін ақпараттар тасқыны диаграммасын келтіріңіз және осы диаграмма үшін энтропиялардың сандық мәндерін табыңыз;
4. Z дереккөзінің энтропиясын табыңыз;
5. 2 және 3 тапсырмаларды Ү дереккөзін каналдың кірісі деп есептеп орындаңыз.
Шешімі.
1. Х және Ү дереккөздерін сипаттаудан бастайық. Екі дереккөзде жадсыз дискретті дереккөздер болып табылады. 7.1 кестені қолданып олардың әрбірі үшін 0 және 1 сиволдарының ықтималдықтарының бөлінуін табамыз
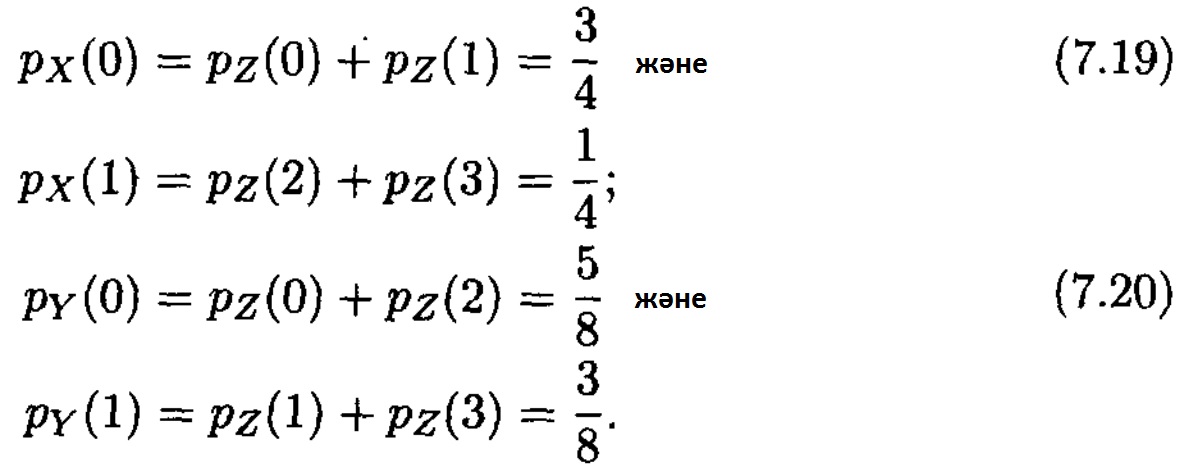
(2.34) сәйкес, дереккөздер энтропиялары тең
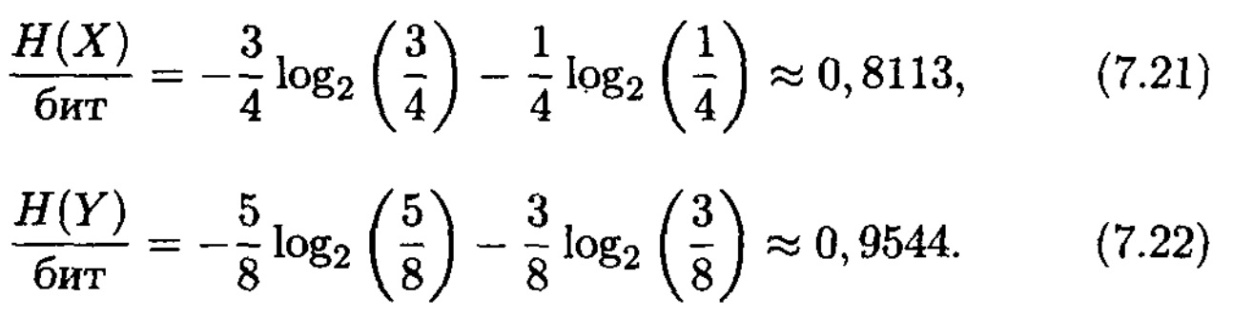
2. Канал үлгісі өзімен кірісінде x1 және х2 һәм шығысында y1 және y2 символдары бар екілік каналды ұсынады. Канал p (yj /xi ) ықтималдықтарынан тұратын өтпелі ықтималдықтар матрицасымен(7.1) берілген болуы мүмкін. (7.19), (7.20) және 7.1 кестеден келесі өрнектер шығады
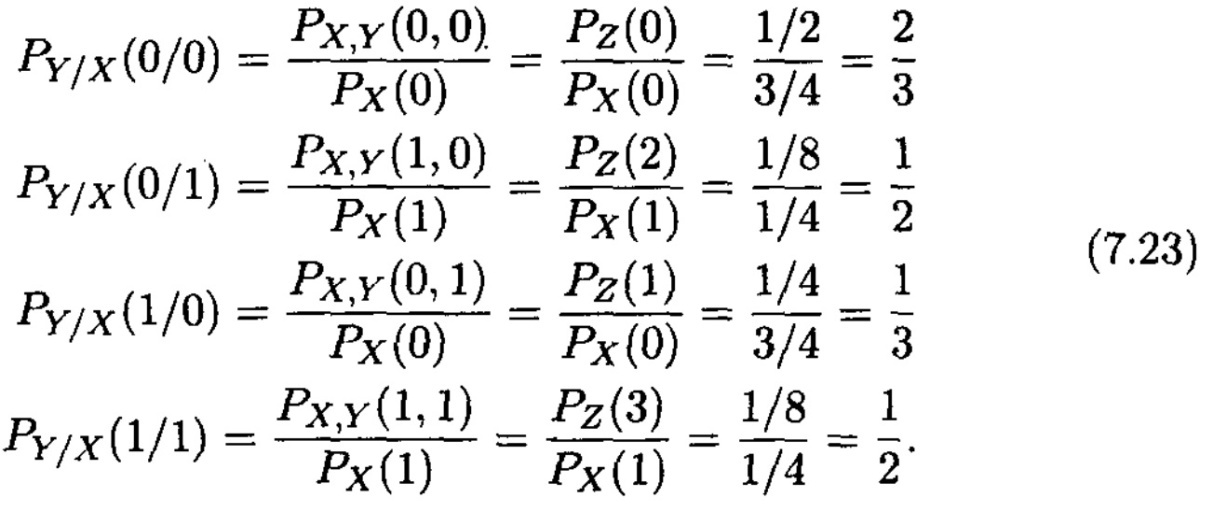
Нәтижесінде каналдың өтпелі ықтималдықтар матрицасы шығады
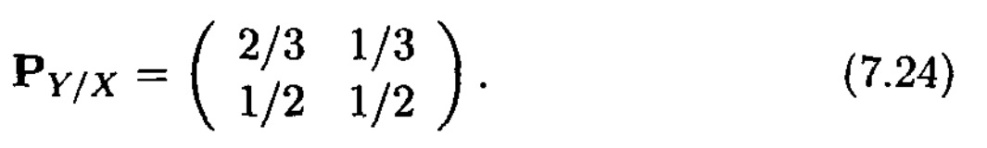
Ескерту. Күткеніміздей, матрица ықтималды болып табылады, өйткені оның әр қатарындағы ықтималдықтар қосындысы бірге тең.
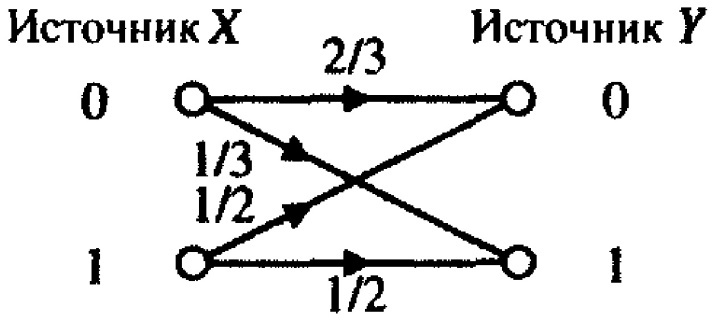
7.7 Сурет. Екілік канал.
Канал диаграммасы өту ықтималдықтарымен 7.7 суретте көрсетілген. Оның 7.2 суреттегі диаграммамен ұқсастықтарын байқауға болады. Бірақ, біздің мысалда енді каналдағы қателер турасында айтуға болмайды.
3. Ақпараттық тасқындар диаграммасын құру үшін H(Y/X), H(X/Y) және I(X;Y) төбелерінің мәндері қажет. Белгілі өту ықтималдықтарымен H(Y/X) есептеп алуға болады
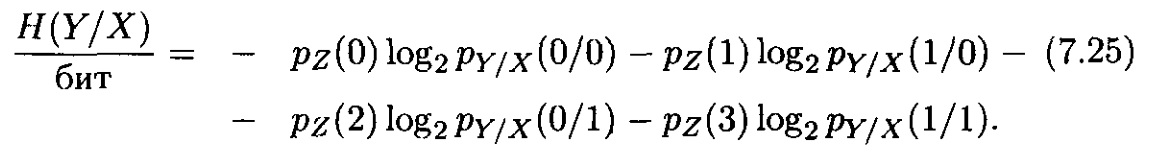
Сандық мәндерін қойып тапқанда
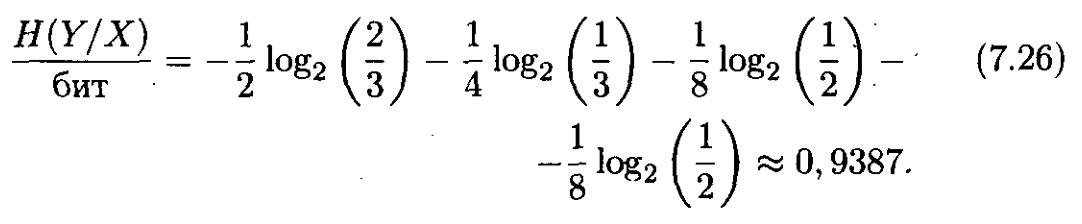
I(X;Y) и H(X/Y) төбелерін (7.11) тапса болады.
Ақпараттық тасқындар диаграммасы 7.8 суретте ұсынылған.
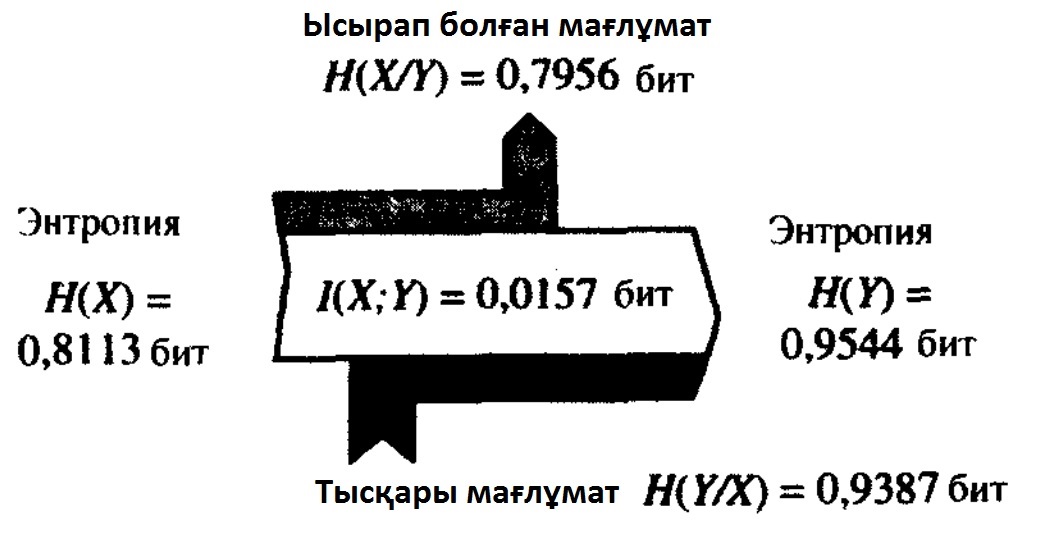
7.8 Сурет. Байланысты дереккөздердің ақпараттық
тасқындар диаграммасы.
4. Z дереккөзінің энтропиясы
Алынған нәтижелерге келесі интерпретацияны беруге болады. Z дереккөзінің энтропиясы келесі Х және Ү екілік дереккөздерінің бірлескен энтропиясына тең болады. Н(Х) дереккөзінің энтропиясы 0,8113-ге тең, қалған 0,9387 битті (7.7) сәйкес H(Y/X) шартты энтропиясы енгізеді.
5. Екінші тапсырмаға ұқсастырып, табамыз
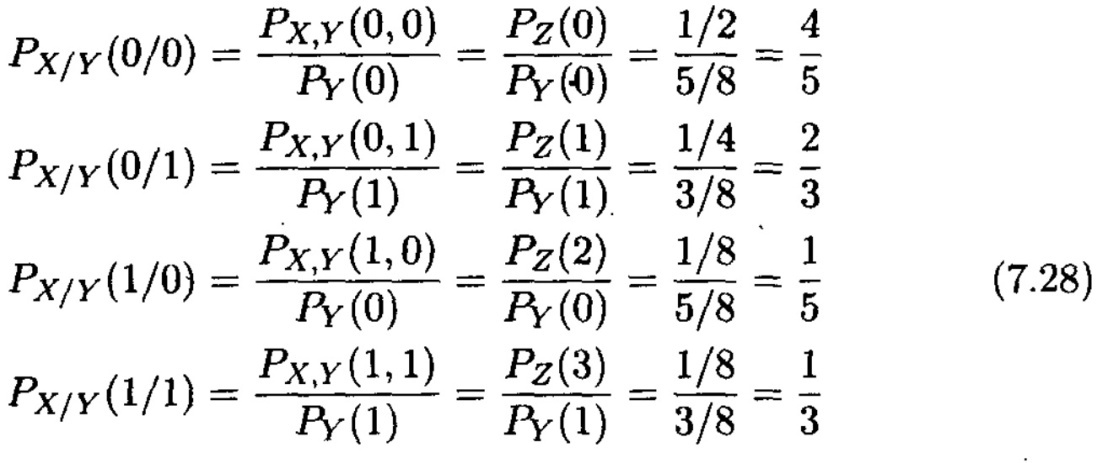
және матрица каналын аламыз
Канал және ақпараттық тасқындар диаграммасы 7.9 және 7.10 суреттерде көрсетілген.
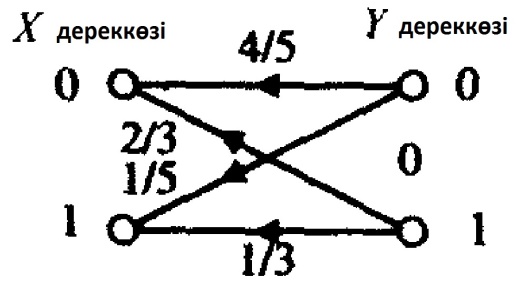
7.9 Сурет. Екілік канал
7.10 Сурет. Ақпараттық тасқындар диаграммасы.
Орытынды
Алдыңғы бөлімдерде қарастырылған барлық анықтамалар мен төбелер 7.2 және 7.3 кестелерде жалпыланған. Ықтималдықтар теориясынан ақпараттар теориясына өткелдерге ерекше назар аудару қажет.
Бұл өткелдерде жадсыз дискретті дереккөздердің шығыс символдары кездейсоқ тәжірибелердің нәтижесі ретінде қарастырылады. Бұл нәтижелер-дің ықтималдықтарына сәйкес әр символға оның пайда болу логарифдік ықтималдығына шамалас бірсыпыра ақпараттық өлшем меншіктеледі. Символдар ықтималдықтарын стохастикалық айнымалы деп қарастыруға болатынын ескере өткен жөн.
Символдардың ықтималдықтарынан олардың ақпараттық мазмұнына өткенде ықтималдықтар теориясында аналогы жоқ жаңа өлшем енгізіледі – бірлескен (х, у) жұп оқиғаларды анализдеуде пайда болатын, өзара ақпарат. Өзара ақпарат р(у) априорлы ықтималдығына у р(у/х) символының апостери-орлы қарым-қатынасының логарифмі қарастырылады және екі оқиғаны байланыстырушы ақпараттық өлшем ретінде қызмет етеді.
Дереккөздерді сипаттау үшін дереккөз түрлендіретін символдар ақпаратының орташа мәні қолданылады. Осылайша, жеке оқиғалардың (символдардың) ақпарат санының немесе жұп оқиғалардың математикалық күтімі ретінде энтропия түсінігі енгізіледі. Сонымен қатар, өзара ақпарат өте маңызды рөл ойнайтынын ескере кетеміз. Оның математикалық I(X;Y) күтімі тасымалданып жатқан ақпараттың өлшемі болып табылады және Х және Ү дереккөздерінің байланысын сипаттайды, яғни байланыс каналы арқылы дереккөздер алмасып жатқан ақпараттың орташа санын бейнелейді. I(X; Y) өлшемінің негізгі түсініктері келесі бөлімдерде толық әшкереленеді.
7.2 Кесте. Х және Ү жадсыз дискретті дереккөздері х € X = {х1, х2,....,хм}
және у € Y = {у1, у2,...., уN} символдарымен.
7.3 Кесте. Х және Ү жадсыз дискретті дереккөздерін х € X = {х1, х2,....,хм}
және у € Y = {у1, у2,...., уN} символдарымен “орташа” сипаттау.
