Ш.10 Местная устойчивость листа настила между продольными ребрами, продольных полосовых ребер, свесов поясов тавровых продольных и поперечных ребер должна быть обеспечена согласно 8.45 и 8.47, а стенки тавровых ребер - согласно приложению X. При этом следует выбирать наиболее невыгодную комбинацию напряжений от изгиба ортотропной плиты между главными балками и совместной ее работы с главными балками пролетного строения.
Ш.11 Общая устойчивость листа настила, подкрепленного продольными ребрами, должна быть обеспечена поперечными ребрами.
Момент инерции поперечных ребер Is (по Ш.3) сжатой (сжато-изогнутой) ортотропной плиты следует определять по формуле
| (Ш.11) |
где α - коэффициент, определяемый по таблице Ш.3;
ψ - коэффициент, принимаемый равным: 0,055 при k = 1; 0,15 при k = 2; 0,20 при k ≥ 3;
k - число продольных ребер рассчитываемой ортотропной плиты;
L - расстояние между стенками главных балок или центрами узлов геометрически неизменяемых поперечных связей;
l - расстояние между поперечными ребрами;
Isl - момент инерции полного сечения продольного ребра (по Ш.3);
σ cr - действующие напряжения в листе настила от совместной работы ортотропной плиты с главными балками пролетного строения, вычисленные в предположении упругих деформаций стали;
σ x.cr.ef - напряжение, вычисленное по таблице 8.23 по значению σ x.cr = σ xc.
Таблица Ш.3
| ω | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 1,0 | |
| α | 0,016 | 0,053 | 0,115 | 0,205 | 0,320 | 0,462 | 0,646 | 0,872 | 1.192 | 1,470 | 2,025 |
Допускается также определять σ x.cr.ef по следующей формуле
| (Ш.12) |
Примечание - Коэффициент ω определяется по формуле ω = σ x /(φ0 Ry), где φ0 следует находить по таблице Ш.4 в Ш.12 при lef = l.
Для сжатой ортотропной плиты, не воспринимающей местной нагрузки, в формуле (Ш.11) коэффициент а следует принимать равным 2,025, что обеспечивает равенство расчетной длины lef продольных ребер расстоянию между поперечными ребрами l.
Ш.12 Расчет по общей устойчивости ортотропной плиты в целом (сжатой и сжато-изогнутой) при обеспечении условия (Ш.11) следует выполнять по формуле
| σ yc ≤ φ0 Rym, | (Ш.13) |
σyc - см. Ш.11
φ0 - коэффициент продольного изгиба, принимаемый по таблице Ш.4 в зависимости от гибкости λ0;
m - коэффициент условий работы, принимаемый по таблице 8.15 в 8.19. Гибкость следует определять по формуле
| (Ш.14) |
где lef - расчетная (свободная) длина продольных ребер, определяемая из выражения 
Коэффициент ω находят из таблицы Ш.3 по значению
| (Ш.15) |
а - расстояние между продольными ребрами;
th - толщина листа настила;
ξ - коэффициент, принимаемый равным 1,0 - для ортотропной плиты нижнего пояса и по таблице Ш.5 - для плиты верхнего пояса коробчатых главных балок;
А - площадь полного сечения продольного ребра;
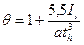- здесь It, - момент инерции полного сечения продольного ребра при чистом кручении).
Сжато-изогнутую ортотропную плиту железнодорожных мостов на общую устойчивость следует проверять по формуле (8.35), принимая гибкость по формуле (Ш.14) при ξ = 1,0.
Таблица Ш.4
| Гибкость λ0, λ1 | Коэффициент φ0 для классов прочности стали | ||
| С235 | С325 - С345 | С390 | |
| 1,00 | 1,00 | 1,00 | |
| 1,00 | 1,00 | 1,00 | |
| 1,00 | 1,00 | 0,96 | |
| 1,00 | 0,92 | 0,88 | |
| 1,00 | 0,87 | 0,83 | |
| 0,95 | 0,76 | 0,72 | |
| 0,83 | 0,64 | 0,59 | |
| 0,73 | 0,56 | 0,49 | |
| 0,64 | 0,50 | 0,43 | |
| 0,59 | 0,44 | 0,38 | |
| ПО | 0,53 | 0.39 | 0,33 |
| 0,47 | 0,34 | 0,28 | |
| 0,41 | 0,30 | 0,25 | |
| 0,36 | 0,26 | 0,22 | |
| 0,32 | 0,23 | 0,20 | |
| 0,29 | 0,21 | 0,17 | |
| 0,26 | 0,19 | 0,16 | |
| 0,23 | 0,17 | 0,14 | |
| 0,21 | 0,15 | 0,13 | |
| 0,20 | 0,14 | 0,11 |
Таблица Ш.5
| f / i | Коэффициент ξ |
| 1,00 | |
| 0,01 | 0,75 |
| 0.05 | 0,70 |
| 0,10 | 0,66 |
| Примечание - f прогиб продольного ребра между поперечными ребрами; i - радиус инерции полного сечения продольного ребра. |
Ш.13 Тавровые продольные ребра (рисунок Ш.1, в, г) сжатой ортотропной плиты нижнего пояса коробчатых главных балок при изгибно-крутильной форме потери устойчивости следует рассчитывать по формуле (Ш.13), принимая коэффициент продольного изгиба φ0 в зависимости от гибкости λ1.
Гибкость λ1 следует определять по формуле
| (Ш.16) |
где Ip = Iy + Iz + A (hw - e)2
l - см. Ш.3;
hw - высота стенки ребра толщиной tw (рисунок Ш.1, г);
е - расстояние от центра тяжести полки шириной bf, толщиной tf до центра тяжести таврового продольного ребра (рисунок Ш.1, г);
Iy, Iz - соответственно момент инерции сечения таврового продольного ребра относительно горизонтальной оси у и вертикальной оси z;
| (Ш.17) |
| (Ш.18) |
| A = bftf + hwtw; | (Ш.19) |
Для обеспечения местной устойчивости элементов таврового сечения продольного ребра толщина полки и стенки должна удовлетворять требованиям 8.45:
при bf > 0,3 hf продольное ребро полного сечения следует считать двутавром;
при bf = 0 продольное ребро полного сечения следует считать тавром;
при 0 < bf ≤ 0,3 hw требования к толщине стенки определяются по линейной интерполяции между нормами для двутавра и тавра (bf = 0).
Приложение Щ
(обязательное)
