Опытами установлено, что переход от ламинарного движения к турбулентному происходит внезапно, скачкообразно, при определенном значении безразмерного параметра. Данный безразмерный параметр получил название числа Рейнольдса:
 ,
| (2.1) |
где u - средняя скорость потока, м/с;
d - диаметр трубы, м;
n - кинематическая вязкость жидкости, м2/с.
Для каждой конкретной установки существует некоторый диапазон значений числа Re, которые можно рассматривать как критические значения Reкр, при которых и происходит смена режимов движения. На значение критического числа Рейнольдса существенное влияние оказывают различные возмущения, возникающие в потоке вследствие особенностей структуры течения до входа в трубу и при входе (сужение потока и т.п.).
Необходимо иметь в виду, что переход ламинарного движения к турбулентному удается задержать до достижения весьма больших значений Re, в то время как восстановление ламинарного движения при переходе к нему от турбулентного осуществляется при относительно малых значениях Re. В практике гидравлических расчетов именно это малое значение Re и принимают за Reкр.
При движении жидкости в круглых трубах обычно принимают Reкр = 2320. Таким образом, при Re < Reкр в потоке сохраняется ламинарный режим, а при Re > Reкр - турбулентный. Переход ламинарного режима в турбулентный происходит при увеличении скорости потока (расхода), а также при уменьшении вязкости жидкости и поперечных размеров потока (при постоянном расходе).
Если в начале и конце трубы установить пьезометры, то разность пьезометрических напоров h1 в начале и h2 в конце трубы покажет величину потери напора на трение hl при движении на расстояние l между сечениями 1-1 и 2-2 (рис. 4).
    |
|
Зависимость гидравлических потерь на трение от скорости потока имеет вид:
| (2.2) |
где a - коэффициент пропорциональности;
n - показатель степени.
При ламинарном режиме потери на трение пропорциональны средней скорости потока (n=1). При турбулентном режиме с увеличением числа Рейнольдса показатель степени в формуле (2.2) возрастает от n=1,75 до n=2. Нижний предел этого интервала соответствует области сопротивления гидравлически гладких труб, верхний предел - квадратичному закону сопротивления (гидравлически шероховатым трубам). Промежуточные значения характеризуют переходную область сопротивления.
Проведение опыта:
Для исследования и визуализации режимов течения на вход прямого трубопровода Т1 подается тонкая струйка подкрашенной чернилами жидкости, которая поступает из специальной емкости (бака) Б3. Данная лабораторная работа выполняется только при условии подключения к крану КР8 автономного источника чистой воды (например, водопровода), а также обеспечении слива с выхода крана КР12 в канализацию. Кран КР8 перед работой должен быть закрыт.
1. Полностью закрыть задвижки З1, З2, З4, З5, З6, З7, З8 и краны КР4, КР5, КР7, КР11. Краны КР10, КР12, КР14 полностью открыть.
2. Открыть кран КР8 и дождаться наполнения напорной секции накопительного бака Н2 вплоть до возникновения перелива.
3. Открыть З1 на один оборот до возникновения минимального течения через трубопровод Т1.
4. Частично закрывая кран КР14 добиться минимальной величины перелива из рабочей полости бака, для минимизации начальных возмущений.
5. Частично открыть задвижку З8 вплоть до начала истечения красящей жидкости.
6. При необходимости уменьшать расход через трубопровод, прикрывая задвижку З1, вплоть до возникновения прямой струйки окрашенной жидкости. Отрегулировать подачу красящей жидкости (З8) и минимальный перелив (КР14).
7. Закрыть кран КР10. Измерить время ∆t заполнения объема V жидкости, поступающей в мерную емкость ЕМ2. Записать значения в таблицу 2.1. Открыть кран КР10.
8. Записать режим течения жидкости, определенный визуально в таблицу 2.1.
9. Приоткрыть задвижку З1 и повторить действия, описанные в пунктах 6, 7 и 8. Результаты занести в табл. 2.1.
10. Повторять действия по пунктам 6, 7, 8 и 9 вплоть до полного открытия З1.
11. Закрыть задвижку З8.
12. Закрыть задвижку З1.
13. Выключить питание насоса Н3.
Примечание. При проведении опытов следует избегать возмущений, вызванных внешними воздействиями на установку (сотрясением и т.п.), т.е. не прикасаться к установке без необходимости, и все регулировки производить плавно.
Обработка результатов опыта:
1. Вычислить кинематическую вязкость воды по эмпирической формуле Пуазейля:
| ν = 0,179 · 10-2/ (1000 + 34Т +0,22Т2) | (2.3) |
где ν - кинематический коэффициент вязкости, м2/с;
Т – температура окружающей среды, °С.
2. Определить расход воды:
 ,
| (2.4) |
3. Рассчитать среднюю скорость жидкости:
, (2.5)
где S – площадь поперечного сечения трубопровода;
d = 15 мм – диаметр трубопровода Т1.
4. Рассчитать числа Рейнольдса по формуле (2.1)
5. Определить критическое значение числа Re для данной установки.
6. Сделать и записать выводы.
Таблица 2.1
| № | V, л | ∆t, сек | Q, л/с | u, м/с | Re | Внешний вид струйки жидкости |
Лабораторная работа № 3
ИЛЛЮСТРАЦИЯ УРАВНЕНИЯ БЕРНУЛЛИ,
ДИАГРАММА НАПОРОВ
Цель работы:
Закрепление знаний по разделу "Уравнение Бернулли для потока реальной жидкости". Наблюдение за взаимным переходом потенциальной и кинетической энергии жидкости.
Задание:
По опытным данным построить линии гидростатического напора, гидродинамического напора для элементарной струйки жидкости и гидродинамического напора для потока жидкости в наклонном трубопроводе переменного сечения.
Теоретические основы метода:
Уравнение Бернулли играет важнейшую роль в гидравлике. Оно необходимо для решения целого ряда практических инженерных задач.
Для элементарной струйки вязкой несжимаемой жидкости при установившемся движении уравнение Бернулли имеет вид:
| (3.1) |
где Z1 – высота расположения центра тяжести поперечного сечения струйки 1-1;
Z2 – высота расположения центра тяжести поперечного сечения струйки 2-2;
P1 – давление в центре тяжести сечения 1-1;
P2 – давление в центре тяжести сечения 2-2;
u1 – скорость течения жидкости в сечение 1-1;
u2 – скорость течения жидкости в сечение 2-2;
ρ – плотность жидкости;
h1,2 – потеря напора при перемещении жидкости из сечения 1-1 в сечение 2-2.
Величина 
называется полным гидравлическим напором струйки в соответствующем сечении.
Слагаемые напора:
- геометрическая высота или геометрический напор;
- пьезометрическая высота или пьезометрический напор;
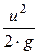- скоростная высота или скоростной напор;
- гидростатический напор.
Для потока вязкой несжимаемой жидкости уравнение Бернулли записывается в виде:
| (3.2) |
где υ1 – средняя скорость потока жидкости в сечении 1-1;
υ2 – средняя скорость потока жидкости в сечении 2-2;
α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в живом сечении. Его величина зависит от формы эпюры скорости и всегда больше единицы. Для ламинарного течения в круглых трубах α = 2, для турбулентного течения коэффициент Кориолиса обычно принимает значение в пределах α = 1,05 - 1,1.
Для определения средней скорости потока υ в сечении необходимо использовать одно из основных уравнений гидродинамики - уравнение неразрывности (постоянство объемного расхода вдоль потока несжимаемой жидкости):
| (3.3) |
где S1, S2 – площади сечений потока.
Из уравнений (3.1) и (3.2) следует, что все члены уравнения Бернулли имеют линейную размерность. Однако им можно придать и энергетический смысл.
Действительно, если масса жидкости m поднята на высоту Z над некоторой плоскостью (плоскостью сравнения), то в поле силы тяжести она обладает потенциальной энергией положения тgZ. Отнеся эту энергию к весу жидкости, найдем, что величина Z представляет собой удельную потенциальную энергию положения. – удельная потенциальная энергия давления жидкости, так как частица жидкости массой m при давлении P обладает способностью подняться на высоту и приобрести энергию положения тg (если отнести эту величину к весу жидкости тg, то получим ); 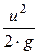– удельная кинетическая энергия жидкости. Следовательно, полный гидродинамический напор потока 
представляет собой полную удельную механическую энергию потока жидкости в данном сечении, а величина h1-2 – уменьшение удельной механической энергии потоки на участке между сечениями 1-1 и 2-2, происходящее в результате работы сил вязкостного трения, сопровождающейся необратимым переходом части механической энергии в тепловую. Таким образом, энергетический смысл уравнения Бернулли для потока (струйки) реальной жидкости заключается в том, что оно является уравнением сохранения энергии с учетом потерь. Если на участке потока уменьшается скорость (кинетическая энергия), то, согласно уравнению Бернулли, на этом участке должно соответственно возрасти давление (потенциальная энергия).
Проведение опыта:
Сложный трубопровод состоит из трех последовательно соединенных прозрачных труб из органического стекла с внутренними диаметрами dI = 15 мм, dII = 11 мм, dIII = 15 мм. Расстояния между точками отбора и схему подключения пьезометров см. рис. 1.
Для исследования влияния изменений геометрического напора конструкцией стенда предусмотрена возможность изменения угла наклона оси трубопровода к горизонту.
Переходы между участками трубопровода выполнены в виде конусов (конфузора и диффузора).
1. Полностью закрыть задвижки З1, З2, З4, З5, З6, З7, З8 и краны КР4, КР5, КР8, КР12. Краны КР6, КР7, КР9, КР14 полностью открыть.
2. Повернуть переключатель насоса НЗ в крайнее правое положение и включить питание переключением соответствующего тумблера на блоке управления.
3. Дождаться наполнения напорной секции накопительного бака, вплоть до возникновения перелива.
4. Откручивая рукоятку задвижки З6 установить уровень жидкости в пьезометре №12 (НП12) в соответствии с табл. 3.1.
5. Закрыть кран КР9. Измерить время Δt заполнения объема V жидкости, поступающей в мерную емкость ЕМ1. Записать значения в таблицу 3.1. Открыть кран КР9.
6. Записать в таблицу 3.1. показания пьезометров №13, 14, 15, 16, 17 (НП13,НП14, НП15, НП16, НП17).
7. Повторить действия, описанные в пунктах 4, 5 и 6 для всего интервала НП12 из табл. 3.1. Результаты замеров записать в табл. 3.1.
8. Изменяя угол наклона трубопровода ТЗ (контролируется по специальной линейке, размещенной на кронштейне трубопровода) при неизменной величине перекрытия задвижки З6 (рекомендуется перекрытие около 5 оборотов рукоятки задвижки), повторить измерения до пункта 8. Результаты записать в таблицу 3.2. Чтобы изменить угол наклона трубопровода ТЗ следует ослабить барашек винтового фиксатора, расположенный на тыльной стороне пластины кронштейна, придерживая поворотный механизм за металлическую прямоугольную трубу, к которой крепится прозрачный трубопровод.
9. Полностью закрыть задвижку З6.
10. Выключить питание насоса.
Обработка результатов опыта:
1. Рассчитать величину подачи 
насоса и записать значения в
таблицу 3.1.
2. Рассчитать потери статического напора по длине участков трубопровода 
; 
; 
.
3. Рассчитать местные потери пьезометрического напора:
а) В плавном сужении русла (конфузоре) 
;
б) В плавном расширении (диффузоре) 
4. Рассчитать средние скорости жидкости и критерии Рейнольдса для каждого участка по формулам:
, 
, 
,
где SI, SII – площади сечений соответствующих участков трубопровода;
ν – кинематическая вязкость жидкости (для воды при нормальных условиях ν = 10-6 м2/с = 12 мм2/с).
5. Определить коэффициенты Кориолиса, используя число Рейнольдса и данные в теоретической части лабораторной работы.
6. Рассчитать скоростные напоры на каждом участке трубопровода:
, 
, 
.
7. Рассчитать суммарные пьезометрические напоры для каждого участка:
,
,
.
Потребный пьезометрический напор сложного трубопровода:
.
8. Рассчитать потребные полные напоры участков и трубопровода в целом.
,
,
.
Полный напор сложного трубопровода с последовательным соединением:
.
9. Построить характеристики для участков трубопровода 
, 
, 
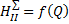, общую характеристику сложного трубопровода с последовательным соединением участков в координатах подача - потребный напор 
10. При одном фиксированном значении расхода через трубопровод (рекомендуется при максимальном) построить линии пьезометрического напора, дополнив его линиями скоростных напоров, и получить линию полного напора. Линию пьезометрических напоров следует строить по показаниям пьезометров. Линия полного напора получается при увеличении линии пьезометрического напора на величину скоростного напора.
Схематичный пример построения пьезометрической и напорной линий показан на рис. 5.
11. Сделать и записать выводы.
Рис. 5. Пьезометрическая и напорная линии.
Таблица 3.1
| № | V, л. | Δt, сек. | Q, л/с. | НП12, мм. | НП13, мм. | НП14, мм. | НП15, мм. | НП16, мм. | НП17, мм. | υI, мм/с. | υII, мм/с. | υIII, мм/с. | ReI | ReII | ReIII |
Таблица 3.1 (продолжение)
| № | ΔhI, мм. | ΔhII, мм. | ΔhIII, мм. | Δh1314, мм. | Δh1516, мм. | Δh910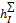, мм. |  , мм.
|  , мм.
|  , мм.
|  , мм.
|  , мм.
|  , мм.
|  , мм.
|  , мм.
|  , мм.
|  , мм.
|
Таблица 3. 2
| № | Угол наклона к горизонту ТЗ | V, л. | Δt, сек. | Q л/с. | НП12, мм. | НП13, мм. | НП14, мм. | НП15, мм. | НП16, мм. | НП17, мм. |
| -1 | ||||||||||
| -3 |
Лабораторная работа № 4
Исследование характеристик трубопроводов при различных режимах течения
Цель работы:
Закрепление знаний по разделам "Ламинарное и турбулентное течение в круглых трубах", получение навыков экспериментального определения характеристик трубопровода.
Задание:
Определить из опыта коэффициент гидравлического трения λ при заданном расходе в имеющемся трубопроводе. Сравнить полученную величину λ с величиной, определенной по справочным данным.
Теоретические основы метода:
Потери напора h на участке трубопровода в общем случае определяются из уравнения Бернулли:
| (4.1) |
