Тема 6.1. Основные понятия комбинаторики
В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения и сочетания.
Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.
Перестановки обозначаются символом Pn, где n -число элементов, входящих в каждую перестановку.
Число перестановок можно вычислить по формуле: Pn = n!
(n! – n-факториал – произведение всех натуральных чисел от 1 до n включительно)
Например: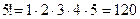 
Комбинации из m элементов по n элементов, которые отличаются друг от друга или самими элементами или порядком элементов, называются размещениями.
Размещения обозначаются символом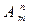 
, где m- число всех имеющихся элементов, n- число элементов в каждой комбинации. При этом полагают, что 
Число размещений можно вычислить по формуле: 
Тема 6.2. Основные понятия теории вероятности
В жизни часто встречаются явления, исход которых невозможно предсказать, результат которых зависит от случая. Случайное явление можно охарактеризовать отношением числа его наступлений к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить ли не наступить.
Теория вероятности есть раздел математики, в котором изучаются случайные явления и выявляются закономерности при массовом их повторении.
Всякое действие, явление, наблюдение с несколькими исходами, реализуемое при данном комплексе условий, называется испытанием. Результат этого испытания – случайное событие. Какое-либо определенное событие из всех возможных событий называется искомым событием. События принято обозначать: A, B, C, D…
События называются несовместными, если никакие два из них не могут наступить одновременно. В противном случае события называются совместными. Событие называется достоверным, если оно происходит в данном испытании обязательно, невозможным - не может произойти.
Пусть имеется 100 деталей, из которых 97 стандартных и 3 бракованных. Очевидно, что если взять одну деталь, то событие А, состоящее в том что эта деталь стандартная, и событие В, состоящее в том, что эта деталь бракованная, не равновозможны. Событие А более возможно, более вероятно, чем событие В.
Число, являющееся выражением меры объективной возможности наступления события, называется вероятностью этого события и обозначается символом Р(А).
Вероятность события А равна отношению числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов, т.е. Р(А)= 
.
Свойства:
1.Вероятность любого события есть неотрицательное число, не превосходящее единицы.
2.Вероятность достоверного события равна единице.
3.Вероятность невозможного события равна нулю.
Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.
Теорема сложения вероятностей: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Пример. Имеется 100 лотерейных билетов. Известно, что 5 билетов выигрышем 20 рублей,10 билетов- по 15 рублей, 15 билетов- по 10 рублей, 25 билетов- по по 2 рубля, и остальные билеты невыигрышные. Найти вероятность того, что купленный билет будет выигрышем не меньше 10 рублей.
Р е ш е н и е: Пусть А, В, С – события, состоящие в том, что на купленный билет падает выигрыш. Равный соответственно 20, 15 и 10 рублей. Т.к. А, В, С несовместные события, то Р(А+В+С)= Р(А)+Р(В)+Р(С) = 
Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет.
Событие А называется независимым от события В, если наступление события В, не оказывает ни какого влияния на вероятность наступления события А.
Теорема умножения вероятностей: Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий.
Пример. В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми»?
Р е ш е н и е: Пусть А- из первой урны извлечен белый шар, В- из второй урны извлечен белый шар. Очевидно, что оба события независимы.
Тогда Р(АВ)=Р(А) Р(В)= 
Рекомендуемая литература
- Баврин И.И. Высшая математика: Учебник. для студентов.- М.: Издательский центр «Академия», 2005.-616с
- Барахин В.Б.Введение в численный анализ: Учебное пособие.- СПб.: Издательство «Лань», 2005.-112с.
- Богатов Д.Ф. Конспект лекций и практикум по математике для юристов: Учебное пособие.- М.:«Приор-издат»,2003.-448с.
- Волков Е.А. Численные методы: Учебное пособие.- СПб.: Издательство «Лань»,2004.-256с.
- Колягин Ю.М. Математика: Учебник для ССУЗОВ.- М.: ООО «Издательство Новая Волна», 2004.-656с.
- Лунгу К.Н. Сборник задач по высшей математике: учебное пособие.- М.: Айрис-пресс,2004.-576с.
- Меняйлов А.И. Математический практикум: Учебное пособие.- М.: Академический Проект,2003.-192с.
- Омельченко В.П.Математика: Учебное пособие.- Ростов н/Д.:Феникс,2005.-380с.
- Писменный Д.Т. Конспект лекций по высшей математике. 1 часть.- М.: Айрис-пресс,2004.-288с
- Соловейчик И.Л. Сборник задач по математике для техникумов: Учебное пособие.- М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2003.-464с.
- Филимонова Е.В. Математика: Учебное пособие.- Ростов н/Д.: Феникс, 2005.-416с.
- Шипачев В.С. Задачник по высшей математике: Учебное пособие.- М.: Высшая школа, 2003.-304с.
