Множество – первичное понятие в математике, поэтому неопределяемое через другие. Математическое понятие множество постепенно выделилось из привычных интуитивных представлений о совокупности, наборе, собрании, коллекции, классе, семействе и т.д.
Георг Кантор, создатель теории множеств, дает такое пояснительное определение множества (в строгом смысле не являющееся определением): «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью», а так же «Множество есть многое, мыслимое нами как целое». Заметим, что определение Кантора с самого начала исключает из рассмотрения в математике множеств, объекты которых плохо «определены»; так, нельзя говорить о множестве идей (в прошлом или в будущем); кроме того, в определении требуется, чтобы объекты были различны между собой, т.е. множество не может содержать одинаковые элементы.
Элементами множества могут быть объекты различной природы: числа, буквы, точки, углы, предметы, люди и т.п. Множество, состоящее из конечного числа элементов, называются конечными, а множества, состоящие из бесконечного числа элементов, - бесконечными.
Бесконечные множества разделяются на счетные и не счетные. Если элементы бесконечного множества можно пронумеровать с помощью натурального ряда чисел, т.е. установить хотя бы одним способом взаимно однозначное соответствие между измеряемым множеством и эталоном – множеством натуральных чисел, то оно называется счетным. Множество действительных чисел – несчетное множество.
Конечные и счетные множества называются дискретными множествами.
Объекты, сущности или элементы, составляющие множество, обычно обозначаются строчными латинскими буквами x,y,a …; сами множества – прописными латинскими X, Y, A … Будем для выбора любого элемента множества использовать квантор всеобщности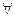 
и квантор существования 
. Множество задают либо перечислением его элементов, например 
, либо описание характеристического свойства множества 
, которое четко определяет совокупность его элементов, например 
.
Замечание. Границы множеств не всегда можно точно определить. Такие множества получили название размытых, или нечетких множеств.
Вместе с термином множество вводится (также не определяемый) термин принадлежит (синоним: «лежит в»). Если объект а принадлежит множеству А (объект а является элементом множества А), то это записывается так: 
, если же а не является элементом множества А, то записывают 
.
Запись 
– множеству А содержится в В – означает, что каждый элемент множества А принадлежит множеству В. В этом случае множество А называют подмножеством В.
Множества называют равными (А=В), если выполнено два условия: 
Множество, не содержащие ни одного элемента, называется пустым и обозначается Ø. Пустое множество считается конечным множеством. Оно является подмножеством любого множества.
Любое множество А есть подмножество самого себя. Такое подмножество называется не собственным подмножеством. К числу несобственных подмножеств принадлежит также пустое множество. Все другие подмножества исходного множества А называются собственными подмножествами.
Число подмножеств любого конечного множества, содержащего n элементов, равно 2n.
При решении определенной проблемы мы исходим из некоторого множества, элементами которого могут быть, например, различные варианты решений или
совокупность исходных данных и т.д. Множество всех элементов, которые могут встретиться в данном исследовании, называется универсальным и обозначается U.
Операции над множествами
Объединением двух множеств А и В (обозначается А 
В) называется множество С, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множества А и В, т.е. элементы множества С принадлежат или множеству А, или множеству В, или им обоим вместе:
Пересечением множеств А и В (обозначается А 
В) называется множество D, состоящие из всех тех и только тех элементов, которые принадлежат и А, и В:
Дополнением (доU) множества А (обозначается 
) называется множество всех тех элементов множества U, которые не принадлежат множеству А.
Операции объединения, пересечения и операцию дополнения { 
} часто называют булевыми операциями над множествами.
Разностью множеств А и В (обозначается А\В) называется множество G всех тех и только тех элементов А, которые не содержатся в В:
Введенная операция разности А\В двух множеств выражается через операции пересечения и дополнения следующим образом:
Декартовым произведением множеств А и В (обозначается А×В) называется множество F всех упорядоченных пар (aibi), где 
т.е. 
Декартово произведение множеств является важнейшей операцией над множествами, поскольку на основе её строится важнейшая категория в математики – функция, математическая модель процессов в окружающем нас мире.
Симметрической разностью множеств А и В (обозначается А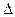 
В) называется множество М, которое определяется как объединение разностей А\В и В\А:
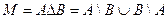
Введенные операции позволяют выражать одни множества через другие. Порядок выполнения операций следующий с начало выполняется операция дополнения, затем пересечения и только затем операция объединения (разности). Для изменения этого порядка в выражениях необходимо использовать скобки.
Способ задания множества выражением, в которое входят идентификаторы (обозначения) множеств, введенные выше операции и, быть может, скобки, называется аналитическим.
