Задание 1
В задачах 1-20 решить систему уравнений методами Крамера, Гаусса, записать ее в матричной форме и решить с помощью обратной матрицы.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Задание 2
В задачах 1-20 даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А; 4) уравнения высоты СD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник ABC.
1. A (0;-1), B(12;8), C(10;-6). 2. A (-7; 2), B(5; 11), C(3; -3).
3. A (-5;-3), B(7;6), C(5;-8). 4. A (-6;-2), B(6;7), C(4;-7).
5. A (-3;3), B(9;-6), C(7;8). 6. А (-5; 0), B(7; 9), C(5; -5).
7. A (-6;11), B(6;10), C(4;-4). 8. A (-2;-4), B(10;5), C(8;-9).
9. A (-3;0), B(9;9), C(7;-5). 10. A (-9;2), B(3;7), C(1;-7).
11. A (-5;2), B(7;-7), C(5;7). 12. A (-7;5), B(5;-4), C(3;10).
13. A (-7;1), B(5;-8), C(3;6). 14. A (0;3), B(12;-6), C(10;8).
55. A (-8;4), B(4;-5), C(2;9). 16. A (-2;2), B(10;-7), C(8;7).
17. A (1;2), B(13;-7), C(11;7). 18. A (-4;1), B(8;-8), C(6;6).
19. A (-7;-1), B(-5;-10), C(3;4). 20. A (-8;-4), B(4;5), C(2;-9).
Задание 3
В задачах 1-10 составить уравнение линии, для каждой точки которой отношение расстояний до точки А (х1; у1) и до прямой х = а равно числу e. Полученное уравнение привести к простейшему виду и построить кривую.
1. A(4;0), a = 9, ε = 
. 2. A(-8;0), a = - 2, ε =2.
3. A(4;0), a = 1, ε = 2. 4. A(9;0), a = 4, ε = 1.5.
5. A(-1;0), a = -4, ε = 
. 6. A(5;0), a =9, ε = .
7. A(-1;0), a = -4, ε = 8. A(4;0), a = 7, ε =
9. A(3;0),a = 8, ε = 10. A(-4;0),a = -2, ε =3.
В задачах 11-20 составить уравнение линии, для каждой точки которой ее расстояние до точки А (х1; у1) равно расстоянию до прямой у = b. Полученное уравнение привести к простейшему виду и построить кривую.
11. А (2;1), b=- 1. 12. A (-2; -2), b= - 4.
13. A (2;-1), b=2. 14. A (2; -1), b=1.
15. A (4; -1), b=1. 16. А (4;1), b=- 1.
17. А (3;1), b=- 1. 18. А (2;1), b=- 2.
19. А (4;1), b=- 2. 20. А (6;1), b=- 1.
Задание 4
В задачах 1-20 даны координаты точек А, В, С. Требуется: 1) записать векторы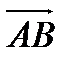 
и 
в системе орт и найти модули этих векторов; 2) найти угол между векторам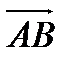и и ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору .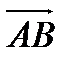
1. А(7;-4;1), B(12;-3;1), C(10;1;5). 2. А(0;-3;3), B(5;-2;3), C(3;2;7).
3. А(-2;-1;-2), B(3;0;-2), C(1;4;2). 4. А(-6;0;0), B(-1;1;0), C(-3;5;4).
5. А(-2;-3;-8), B(3;-2;-8), C(1;2;-4). 6. А(1;0;-1), B(6;1;-1), C(4;5;3).
7. А(-1;4;1), B(4;5;1), C(2;9;5). 
8. А(3;-6;-3), B(8;-5;-3), C(6;-1;1).
9. А(1;0;0), B(6;1;0), C(4;5;4). 10.А(2;-8;-2),B(7;-7;-2), C(5;-3;2).
11. А(1;-2;3), B(0;-1;2),C(3;-4;5). 12.А(0;-3;6),B(-12;-3;-3),C(-9;-3;-6).
13. А(3;3;-1), B(5;5;-2), C(4;1;1) 14. А(-1;2;-3), B(3;4;-6), C(1;1;-1).
15. А(-4;-2;0), B(-1;-2;4), C(3;-2;1). 16. А(-3;-7;-5), B(0;-1;-2), C(2;3;0).
17. А(3;3;-1), B(1;5;-2), C(4;1;1). 18. А(0;0;4), B(-3;-6;1), C(-5;-10;-1).
19. А(7;0;2), B(7;1;3), C(8;-1;2). 20. А(0;3;-6), B(9;3;6), C(12;3;7).
Задание 5
Даны координаты вершин пирамиды АВСD. Найти:
1) векторы 
в системе орт и их модули;
2) угол между векторами 
;
3) площадь грани АВС;
4) объем пирамиды АВСD;
5) уравнение ребра АВ;
6) уравнение плоскости АВС;
7) уравнение и длину высоты, опущенной из точки D на плоскость АВС.
1. А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9).
2. А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10).
3. А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10).
4. А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10).
5. А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8).
6. А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9).
7. А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9).
8. А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10).
9. А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9).
10. А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10).
11. А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10).
12. А(0;1;2), В(-2;4;2), С(-2;1;8), D(0;4;10).
13. А(0;3;0), В(-2;6;0), С(-2;3;6), D(0;6;8).
14. А(2;1;0), В(0;4;0), С(0;1;6), D(2;4;8).
15. А(0;2;1), В(-2;5;1), С(-2;2;7), D(0;5;9).
16. А(1;1;1), В(-1;4;1), С(-1;1;7), D(1;4;9).
17. А(1;2;0), В(-1;5;0), С(-1;2;6), D(1;5;8).
18. А(0;1;0), В(-2;4;0), С(-2;1;6), D(0;4;8).
19. А(0;1;1), В(-2;4;1), С(-2;1;7), D(0;5;9).
20. А(0;2;0), В(-2;5;0), С(-2;2;6), D(0;5;8).
Задание 6
В задачах 1-20 даны векторы 
, 
, 
, 
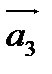. Показать, что векторы
, 
, 
образуют базис трехмерного пространства, и найти координаты вектора в этом базисе.
1. (2;1;3), (3;-2;1), (1;-3;-4), (7;0;7).
2. (5;3;1), (-2;-1;2), (-2;1;4), (3;0;1).
3. (1;3;5), (-2;-1;-1), (4;-2;4), (-7;3;-1).
4. (3;1;6), (-2;2;-3), (-4;5;-1), (3;0;1).
5. (4;1;4), (-2;-1;1), (3;1;5), (-3;-2;1).
6. (1;2;5), (2;-3;4), (1;-1;-2), (3;0;1).
7. (5;1;2), (3;4;-1), (-4;2;1), (-3;5;4).
8. (2;1;5), (-4;3;5), (1;-1;-4), (4;-1;-3).
9. (3;1;4), (-4;2;3), (2;-1;-2), (7;-1;0).
10. (1;4;2), (5;-2;-3), (-2;-1;1), (-3;2;4).
11. (2;1;3), (3;-2;1), (1;-3;-4), (7;0;7).
12. (5;3;1), (-2;-1;2), (-2;1;4), (3;0;1).
13. (1;3;5), (-2;-1;-1), (4;-2;4), (-7;3;-1).
14. (3;1;6), (-2;2;-3), (-4;5;-1), (3;0;1).
15. (4;1;4), (-2;-1;1), (3;1;5), (-3;-2;1).
16. (1;2;5), (2;-3;4), (1;-1;-2), (3;0;1).
17. (5;1;2), (3;4;-1), (-4;2;1), (-3;5;4).
18. (2;1;5), (-4;3;5), (1;-1;-4), (4;-1;-3).
19. (3;1;4), (-4;2;3), (2;-1;-2), (7;-1;0).
20. (1;4;2), (5;-2;-3), (-2;-1;1), (-3;2;4).
Литература
1 Письменный Д.Т. Конспект лекций по высшей математике (ч.1,2)./Письменный Д.Т.-М.:«Айрис-пресс»,2007.-282с., 253с.
2 Клетеник Д.В. Сборник задач по аналитической геометрии / Клетеник Д.В. -М.: Наука, 2005.
3 Лунгу К.Н. Сборник задач по высшей математике (ч.1,2) -М.: «Айрис - пресс», 2008-574с.
Дополнительная литература
1 Данко П.Е., Попов А.Г. Высшая математики в упражнениях и задачах. / Данко П.Е. Попов А.Г. и др. - М.: Высшая школа, т.1,2, 2006-304с, 416с.
2 Шипачев В.С.Задачник по высшей математике. - М.: Высшая школа, 2008.-304с.
3 Кремер Н.Ш. Высшая математика для экономистов. - М.: «Юнити», 1999.-471с.
