Пусть дана система n уравнений с n неизвестными:
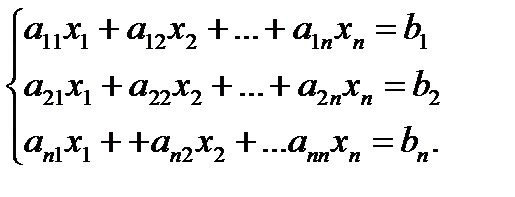
Основная матрица А такой системы квадратная. Определитель этой матрицы
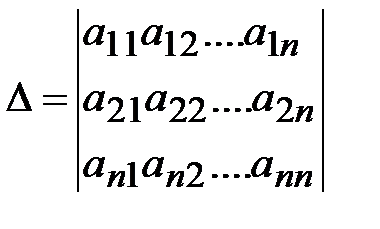
называется определителем системы.
Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.
В дальнейшем мы будем иметь дело только с такими системами.
Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.
Формулы Крамера имеют вид: 
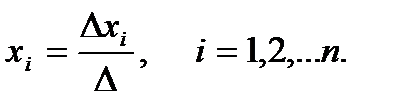
Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.
Решение осуществляется в два этапа: 1) система приводится к треугольному виду, 2) последовательно определяют неизвестные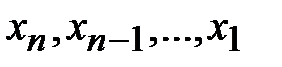 
.
Задача 1.
Решить систему уравнений методами Крамера и Гаусса:
Решение:
а) Метод Крамера.
Найдем определитель системы 
. Предварительно сложив второй столбец с третьим и разложив определитель по элементам последнего столбца.
= 
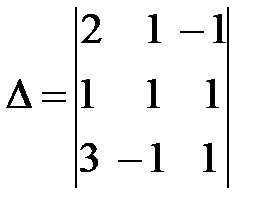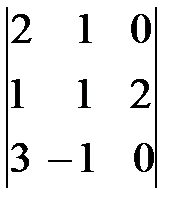=2(-1)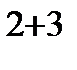 
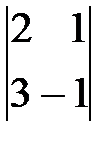=-2(-2-3)=10 
.
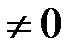Так как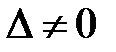 
, то система имеет единственное решение.
Найдем определител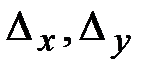и 
и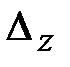 
, заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов (при вычислении определителя 
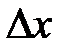выполним преобразования аналогичные предыдущим):
= 
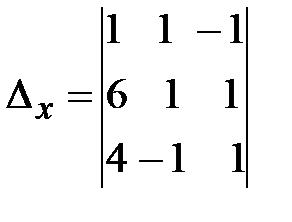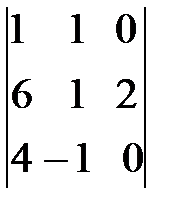=2(-1)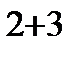 
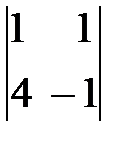-2(-1-4)=10.
При вычислении определителя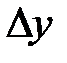 
последнюю строку складываем с первой и вычитаем из второй строки. Разлагаем по элементам последнего столбца.
= 
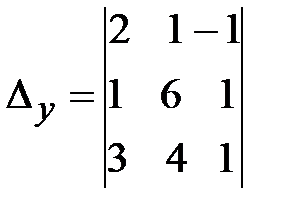=1(-1)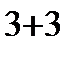 
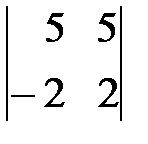=10+10=20.
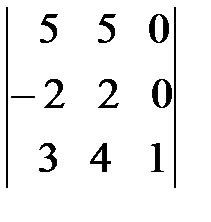
При вычислении определителя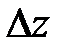 
последнюю строку складываем с первой и со второй строки и разлагаем получившийся определитель по элементам второго столбца.
= 
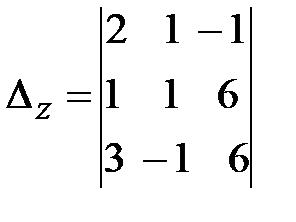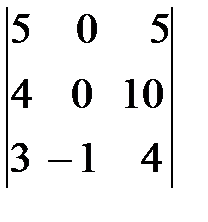=-1(-1)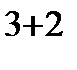 
=50-20=30.
Подставляя найденные значения в формулы Крамера получим:
x =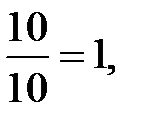 
у = 
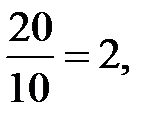z =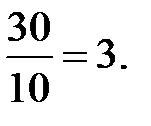 
б) Метод Гаусса.
Составим расширенную матрицу системы:
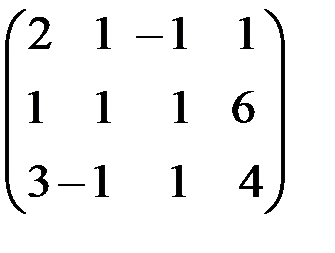
Разрешающим элементом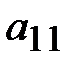 
удобно иметь единицу, поэтому переставим второе уравнение на место первого.
Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.
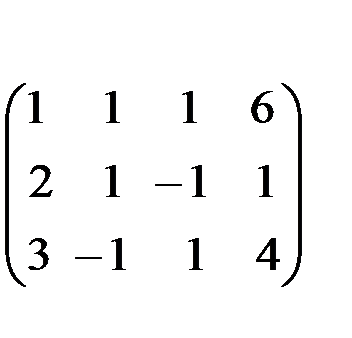(-2) (-3) 
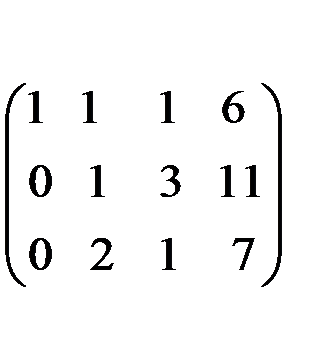
С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.
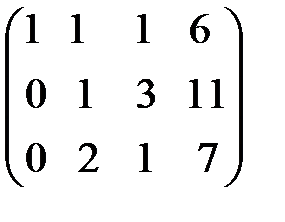(-2)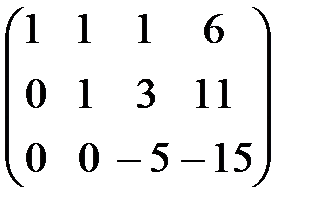 
.
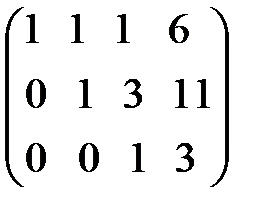Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:
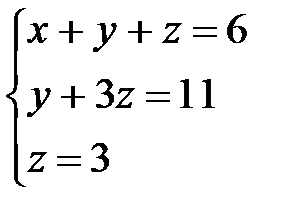
Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у = 11-3z = 11-9 = 2. Затем из первого уравнения найдем
х = 1, у = 2, z = 3.
Разберите решение задачи 5 данного пособия.
Задача 5. Данную систему уравнений записать в матричной форме и решить ее c помощью обратной матрицы:
x1— 2х2+x3=1
2x1+3х2 — x3=8
x1 — х2+2х3= -1 
Решение. Обозначим через А матрицу коэффициентов при неизвестных; Х — матрицу-столбец неизвестных Х1, X2, X3; H - матрицу-столбец свободных членов:
1 -2 1 X1 1
А= 2 3 -1, Х= Х2, H= 8.
1 -1 2 X3 -1
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: A× Х=Н (l)
Если матрица А — невырожденная (ее определитель 
отличен от нуля), то она имеет обратную матрицу А-1. Умножив обе части уравнения (1) на А-1 слева получим:
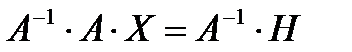
Но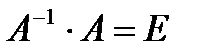 
(Е — единичная матрица), а ЕХ=Х, Поэтому
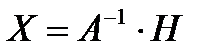(2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Пусть имеем невырожденную матрицу
а11 а12 а13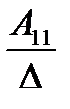 
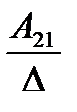
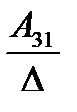
А= а21 а22 а23. Тогда А-1 =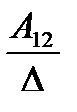 
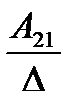
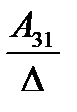
а31 а32 а33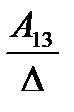 
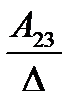
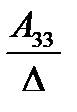
где Аij (i=1, 2, 3; j=l, 2, 3) — алгебраическое дополнение элемента аij в определителе матрицы А, которое является произведением (-l)i+j на минор (определитель) второго порядка, полученный вычерчиванием i-й строки и j-гo столбца в определителе матрицы А.
Вычислим определитель и алгебраические дополнения Аij элементов матрицы А.
1 -2 1
= 2 3 -1 =10 
0, следовательно, матрица А имеет обратную матрицу А-1
1 -1 2
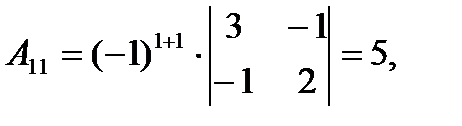
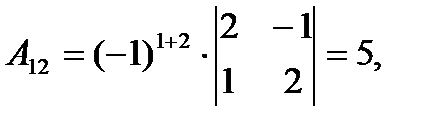
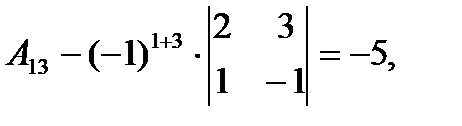
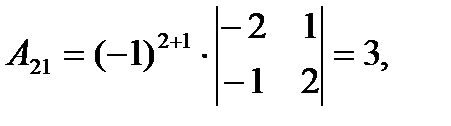
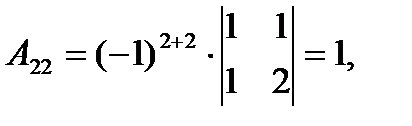
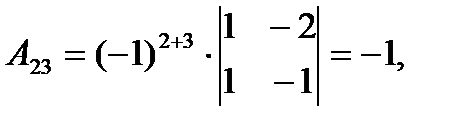
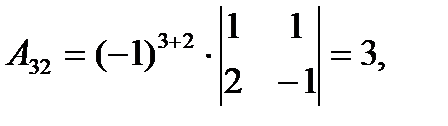
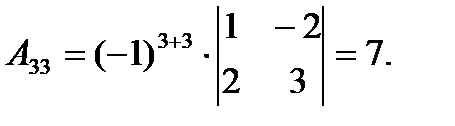
Тогда
5 3 -1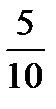 
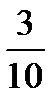
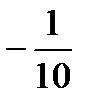
А-1=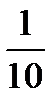 
-5 1 3 =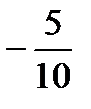 
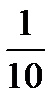
-5 -1 7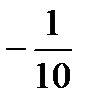 
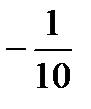
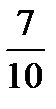
По формуле (2) находим решение данной системы уравнений в матричной форме:
= 
×
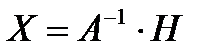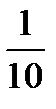
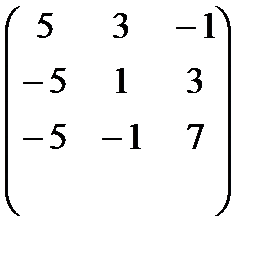Таким образом, Х = (3; 0; -2).
Вопросы для самопроверки
1. Что называется определителем второго, третьего, n-го порядков?
2. Назовите основные свойства определителей.
3. Что называется минором, алгебраическим дополнением элемента определителя?
4. Напишите формулы Крамера решения системы линейных уравнений. В каких случаях их можно использовать?
5. Назовите схему решения системы линейных уравнений по методу Гаусса.
6. Что называется матрицей?
7. Как определяются основные действия над матрицами?
8. Какая матрица называется обратной по отношению к данной матрице? Как найти матрицу, обратную данной?
9. Что называется рангом матрицы? Как найти ранг матрицы?
10. Сформулируйте теорему Кронекера - Капелли.
11. Опишите матричный способ решения системы линейных уравнений.
12. Какова геометрическая интерпретация систем линейных уравнений и неравенств?
