Нетрудно показать, что введенные выше линейные операции обладают свойствами:
1) 
2) 
3) 
+ (– ) =`0
4) +0 =
5) 1 =
6) (a + b) = a + b
7) (ab) = a(b )
8) a( + 
) = a + a
Итак, на множестве геометрических векторов (множестве векторов прямой, плоскости, или пространства) определены две операции – сложения и умножения на число, которые называют линейными операциями, и эти операции обладают рядом свойств.
Можно привести примеры и других множеств (множество действительных чисел, множество комплексных чисел, множество матриц одинаковой размерности и т.д.), на которых также введены линейные операции. И хотя эти операции на каждом множестве определяются по-своему, свойства этих операций совпадают со свойствами 1) – 6) линейных операций над геометрическими векторами. Поэтому естественно возникает потребность изучать множества элементов произвольной природы, на которых определены линейные операции. Причем операции могут быть заданы каким угодно способом, лишь бы обладали определенным набором свойств. Такие множества в математике называют линейными пространствами. Основные положения теории линейных пространств играют важную роль при изучении многих разделов математики, механики, физики.
Таким образом, множество свободных геометрических векторов образует линейное пространство. Пространство векторов плоскости обозначают V2, множество векторов трехмерного пространства обозначают V3. Пространство векторов, расположенных на одной прямой (или параллельных одной прямой) обозначают V1.
Доказано, что во всяком линейном пространстве существует такая совокупность элементов { а 1, а 2, …, а п }, что любой элемент х пространства единственным образом представим в виде суммы элементов этой совокупности, взятых с некоторыми числовыми коэффициентами
(в этом случае говорят: «х представлен в виде линейной комбинации векторов а 1, а 2, …, а п»). Такая совокупность элементов называется базисом линейного пространства, а количество элементов в этой совокупности –размерностью пространства.
Справедлива теорема:
Теорема 2.
Базис пространства V1 образует любой ненулевой вектор.
Базис пространства V2 образуют любые два неколлинеарных вектора.
Базис пространства V3 составляют любые три некомпланарных вектора.
Доказательство: Как сказано выше, если совокупность 
1, 2, …, k. векторов линейного пространства является базисом, то " вектора выполняется равенство
= b1 1+ b2 2 + …+ b k k,
где b i – некоторые числа.
1) Рассмотрим произвольный ненулевой вектор Î V1. Так как все векторы V1 лежат на одной прямой, то они коллинеарны, следовательно, для любого вектора ` а Î V1 можно записать 
, значит, вектор образует базис в V1.
2) Рассмотрим два произвольных неколлинеарных вектора ` а и` b Î V2. Покажем, что "` с Î V2 $ х, у Î R2, такие, что 
.
Рассмотрим произвольный вектор ` с Î V2, пусть, например, 
(рис. 6). Через точку С проведем прямую, параллельную вектору ` b, а через точку D – прямую, параллельную вектору` а. Тогда вектор 
параллелен вектору ` а и значит, = х , а вектор 
параллелен вектору и = у . Следовательно, из треугольника, получаем
= 
,
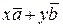что и требовалось доказать.
Утверждение 3) доказать самостоятельно.
Равенство называется разложением вектора ` с по базису {` a,` b }, коэффициенты х и у этого разложения называются координатами вектора` с в базисе {` a,` b }, запись ` с = (х, у) называется координатной формой вектора ` с.
Если ` a,` b, ` с – некомпланарные векторы, то они образуют базис пространства V3, поэтому "` d Î V3 разложение по базису {` a,` b, ` с } имеет вид
,
а в координатной форме `d = (x, y, z).
Совокупности чисел (х, у) или (x, y, z) представляют собой, по сути, матрицы-строки длины 2 и 3 соответственно*). Поэтому операции над векторами в координатной форме выполняются по правилам действий над матрицами.
Например,если два вектора и пространства V3 заданы своими координатами = (аx, ay, az) и = (bx, by, bz), то
= Û ax = bx, ay = by, az = bz;
± = (аx ± bx, ay ± by, az ± bz);
a = (a аx, a ay, a az).
Если векторы = (аx, ay, az) и = (bx, by, bz), коллинеарны, то выполняется равенство , откуда (аx, ay, az) = (l bx, l by, l bz), или
ax = l bx, ay = l by, az = l bz,
.
Значит, если векторы коллинеарны, то их координаты пропорциональны.
Наоборот, если координаты двух векторов пропорциональны, то имеем:
Þ (аx, ay, az) = (l bx, l by, l bz) Þ ,
а это значит, что векторы коллинеарны.
Таким образом, мы доказали: для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны.
Рассмотрим произвольную прямую l и на ней орт ` е. Этот орт порождает на прямой l семейство векторов, лежащих на этой прямой: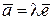 
. При l > 0 ` а 
` е, при l < 0 ` а 
` е, значит, орт` е определяет на прямой l два противоположных направления.
Прямая, на которой выбрано направление, называется осью, а орт, задающий это направление, называется ортом оси. Направление, сонаправленное с направлением орта, называется положительным, противоположное направление – отрицательным. Орт также определяет на оси масштаб и начало отсчета (точку его приложения). Проекция вектора на ость есть проекция вектора на орт оси:
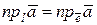
Если в пространстве V3 выбрана точка О и произвольный базис {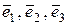 
} с началом в точке О, то четверку {O, 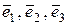} называют репером. Говорят, что в V3 задана декартова система координат (афинная система координат), если в нем задан репер и с каждым вектором репера связана ось, называемая координатной осью. Первая из этих осей, соответствующая вектору ` е 1, называется осью абсцисс, вторая – осью ординат, третья – осью аппликат. Обозначают систему координат обычно ОХУZ. Тогда каждой точке М трехмерного пространства ставится в соответствие тройка чисел М(х, у, z) – координат вектора 
(радиус-вектора этой точки) в базисе { }.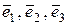
Аналогично вводится понятие системы координат на плоскости.
Обозначим ` i, ` j, ` k – взаимно перпендикулярные единичные векторы: 
, ` i ^` j ^` k. Очевидно, эти векторы образуют базис в V3. Базис 
называется о ртонормированным. Декартова система координат, порожденная репером {О,` i, ` j, ` k }, называется декартовой прямоугольной системой координат. Таким образом:
Декартовой прямоугольной системой координат в трехмерном пространстве называют совокупность
- некоторой точки О, называемой началом координат;
- ортонормированного базиса .
В дальнейшем мы будем рассматривать декартову прямоугольную систему координат (ДПСК).
В декартовой прямоугольной системе координат координаты вектора = (аx, ay, az) равны соответственно проекциям этого вектора на координатные оси: аx = 
, ay =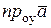 
, az = 
.
Базисные векторы ` i, ` j, ` k в ДПСК имеют координаты
` i = (1, 0, 0) ` j = (0, 1, 0) ` k = (0, 0, 1) в V3,
`i = (1, 0) ` j = (0, 1) в V2.
Рассмотрим произвольный вектор Î V3, углы, которые этот вектор образует с осями координат (или с базисными ортами ` i, ` j, ` k) обозначим a = 
, b = 
, g = 
(рис.7). Косинусы этих углов cosa, cosb, cosg называются направляющими косинусами вектора . Направляющие косинусы заданного вектора обладают свойством
cos2a + cos2b + cos2 g = 1.
Они характеризуют направление вектора относительно ДПСК.
Каждой точке М плоскости (пространства) в выбранной ДПСК можно поставить в соответствие её радиус-вектор . Координатами точки в ДПСК называют координаты её радиус-вектора.
Если известны координаты точек А(х А, у А, z A) и B((х B, у B, z B) – начала и конца вектора , то координаты этого вектора можно найти по правилу «от координат конца вектора отнять соответствующие координаты начала»:
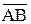= (х B – х А, у В – у А, z B – z A).
Лекция 9. Умножение векторов. Приложения
Содержание лекции: Векторное произведение векторов, геометрический и физический смысл, свойства. Смешанное произведение трех векторов, его свойства, геометрический смысл, приложения.
Скалярное произведение векторов, его свойства, приложения.
