Понятие вектора и простейшие операции над векторами вы изучали еще в школе. Вспомним кратко, что:
- 
геометрический вектор – это направленный отрезок прямой. Обозначается вектор: а, 
, 
, 
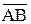, где А – начало вектора, В – конец; В математике рассматриваются только свободные векторы, т.е. векторы, начало которых выбирают произвольно.
- модулем (длиной) вектора называется длина отрезка, изображающего вектор; обозначается модуль вектора | 
|, или | |;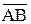
- вектор, начало и конец которого совпадают (т.е. точка), называется нулевым вектором и обозначается 
, направление вектора не определяется, длина его равна 0;
- вектор, длина которого равна единице, называется единичным вектором или ортом;
- вектор 
называется противоположным вектору 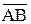, для вектора противоположный обозначается (– ).
- два вектора называются равными, если они имеют равные модули и одинаково направлены, записывают: 
.
- векторы 
и 
называют коллинеарными, если они лежат на одной или на параллельных прямых, обозначают 
. Коллинеарные векторы называют сонаправленными, если их направления совпадают, обозначают` 
; в противном случае векторы – противоположно направленные, это обозначают 
. Заметим, что;
- ортом вектора ` а называется вектор` а о такой, что 
и 
=1(рис.1);
-
|
и ;
- 
углом между векторами называется наименьший угол, на который нужно повернуть один из них, чтобы направления этих векторов совпали; обозначают угол между векторами ` а и` b символом 
;
- векторы называются ортогональными, если угол между ними равен 90о; ортогональность векторов ` а и` b обозначают ` а ^` b;
- проекцией вектора ` а на вектор ` b называется число
.
Рассмотрим операции над векторами.
Суммой векторов 
и называют вектор 
, начало которого (точка А на рисунке 1,а) совпадает с началом вектора , а конец (точка С) – с концом вектора , если конец вектора (точка В) совмещен с началом вектора . Обозначают 
Очевидно, введенная таким образом операция сложения применима для любых векторов плоскости или пространства (рисунок 2,а), в том числе и для векторов, лежащих на одной прямой (рисунок 2,б)
 |
Если дополнить треугольник АВС (рисунок 3) до параллелограмма АВСD, то легко получить известное «правило параллелограмма»: если начала неколлинеарных векторов и совмещены, то их сумма изображается вектором, имеющим начало в той же точке и совпадающим с диагональю параллелограмма, построенного на векторах и 
(рисунок 3).
Разность 
векторов` а и` b определяется равенством = + (–` b), где (
) – вектор, противоположный вектору` b.
Напомним, что в параллелограмме ОАСВ (рис.4) сумма есть вектор-диагональ 
, исходящая из общего начала О векторов и` b, а разность этих векторов есть другая вектор-диагональ – вектор, направленный из конца вычитаемого вектора к концу уменьшаемого.
Произведением вектора на число 
называется вектор a , такой, что:
1. |a | = |a|.| |;
2. векторы и a сонаправлены, если 
; векторы и a противоположно направлены, если 
(рисунок 5).
 |
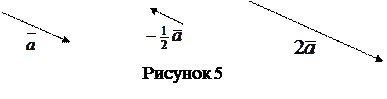Заметим, что используя определение операции умножения вектора на число, можно рассматривать вектор (– 
), противоположный вектору , как произведение 
.
Используя определение орта вектора и операцию умножения, можно для любого вектора` а записать: = | |.` а о и наоборот, ` а о = 
.
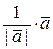Справедлива также следующая теорема:
Теорема 1.
Векторы ` а и` b коллинеарны тогда и только тогда, когда существует отличное от нуля число a такое, что = a 
.
Доказательство: 1) если = a , a ¹ 0, то, по определению произведения вектора на число, ` а и` b коллинеарны.
2) Пусть ` а и` b коллинеарны. Рассмотрим ` а о и ` b о, они, очевидно, тоже коллинеарны. Значит, либо ` а о 
` b о, либо ` а о 
` b о и |` а о| = |` b о| = 1. Но тогда либо ` а о =` b о, ` а о = –` b о, откуда =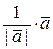 
, или 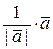= – . Следовательно, либо 
, либо 
, но это и означает, что существует a = 
такое, что = a . ЧТД.
