Движение жидкости (газа) по трубам. Формула Пуазейля.

Существует два режима течения жид­костей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относи­тельно соседних, не перемешиваясь с ни­ми, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Рейнольдс установил, что ха­рактер течения зависит от безразмерной величины, называемой числом Рейнольдса:

где — кинематическая вязкость;

r — плотность жидкости; (v)—средняя по сечению трубы скорость жидкости; d — характерный линейный размер, например диаметр трубы. При малых значениях числа Рейнольдса (Re£1000) наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области 1000£:Re£2000, а при Re = 2300 (для гладких труб) течение — турбулентное. Если число Рейнольдса одинаково, то ре­жим течения различных жидкостей (га­зов) в трубах разных сечений одинаков.

Методы определения вязкости

1. Метод Стокса. Этот метод определе­ния вязкости основан на измерении скоро­сти медленно движущихся в жидкости не­больших тел сферической формы.

Измерив скорость равномерного движения шарика, можно определить вязкость жид­кости (газа).

2. Метод Пуазейля. Этот метод осно­ван на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мыс­ленно выделим цилиндрический слой ради­усом r и толщиной dr (рис. 54).

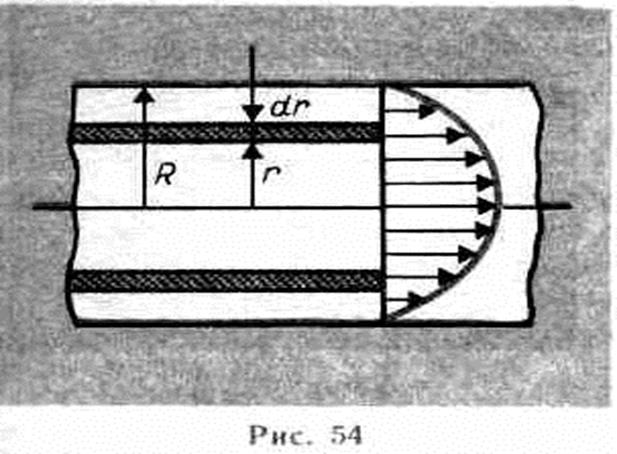
Сила внут­реннего трения, действующая на боковую поверхность этого слоя,

где dS — боковая поверхность цилиндри­ческого слоя; знак минус означает, что при возрастании радиуса скорость уменьша­ется.

Для установившегося течения жидко­сти сила внутреннего трения, действую­щая на боковую поверхность цилиндра, уравновешивается силой давления, дей­ствующей на его основание:

После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получим

Отсюда видно, что скорости частиц жид­кости распределяются по параболиче­скому закону, причем вершина параболы лежит на оси трубы. За время t из трубы вытечет жидкость, объем которой

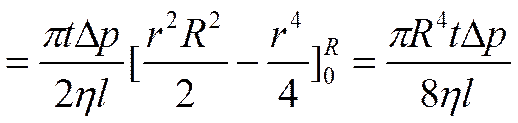
Откуда вязкость

14.
Реальные газы и жидкости.

Изотермы реального газа. Уравнение Ван-дер-Ваальса. Поверхностное натяжение. Давление Лапласа. Капиллярные явления. Осмос.

Для реальных газов необходимо учитывать размеры мо­лекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона—Менделеева.

(для моля газа), описывающее иде­альный газ, для реальных газов непри­годны.