II закон термодинамики. Тепловые двигатели.

Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана.

Закон равномерного распределения энергии по степеням свободы молекул.

 

В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/ 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее прихо­дится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциаль­ной энергий одинаковы. Таким образом, средняя энергия молекулы

где i — сумма числа поступательных, числа вращательных в удвоенного числа колеба­тельных степеней свободы молекулы:

Внутренняя энергия для произвольной массы т газа.

где М — молярная масса, n — количество вещества.

С редняя длина свободного пробега молекул и эффективный диаметр молекулы.

 

Классическое распределение по скоростям (Максвелла):

Справедливо для всех частиц:

 

dN – число частиц, попадающих в определенный интервал скоростей.

N – число всех частиц.

f(V) – функция распределения по скоростям

dV – элементарный объем скоростей.

 

Рассмотрим функцию распределения по скоростям в сферической системе координат:

 

 

- функция распределения Максвелла.

 

 

 

 

 

 

 

 

Величина А (амплитуда вероятности) находится из условия нормировки:

- условие нормировки

 

;

 

Аналогично находим j(v_y) и j(v_z):

 

 

 

тогда

 

 

 

 

 

Барометрическая формула. Распределение Больцмана.

 

 

Первое закон термодинамики.

 

Внутренняя энергия системы. Теплоемкость вещества. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам в идеальном газе. Адиабатический процесс.

 

 

 

Внутренняя энергия газа

 

Теплоемкость вещества.

 

 

 

 

 

 

 

 

 

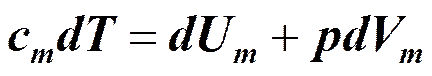
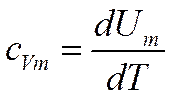
Применение первого начала термодинамики к изопроцессам.

 

Изохорный процесс (V =const).

 

 

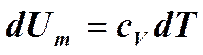
Изобарный процесс (p =const).
Для работы изобарного расширения

 

 

 

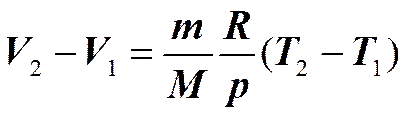
Изотермический процесс (T =const).

 

 

 

 

Адиабатический процесс.

 

 

Уравнения Пуассона:

 

 

12.

II закон термодинамики. Тепловые двигатели.

Обратимые и необратимые процессы. II закон термодинамики в формулировках Томсона и Клаузиуса. Энтропия. Статистический смысл энтропии. Теорема Нернста. Круговые процессы (циклы). Цикл Карно. КПД тепловой машины. Термодинамические T-S диаграммы. Теорема Карно.

Термодинамический процесс называет­ся обратимым, если он может происходить как в прямом, так и в обратном направле­нии, причем если такой процесс происхо­дит сначала в прямом, а затем в обратном направлении и система возвращается в ис­ходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетво­ряющий этим условиям, является необра­тимым.

Любой равновесный процесс является обратимым. Обратимые процес­сы — это идеализация реальных процес­сов.