2.2.5. * Деякий газ перебуває за температури 117 °С. Для ізобаричного нагрівання газу на 100 °С потрібно 4100 Дж теплоти. При ізохоричному охолодженні газ віддає 5040 Дж теплоти, а тиск газу зменшується в 3 рази. Визначити відношення теплоємностей за сталого тиску і сталого об'єму.
2.2.6. Для ізохоричного нагрівання 10 г газу на 10 °С потрібно 630 Дж теплоти, а для ізобаричного — 1050 Дж. Визначити молярну масу газу.
2.2.7. * Азот за тиску 0.1 МПа займає об'єм 4 л. а за тиску 0.8 МПа — 1л. Визначити кількість теплоти, надану газу в процесі переходу з І першого стану в другий, а також зміну внутрішньої енергії і виконану газом роботу, якщо процес спочатку відбувався ізохоричне, а потім — ізобаричне. Побудувати графік процесу.
2.2.8. * Кисень за тиску 0,1 МПа займає об'єм 4 л, а за тиску 0,8 МПа — 1 л. Визначити кількість теплоти, надану газу в процесі переходу з першого стану в другий, а також зміну внутрішньої енергії і виконану газом роботу, якщо процес спочатку відбувався ізобаричне, а потім — ізохоричне. Побудувати графік процесу.
2.2.9. Водень масою 10г нагріли на 100 °С. При цьому газу було надано теплоту 3,35×104 Дж. Знайти зміну внутрішньої енергії газу і виконану ним роботу.
2.2.10. * Кисень масою 1 кг займає об'єм 1 м3 і перебуває під тиском 1 атм. Газ був нагрітий спочатку за сталого тиску до об'єму 3 м3, а потім за сталого об'єму — до тиску 5 атм. Знайти зміну внутрішньої енергії газу, виконану ним роботу й отриману теплоту. Побудуйте графік процесу.
2.2.11. Теплова електростанція (ТЕЦ) потужністю 100 кВт споживає за 1 год роботи 80 кг вугілля з питомою теплотою згоряння 3,3×І07 Дж/кг. Температура котла дорівнює 400 °С, а температура холодильника — 15 °С. Визначити термічний ККД ТЕЦ і порівняти його з ККД ідеальної машини Карно, що працює за тих самих температур нагрівача і холодильника.
2.2.12. * Ідеальна холодильна машина, що працює за оборотним циклом Карно, передає теплоту від холодильника з температурою 0°С гарячому джерелу з температурою 100 °С. Визначити, яка кількість води, взятої при 0°С, перетворюється в холодильнику на лід, якщо внаслідок цього в пару, перетворюється 1 кг води при температурі гарячого джерела.
2.2.13. В оборотному циклі Карно робота ізотермічного розширення робочого тіла дорівнює 6 кДж, температура нагрівача — 150 °С, температура холодильника— 10 °С. Визначити роботу ізотермічного стискання.
2.2.14. В оборотному циклі Карно робота ізотермічного стискання робочого тіла дорівнює 700 Дж, температура нагрівання — 400°С, температура холодильника — 15 °С. Визначити термічний ККД циклу і роботу ізотермічного розширення.
2.2.15. Температура котла ТЕЦ дорівнює 350°С, температура холодильника — 10°С. Визначити максимальну теоретично можливу потужність ТЕЦ, якщо вона споживає за добу 400 кг кам'яного вугілля з питомою теплотою згоряння 3,3×107 Дж/кг.
2.2.16. * Холодильник споживає потужність 800 Вт. За 15 хв у холодильнику замерзає 3 л води, що має початкову температуру 10 °С. Визначити кількість теплоти, яку холодильник передасть навколишньому середовищу.
2.2.17. Вважаючи двигун автомобіля ідеальною тепловою машиною, визначити потужність, яку він розвиває, якщо за 1 год двигун споживає 5 кг бензину з питомою теплотою згоряння 6-10 Дж/кг. Температура роботи газів у циліндрах двигуна дорівнює 500°С, а температура відпрацьованих газів — 100 °С.
2.2.18. * Ідеальна холодильна машина, яка працює за зворотним циклом Карно, робить за один цикл роботу 37 кДж, беручи теплоту від тіла з температурою '— 10 °С та передаючи теплоту тілу з температурою 17 °С. Знайдіть кількість теплоти, взяту з холодного тіла за один цикл, і кількість теплоти, віддану гарячому тілу за один цикл.
2.2.19. * Один кіломоль ідеального газу бере участь у циклі, який складається з двох ізобар і двох ізохор. При цьому тиск газу змінюється від 100 до 100 кПа, а об'єм від 15 до 50 м3. У скільки разів робота, здійснювана при такому циклі, менша за роботу, здійснювану в циклі Карно, ізотерми якого відповідають найбільшій і найменшій температурам розглянутого циклу, а об'єм при ізотермічному розширенні збільшується вдвічі?
2.2.20. Один кіломоль двохатомного газу нагрівається так, що його абсолютна термодинамічна температура збільшується в 1,5 разу. Визначити зміну ентропії при ізобаричному й ізохоричному нагріванні газу.
2.2.21. Повітря об'ємом 1 м3перебуває за температури 0°С і тиску 98 кПа. При ізотермічному процесі об'єм повітря збільшується вдвічі. Визначити зміну ентропії повітря в цьому процесі.
2.2.22. * Визначити зміну ентропії при перетворенні 10м3 льоду, що перебуває за температури 10 °С, на пару за температури 100 °С.
2.2.23. Кисень масою 10 г нагрівається від температури 50 °С до температури 150 °С. Визначити зміну ентропії при ізобаричному й ізохоричному нагріванні газу.
2.2.24. Азот масою 10,5г ізотермічне розширюється від об'єму 1 л до об'єму 5 л. Визначити зміну ентропії газу.
2.2.25. Гелій масою 8 г ізобаричне розширюється від об'єму 10л до об'єму 15 л. Визначити зміну ентропії газу.
2.2.26. Визначити зміну ентропії при переході 6 г водню від об'єму 10 л під тиском 150 кПа до об'єму 50л під тиском 100 кПа.
2.2.27. * Лід масою І кг при температурі 0°С перетворюється на воду при тій самій температурі за допомогою пари з температурою 100 °С. Визначити масу витраченої при цьому пари і зміну ентропії системи лід — пара.
2.2.28. * Змішали 5 кг води за температури 10 °С з 8 кг води за температури 80 °С. Визначити температуру суміші і зміну ентропії при змішуванні.
2.2.29. Одноатомний газ виконує зворотний ізотермічний процес за температури 300 К. У ході цього процесу газ виконує роботу 900 Дж. Визначити зміну ентропії газу.
2.2.30. Знайти температуру азоту масою 1 г, який займає об'єм 90 см3 під тиском 0,1 МПа. Розглянути: 1) ідеальний газ; 2) реальний газ.
2.2.31. Один кіломоль реального газу кисню перебуває за температури 17°С і тиску І0МПа. Знайти об'єм газу.
2.2.32. Двохатомний газ, що перебуває під тиском 2 МПа і за температури 27 °С, адіабатичне стискається так, що його об'єм зменшується вдвічі. Визначити температуру і тиск газу після стискання.
2.2.33. * Газ розширюється адіабатичне так, що його тиск зменшується від 200 до 100 кПа. Потім газ нагрівається за сталого об'єму до початкової температури, при цьому його тиск стає таким, що дорівнює 122 кПа, Визначити показник адіабати і накреслити графік цих процесів у Р — V координатах.
* Задачі підвищеної складності.
Модуль 3.
Електростатика. Постійний струм.
МОДУЛЬ 3.
Електростатика. Постійний струм.
Приклади розв’язку задач
Задача 1. Дві мідні кульки масою m =8 г мають по 2,2×1024 електронів. Скільки електронів необхідно вилучити з кожної кульки, щоб сила електростатичного відштовхування компенсувала силу гравітаційного притягання? Чому дорівнює маса цих вилучених електронів? Яку долю від всіх електронів вони складають?
| Дано: | Розв’язання: |
| N1 = N2 = N0 = 2,2×1024 | Із вилученням електронів кульки будуть мати позитивний заряд
 (1)
де е =1,6×10-19 Кл – абсолютний заряд одного електрона (або протона),
N – число вилучених електронів
|
| V1 = V2 = 1 см3 = 1×10-6 м3 | |
| m1 = m2 = m = 8 г = 8×10-3 кг | |
| mе = 9,1×10-3 кг | |
| е = 1,6×10-9 Кл | |
 
|
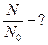
Розміри кульки невеликі (густина міді 
), ще й візьмемо відстань r між цими кульками такою, щоб кульки можна розглядати як матеріальні точки і як точкові заряди.
Між зарядженими кульками діють електростатичні (кулонівські) сили відштовхування та сили тяготіння (рис.1)
 |
Кулонівські та гравітаційні сили лежать на одній прямій й напрямлені в протилежні сторони. У рівновазі абсолютні значення цих сил однакові:
. (2)
Оскільки q1 = q2 = q і m1 = m2 = m, то
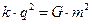, звідки
.
Тоді кількість електронів
, (3)
де е=1,6×10-19 Кл – заряд електрона.
Маса всіх вилучених електронів
. (4)
де mе – маса електрона.
Для вилучених електронів N дорівнює
(5)
Виконуємо обчислення:
.
.
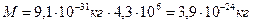Доля електронів 
.
Задача 2. Два точкові електричні заряди 1 нКл та 2 нКл перебувають у повітрі на відстані 10 см один від одного. Визначити напруженість і потенціал поля, створюваного цими зарядами в точці А, віддаленій від першого заряду на відстань 9 см та від другого заряду на 7 см.
| Дано: | Розв’язання: |
| q1 = 1 нКл = 10-9 Кл | За принципом суперпозиції полів напруженість поля в точці може бути знайдена як векторна сума напруженостей полів, створюваних кожним із зарядів окремо (рис. 2):
Напруженості полів, створюваних зарядами, дорівнюють (у повітрі e=1):
|
| q2 = -2 нКл = -2×10-9 Кл | |
| d =10 см = 0,1 м | |
| r1 = 9 см = 0,09 м | |
| r2 = 7 см = 0,07 м | |
| Е -? j -? | |
 , (1)
 . (2)
|
Вектор 
напрямлений по силовій лінії від позитивного заряду q1, вектор 
напрямлений по силовій лінії до негативного заряду q2 . Модуль вектора напруженості результуючого поля знаходимо за теоремою косинусів:
, (3)
де a - кут між векторами та (рис.1).
.
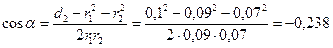Підставляючи вирази Е1 та Е2 з формул (1) і (2) у формулу (3) дістаємо:
.
Потенціал результуючого поля визначаємо згідно з принципом суперпозиції електричних полів:
.
Рис. 2
Потенціали полів, створюваних зарядами, дорівнюють
.
У даному разі маємо:
.
Виконуємо обчислення:
Задача 3. Електричне поле створюється двома зарядами 4 мкКл та -2 мкКл, що містяться на відстані 0,1 м один від одного. Визначити роботу сил поля з переміщення заряду 50нКл з точки 1 в точку 2 (рис. 3).
| Дано: | Розв’язання: |
| q1 = 4 мкКл = 4×10-6 Кл | Робота, виконувана в електростатичному полі, дорівнює:
 ,
де j1 і j2 – потенціали поля в точках 1 і 2.
|
| q2 = -2 мкКл =-2×10-6 Кл | |
| q = 50 нКл = 5×10-9 Кл | |
| а = 0,1 м | |
| А -? |
Застосовуючи принцип суперпозиції полів, визначаємо ці потенціали:
;
.
Тоді 
.
або
.
Виконуємо обчислення:
Відповідь: А = 1,43×10-2 Дж.
Задача 4. Визначити різницю потенціалів, яку має пройти в електричному полі електрон, швидкість якого дорівнює 106 м/с для того, щоб його швидкість зросла вдвічі.
| Дано: | Розв’язання: |
| u = 106 м/с | Прискорювальну різницю потенціалів можна знайти, визначивши роботу сил електростатичного поля: |
| n = 2 | |
| U -? | |
 . (4)
|
Робота сил електростатичного поля в даному випадку дорівнює зміні кінетичної енергії електрона:
. (5)
де u1 і u2 – швидкості електрона до та після проходження прискорюю чого поля відповідно.
Прирівняємо праві частини виразів (4) і (5) і одержимо
,
де 
.
Звідси різниця потенціалів
.
Виконуємо обчислення:
.
Відповідь: U = 8,53 В.
Задача 5. Визначити відстань між пластинами плоского конденсатора, якщо між ними прикладена різниця потенціалів U = 150 В, причому площа кожної пластини S = 100 см2, її заряд Q = 10 нКл. Діелектриком є слюда (e =7).
| Дано: | Розв’язання: |
| U = 150 В | Електроємність плоского конденсатора:
 .
З іншого боку електроємність визначається як:
 .
|
| S = 100 см2 = 10-2 м2 | |
| Q = 10 нКл = 10-8 Кл | |
| e = 7 | |
| d -? |
Прирівнюючи праві частини формул, отримаємо:
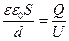, звідки 
.
Відповідь: d = 9,29 мм.
Задача 6. Різниця потенціалів між точками А та В U = 9 В (рис. 4). Електроємність конденсаторів дорівнює відповідно С1 = 3 мкФ та С2 = 6 мкФ. Визначити: 1) заряди Q1 та Q2; 2) різницю потенціалів U1 та U2 на обкладинках кожного конденсатора.
| Дано: | Розв’язання: |
| U = 9 В | Падіння напруг між точками А та В (рис.3), можна представити у вигляді:
 .
|
| С1 =3 мкФ = 3×10-6 Ф | |
| С2 =6 мкФ = 6×10-6 Ф | |
| Q1, Q2 -? U1, U2 -? |
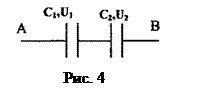Електричний заряд у послідовно з’єднаних конденсаторів однаковий, тому:
.
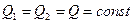Величина ємностей може бути представлена у вигляді: 
.
Звідки слідує, що 
. Падіння напруги на другому конденсаторі може бути представлене у вигляді: 
. Величина напруги між точками А та В: 
.
Величина падіння напруги на першому конденсаторі:
.
Відповідно падіння напруги на другому конденсаторі:
.
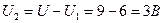Величина заряду на обкладинках конденсаторів:
.
Відповідь: Q = 27×10-6 Кл, U1 = 6 В, U2 = 3 В.
Задача 7. Внутрішній опір акумулятора 1 Ом. При силі струму 2 А його ККД дорівнює 0,5. Визначити ЕРС акумулятора.
| Дано: | Розв’язання: |
| r = 1 Ом | ККД джерела живлення:
 (1)
де R – зовнішній опір (опір навантаження).
|
| І = 2 А | |
| h = 0,8 | |
| e -? |
Звідки 
(2)
За законом Ома для повного кола
, (3)
де І – сила струму, e - ЕРС акумуляторів.
Звідки із (3) та (2) отримуємо:
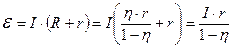. (4)
Виконуємо обчислення:
.
Відповідь: e = 10 В.
Задача 8. Потенціометр опором 100 Ом підключений до батареї з ЕРС 150 В та внутрішнім опором 50 Ом. Визначити покази вольтметра, з’єднаного з однією із клем потенціометра і контактом посередині потенціометра. Внутрішній опір вольтметра дорівнює 500 Ом.
| Дано: | Розв’язання: |
| R = 100 Ом | Показ вольтметра, відімкненого до точок А і В (рис. 5), визначаємо за законом Ома для однорідної ділянки кола:
 ,
де R1 – опір паралельно з’єднаних вольтметра і половини потенціометра;
|
| E = 150 B | |
| r = 50 Ом | |
| RV = 500 Ом | |
| U -? | |
| І – сумарна сила струму в цій частині кола (вона дорівнює силі струму в нерозгалуженій частині кола). |
Силу струму знаходимо за законом Ома для повного кола:
,
де Re – опір зовнішнього кола. Цей опір є сумою двох послідовно з’єднаних опорів:
.
Тоді 
.
Опір R1 знаходимо за формулою паралельного з’єднання провідників:
або 
; 
.
Визначаємо силу струму та покази вольтметра:
, 
.
Задача 9. Сила струму в провіднику опором 20 Ом зростає протягом 2с за лінійним законом від 0 до 6А. Визначити теплоту, що виділилася в цьому провіднику за першу і другу секунди, а також знайти відношення цих кількостей теплоти.
| Дано: | Розв’язання: |
| R = 20 Ом | Закон Джоуля-Ленца  справедливий при проходженні по провіднику постійного струму. Якщо ж сила струму в провіднику змінюється, то цей закон справджується для нескінченно малого інтервалу часу і записується у вигляді:
 (6)
|
| t = 2c | |
| I0 = 0 A | |
| t1 = 1c | |
| t2 = 2c | |
| Q1 -? Q2 -? |
Тут сила струму є деякою функцією часу. У даному випадку
, (7)
де к – коефіцієнт пропорційності, який характеризує швидкість зміни сили струму:
.
З урахуванням виразу (6) формула(7) набирає вигляду:
. (8)
Для визначення теплоти, що виділилася за скінчений інтервал часу, вираз (8) інтегруємо в необхідних межах часу:
;
.
Виконуємо обчислення:
;
.
Отже,
,
тобто за другу секунду виділиться теплоти в 7 разів більше, ніж за першу.
Задача 10. Температура вольфрамової нитки електролампи 2000 0С, діаметр 0,02 мм, сила струму 4А. Знайти напруженість поля в нитці. Питомий опір вольфраму при 00С r0 = 5,5×10-8 Ом×м, температурний коефіцієнт опору a= 5,2×10-3 К-1.
| Дано: | Розв’язання: |
| t = 2000 0С | За визначенням густини струму:
 (1)
де I – сила струму, S – площа поперечного перерізу провідника.
|
| d = 0,02 мм | |
| I = 4 A | |
| r0 = 5,5×10-8 Ом×м | |
| a = 5,2×10-3 К-1 | |
| E -? |
За законом Ома в диференціальній формі:
, (2)
де Е – напруженість електричного поля, s - питома електропровідність вольфраму.
Питомий опір провідника залежить від його температури t:
, (3)
де r0 – питомий опір при 00С,
a - температурний коефіцієнт опору.
З рівнянь (1)-(3) отримуємо:
.
Виконуємо обчислення:
.
Відповідь: Е = 8000 В/м
Задача 11. Визначити загальний опір між точками А та В кола, представленого на рис.6а, якщо R1 = 1 Ом, R2 = 3 Ом, R3 = R4 = R6 = 2 Ом, R5 = 4 Ом.
| Дано: | Розв’язання: |
| R1 = 1 Ом | 
|
| R2 = 3 Ом | |
| R3 = R4 = R6 = 2 Ом | |
| R5 = 4 Ом | |
| R -? | |
| Рис. 6а. |
Будуємо еквівалентну схему (рис.6б):
Як видно із еквівалентної схеми опори 3 та 6 з’єднані паралельно, тому величина їх еквівалентного опору:
