Цифровую систему с управлением от микроконтроллера (МК) можно рассчитать на устойчивость 2-м способом: путем замены микроконтроллера звеном чистого запаздывания е-τр.
На рисунке 10.6,а приведена структурная схема системы на базе микроконтроллера, а на рисунке 10.6,б с заменой звеном запаздывания с τ=0,01с и заданными параметрами.

Рисунок 10.6 – Структурная схема системы с управлением от МК
Для анализа устойчивости по критерию Найквиста с помощью ЛАЧХ и ФЧХ определим частоты сопряжения:

Логарифмический комплексный коэффициент передачи равен

ФЧХ с учетом τ = 0,01с системы равна


Рисунок 10.7 – ЛАЧХ и ЛФЧХ системы с МК
Из ЛАЧХ получена частота среза ωср = 400с-1 и критическая частота ωкр = 100с-1. Угол наклона ФЧХ звена запаздывания при частоте среза φτ(400) = 400 ∙ 0,01 = 4 рад = 230о.
Согласно критерия Найквиста ωкр < ωср, следовательно, система неустойчива. При уменьшении времени запаздывания τ уменьшается шаг квантования и соответственно ошибка оцифрирования.
Таким образом, использование модели звена чистого запаздывания вместо микроконтроллера дает наименьшую ошибку в том случае, если время запаздывания значительно меньше частоты среза τ << ωср.
Анализ качества по переходному процессу
Построим переходный процесс (ПП) на выходе ЦС при подаче на вход ступенчатой функции. Для нахождения сходной решетчатой функции f[nT] по ее известному z- преобразованию f(z) применят один из трех методов:
- определение бесконечного ряда для f(z) по степеням z;
- разложение f(z) на элементарные дроби;
- исследование интеграла обратного преобразования.
Рассмотрим метод разложения в степенной ряд. Обратное z-преобразование функции F(z) может быть определено разложением в бесконечный ряд по степеням z
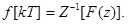
Из ранее полученного выражения  получаем
получаем
 (10.12)
(10.12)
Следовательно, коэффициенты ряда соответствуют значениям f(t) в моменты квантования.
Пример 3. Построить график ПП в системе при подаче ступенчатого входного сигнала, причем ПФ замкнутой системы равна 
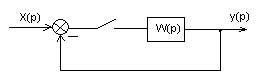
Рисунок 10.8 – Структурная схема ЦС
Для ступенчатого входного сигнала z-изображение имеет вид
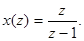
Z-изображение выходного сигнала равно
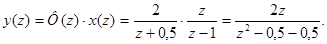
Деление числителя на знаменатель дает для y(z) бесконечный степенной ряд
Y(z) =y(0) z0 +y(1T)z-1 +y(2T)z-2+ y(3T)z-3+……..+y(nT)z-n.

Сравнивая коэффициенты (10.12) и частного от деления для одинаковых степеней z, получим
у(0) = 0; у(Т) = 2; у(2Т) = 1; у(3Т) = 1,5; у(4Т) = 1,25.
В соответствии с полученными значениями y[nT] на рисунке 3.9 показан ПП в замкнутой системе.

Рисунок 10.9 –Переходный процесс в ЦС




