Рассмотрим способ применения критерия Гурвица для исследования корней характеристического уравнения.
. (10.6)
Критерий Гурвица позволяет оценивать расположение корней характеристического уравнения многочлена относительно мнимой оси переменной р. Для определения же устойчивости в z-изображении требуется определить расположение корней относительно окружности единичного радиуса (рисунок 10.3).
Рисунок 10.3 - Отображение границы устойчивости на W-плоскости
Следовательно, необходимо сделать преобразование окружности таким образом, чтобы единичная окружность превратилась бы в мнимую ось, а внутренность единичного круга отобразилась на левую полуплоскость Re<0. Такое отображение выполняется билинейным преобразованием
. (10.7)
Заменив переменную в (10.6), получим
, (10.8)
где D(w) – многочлен степени n от новой переменной w, причем
. (10.9)
Для того, чтобы корни многочлена D(w) имели отрицательные вещественные части необходимо и достаточно, чтобы все определители Гурвица были положительными.
Рассмотрим для примера систему второго порядка n=2. Характеристическое уравнение для n=2 с учетом (10.9)
где 
; 
; 
.
Для систем второго порядка определители Гурвица будут положительными, если коэффициенты многочлена D(w) будут положительны, т.е.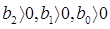 
. Система будет устойчива, если
(10.10)
Условия (10.10) для систем 2-го порядка называются критерием Шура-Кона.
Пример 1. Определить критическое значение периода квантования Ткр, при котором система будет находиться на границе устойчивости.
Рисунок 10.4 – Структурная схема импульсной системы
Определим переходную функцию непрерывной части системы
Затем с помощью таблицы 10.2 определим ее z-изображение
Разомкнутая ПФ импульсной системы равна
Знаменатель ПФ замкнутой импульсной системы является характеристическим уравнением, которое имеет вид
или z –1+10T=0.
Система будет на границе устойчивости, если
│z │= 1-10T = 1.
Отсюда Tкр = 0,2с.
Пример 2. Рассмотрим устойчивость замкнутой системы с фиксатором нулевого порядка, структурная схема которой приведена на рисунке 10.5.
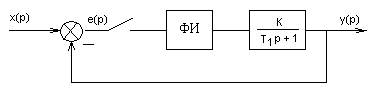
Рисунок 10.5 – Структурная схема системы
ПФ замкнутой системы равна
.
Определим ПФ звена в прямой цепи в z-изображении
где d = е(-Т/Т1).
Характеристическое уравнение системы равно
(10.11)
Поскольку характеристическое уравнение (10.11) 1-го порядка, то система будет устойчива, если для числителя 
Определим значение К, при котором система будет находиться на границе устойчивости при различных периодах квантования Т.
В этом случае
Полагая 
и разлагая в ряд 
, а также ограничившись первыми 2-мя членами ряда, получим
Условие выполняется, если
Отсюда получаем, что при (T/T1) = 0,1 Ккр = 19.
При (T/T1) = 0,2 Ккр = 9.
Таким образом, в отличие от непрерывной системы цифровая система 1-го порядка может быть неустойчивой. Устойчивость системы зависит от периода квантования Т.