При рішенні системи лінійних рівнянь алгебри може статися, що визначник системи рівний нулю або число рівнянь не рівне числу невідомих. Тому рішенню системи лінійних рівнянь алгебри повинно передувати дослідження, які виконуються в наступному порядку:
1) досліджувати чи є система рівнянь сумісною або несумісною, тобто чи має вона взагалі рішення;
2) якщо система сумісна то досліджувати чи є система рівнянь визначеною, тобто чи має вона єдине рішення або такі рішень багато;
3) якщо система сумісна і визначена знайти її єдине рішення;
4) якщо система сумісна і не визначена, то описати сукупність рішень системи.
Теорема Кронеккера-капелі
Позначимо через А матрицю системи, через С - розширену матрицю.
Система m лінійних рівнянь з n незалежними змінними сумісна тоді, коли ранг матриці А рівний рангу розширеної матриці С. Якщо ранг розширеної матриці рівний рангу матриці А і числу невідомих, тобто
r(A)= r(C)= n
то система має єдине рішення.
Якщо ранг розширеної матриці менше числа невідомих:
Г (А) - г (С) <n
то система має нескінченну безліч рішень.
Якщо ранг матриці А не рівний рангу матриці С, то система лінійних рівнянь алгебри несумісна.
Звичайні Жорданові виключення.
Розглянемо систему m лінійних функцій з n невідомими

Х1, Х2, Х3,..., Хn - незалежні змінні;
УІ, У2, У3, …, У m - залежні змінні.
Цю систему можна записати скорочено:
 де i = 1, m
де i = 1, m
Представимо систему (1) у вигляді таблиці:
| x1 | x2 | … | xis | .. | xn | |
| y1 | a11 | a12 | ... | als | ... | a1n |
| y2 | a21 | a22 | ... | a2s | ... | а2n |
| Yk | ak1 | aks | ... | aks | ... | akn |
| ym | am1 | am2 | ... | ams | ... | amn |
Така таблиця називається жордановою. Перехід від цієї таблиці до системи (1) здійснюється таким чином: елементи aKj (k=l,m) к-го рядка множаться на відповідні незалежні змінні xj (j=1,n), які розміщені у верхньому рядку. Отримані таким чином добутки складаються і прирівнюються до залежної уk (k=1,m).
Систему (1) необхідно перетворити так, щоб залежна змінна уk після перетворення стала незалежною, а незалежна змінна xs - залежною. Така операція називається одним кроком Жорданових виключень. При цьому aks -називаєтся ключовим (вирішуючим) елементом; k-й рядок називається вирішуючим рядком, s-й стовпець - називається ключовим (вирішуючим) стовпцем.
Один крок звичайних Жорданових виключень з вирішуючим (дозволяючим) елементом aks зручно розбити на наступні операції:
1) вирішуючий елемент замінюється одиницею;
2) решта елементів вирішуючого стовпця залишається без змін:
3) решту елементів вирішуючого рядка змінюють знаки на протилежних;
4) елементи, які не належать вирішуючому рядку і вирішуючому стовпцю, визначається за правилом прямокутника:
bij=aij*aks-ais*akj
де i, к-рядки; j, s - стовпці.
 | |||
1. Визначення рангу матриці за допомогою звичайних жорданових виключень
Хай дана прямокутна матриця А, яка складається з m -рядків і n -стовпців.

Складемо систему з m рівнянь, для яких коефіцієнтами при вільних змінних будуть елементи матриці А

Перепишемо цю систему в жорданову таблицю і виконаємо максимальне число кроків звичайних жорданових виключень, замінюючи залежні змінні на незалежні. Ранг матриці рівний числу максимально можливих послідовних кроків жорданових виключень (к), виконаних над жордановою таблицею, причому кожен стовпець і кожен рядок може бути вибраний не більше одного разу.
Залежні змінні уi (і = до + l,m), які не переміщаються у верхній рядок таблиці, лінійно виражаються через змінні yj (j=1, до), переміщені у верхній рядок таблиці, тобто
yi = ai1 +... + aikyk (i = до +1,m).
Теорема: Ранг добутку двох матриць не може перевищувати найменший з рангів цих матриць.
rang ([А][В]) Н min { rang [A], rang [В] }
2. Знаходження зворотної матриці за допомогою звичайних жордановых виключень.
Розглянемо не вироджену матрицю n-го порядку.

Для знаходження зворотної матриці складемо систему лінійних рівнянь, в якій роль вільних членів виконують залежні змінні

оскільки 
Запишемо цю систему в таблицю:
| Y1 | Y2 У2 | ... | yn | |
| x1 | a11 | a12 | ... | a1n |
| x2 | a21 | a22 | ... | a2n |
| xn | an1 | an2 | ... | an3 |
Послідовно над таблицею здійсним n кроків звичайних жорданових виключень. В якості ключових елементів бажано брати діагональні елементи. Дозволяють використовувати не тільки діагональні елементи, то після завершення обернена матриці необхідно упорядкувати рядки і стовпці.
III. Вирішення системи лінійних рівнянь алгебри методом звичайних жорданових виключень.
Розглянемо систему n лінійних рівнянь з n невідомими:
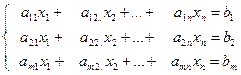
Причому rang (A)=n,
А - матриця системи;
С – розширена матриця, тобто матриця А з приєднаним справа стовпцем вільних членів.
Перепишемо систему у вигляді:

Запишемо систему в табличній формі:
| x1 | x2 У2 | … | xn | ||
| y1 | a11 | a12 | … | a1n | -b1 |
| y2 | a21 | a22 | … | a2n | -b2 |
| yn | an1 | an2 | … | an3 | -bn |
Після n послідовних кроків звичайних жордановых виключень отримаємо таблицю з вирішенням системи лінійних рівнянь алгебри:
| У1 | У2 | … | Уn | ||
| Х1 | a11 | a12 | … | а 1n |  1 1
|
| Х2 | a12 | a22 | … | a2n |  2 2
|
| Xn | an2 | an2 | … | an3 |  n n
|
Оскільки уi = 0 (i = 1,n), рішення запишемо у вигляді:
х1 = в1, х2 = в2., хn = вn
Решта коефіцієнтів таблиці складає зворотну матрицю. Якщо при знаходженні вирішень системи рівнянь не ставиться завдання знаходження зворотної матриці, то після кожного кроку звичайних жордановых виключень вирішуючий стовпець викреслюється і після n кроків таблиця приймає вигляд:
| Хj=1 | |
| ХІ |  1 1
|
| Х2 |  2 2
|
| … | … |
| Хn |  n n
|
Робота з масивами в Excel
Масив - це набір значень. Масив може бути заданий як інтервал комірок або як масив констант. Наприклад: {1; 2; 3: 4; 5; 6:, або як ім'я, що іменує інтервал або масив: 7; 8: 9).
Масив констант може складатися з чисел, тексту, логічних значень (наприклад Істина або Хибність) або значень помилок. Числа в масиві можуть бути цілими, з десятковою крапкою або експоненціальними. Масив констант може складатися з елементів різного типу, наприклад {1; 3, 4; Істина, Брехня, Істина}. Елементи масиву повинні бути константами, але не формулами. Масив констант не може містити знаки долара ($), круглих дужок і відсотки (%). Масив констант вводиться в один осередок. Щоб створити масив констант, необхідно:
· весь масив помістити в фігурні дужки ({ });
· значення стовпців розділяються комами (,);
· значення рядків розділяється крапками з комою (;).
Наприклад, замість введення чотирьох чисел (10, 20, 30, 40) в окремі комірки їх можна ввести в масив, в одну комірку у фігурних дужках {10, 20, 30, 40}, Такий масив констант є матрицею розмірності 1 на 4. Щоб представити значення " 10, 20, 30, 40" і " 50, 60, 70, 80", що знаходяться в розташованих одною під одною комірками можна створити масив констант розмірністю 2 на 4, причому рядки будуть відокремлені один від одного крапкою з комою, а значення в стовпцях - комами.
{10, 20, 30, 40; 50, 60, 70, 80}
Формула масиву може виконати декілька обчислень, а потім повернути одне значення або групу значень. Формула масиву створюється також, як і проста формула, і впливає на декілька наборів значень. Формула масиву створюється також, як і проста формула, і впливає на декілька наборів значень. Для введення формули масиву необхідно:






