Увага! При обчисленні елемента С11 матриці С слід зафіксувати стовпці в адресах комірок для елементів, що відносяться до рядка однієї матриці, та зафіксувати рядки в адресах комірок для елементів, що відносяться до стовпця другої матриці. В такому разі при розповсюджені формули помилок не буде.
А* А2 = А2*А
[А] • [Е] = [Е] • [А] = [А]
([А] • [В]) • [С] = [А] •(|В] • [С])
[А •([В] + [С])= [А] • [В] + [А] • [С]
Слід зазначити, що операція множення матриць не комутативна, тобто не завжди А*В = В*А.
Приклади:

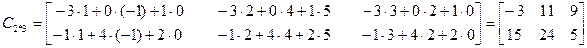
det (A • В) = det A • det В - визначник добутку матриць рівний добутку визначників цих матриць.
Мінором деякого порядку
являється визначник, який отримують шляхом умовного закреслення рядка та стовпця, на перетині яких знаходиться цей елемент:

Алгебрагічним доповненням
Деякого елемента визначника називається мінор цього елемента, помножений на коефіцієнт
(-1)р, де Р – це сума номерів рядка та стовпця, на перетині яких розміщений цей елемент:
Аij=(-1)i+j*Mij

Транспонування матриць
Транспонування матриці називається заміна рядків цієї матриці її стовпцями із збереженням їх порядку.
Матриця, отримана таким чином з матриці А називається транспонованою по відношенню до А і позначається [А]т. Для елементів транспонованих матриць виконується умова аij— аjjT. Для симетричної матриці виконуються умови Ат =А.
Функція fx - категорія Посилання на масиви -ТРАНСП(масив)- - розповсюдити на порядок mxn - - [F2]-{Ctrl-Shift-Enter] ---- повертає вертикальний діапазон комірок у вигляді горизонтального і навпаки.
Обернена матриця
Квадратна матриця [А]називається оберненою по відношенню до матриці А того ж порядку, якщо справедлива
Теорема: Для того, щоб матриця [А]-1 мала зворотну, необхідно і достатньо, щоб вона була не виродженою або невласною, тобто det А ≠ 0.
Якщо det А = 0, матриця називається виродженою або особливою.
Порядок обчислення оберненої матриці:
- обчислюється визначник матриці (det А ≠ 0);
- обчислюється допоміжна (союзна) матриця (алгебраїчні доповнення кожного елементу матриці з урахуванням знаку);
- транспонується допоміжна матриця;
- обчислюється обернена за формулою А-1=1/detA * Ат
Перевірка: А-1*А = Е (одинична матриця) + [F2]-{Ctrl-Shift-Enter]
А = Е / А-1 = Е*А
А-1 = Е / А
Функція fx - категорія Математичні – МОБР(масив) – розповсюдити на порядок mxn - - [F2]-{Ctrl-Shift-Enter] ---- повертає діапазон комірок
Обернена матриця обчислюється по правилах:
1) Обчислюється визначник матриці А.
2) Обчислюється союзна матриця, тобто матриця. складена з алгебраїчних доповнень елементів аіj матриці А:
 А11 А12 А1n
А11 А12 А1n
[ А*] = А21 А22 А2n
Аm1 Аm2 Аmn
3) Транспонується союзна матриця

 А11 А12 А1n
А11 А12 А1n
[ А] = А21 А22 А2n
Аm1 Аm2 Аmn
4) Обчислюється зворотна матриця:

Перевірка: А-1*А = Е
Визначник






