Решение задачи способом замены плоскостей проекций.

Построение.

1. Построим в плоскости треугольника АВС горизонталь и введем новую фронтальную плоскость π₄ перпендикулярно к данной горизонтали:

(hÌΔАВС)Ù(h ¤¤ p₁); p₄ ^ h;

На чертеже ось х₁ перпендикулярна горизонтальной проекции горизонтали h₁^/: х₁ ^ h₁^/; (рис.10.1)

Рис.10.1.

2.Строим новую фронтальную проекцию треугольника - А₁ ^//В₁ ^//С₁^//.

[S^// S_x^// ] [S₁^// S_x1^//]; [A^// A_x^// ] [A₁^// A_x1^//]; [B^// B_x^// ] [B₁^// B_x1^//];

[C^// C_x^//] [C₁^// C_x1^//];

По отношению к p₄ плоскость треугольника занимает проецирующее положение(рис.10.2).

Рис.10.2.

3. Из точки S₁опускаем перпендикуляр на плоскость DА₁В₁С₁, нахо­дим его основание, как точку пересечения перпендикуляра с плоскостью:

S₁K₁ 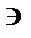S_1; S₁K₁ DА₁В₁С₁ ; S₁K₁∩DА₁В₁С₁ =K₁;

На чертеже: S₁"K₁" DA₁^// В₁^// C₁^//;

Отрезок [S₁"K₁"]определяет натуральную величину высоты пирамиды. Измеряем его и указываем размер на чертеже.

Точку К необходимо вернуть в исходное положение, зная что S₁ ^/K ^/¤¤ х (рис.10.3);

Рис.10.3.

Для того чтобы определить натуральную величину основания пирамиды-DABC, который является плоскостью общего положения, необхо­димо преобразовать его в плоскость уровня.

Для решения задачи необходимо выполнить два преобразования:

1) Преобразовать плоскость треугольника – плоскость общего положения в проецирующую плоскость.

2) Преобразовать проецирующую плоскость в плоскость уровня,

переместив ΔA₁B₁C₁ плоскопараллельным движением относительно пл. p₂ в новое положение, параллельное пл. p₁, тогда на эту плоскость он спроецируется без искажения.

a₁(A₁B₁C₁) 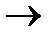a₂(A₂B₂C₂)// p₁ ;

Построение.

1. Перемещаем треугольник АВС параллельно одной из плоскостей проекций так, чтобы после преобразования он занял проецирующее положение (см. задачу №1).

2.Располагаем вырожденную фронтальную проекцию DA₂B₂C₂ –отрезок [A₂^//B₂^//C₂^//]параллельно оси х:

a₂^////х

При этом не изменится величина его фронтальной проекции:

[A₂^//B₂^//C₂^//] [A₁^//B₁^//C₁^//] (рис.11.1)

Рис.11.1.

3. Горизонтальные проекции вершин А₁^/, В₁^/, ... перемещаются в новое по­ложение А₂^/,В₂^/,.... по прямым параллельным оси х. По линиям связи строим горизонтальную проекцию DA₂B₂C₂ (ΔA₂^/B₂ C₂^/), которая конгру­энтна основанию пирамиды: [DA₂^/B₂^/ C₂^/] [DABC] (рис.11.2)

Рис.11.2.