Алгоритмы решения метрических задач.

Чтобы определить угол наклона плоскости DABC к горизонтальной плоскости проекций, необходимо переместить треугольник плоскопарал­лельным движением относительно пл.p₁ так, чтобы он заня­л положение фронтально-проецирующей плоскости:

a(DАВС)®a₁(DА₁В₁С₁)^p₂

Угол наклона вырожденной проекции треугольника DA₁^// В₁^// C₁^// на пл.p₂ к оси х определит иско­мый угол a^°.

Если необходимо определить угол наклона основания пирамиды к пл.p₂, то треугольник перемещают плоскопараллельным движением относительно фрон­тальной плоскости проекций так, чтобы DАВС занял положение горизонталь­но-проецирующей плоскости:

a(DАВС)®a₁(DА₁В₁С₁)^p₁

Тогда угол наклона вырожденной проекции треугольника DА₁^/ В₁^/ С₁^/ на пл.p₁ к оси х опре­делит искомый угол b^°.

Построение.

1. Строим горизонталь DАВС и перемещаем ее (относительно пл.p₁) в положение, перпендикулярное к пл. p₂ :

(hÌa)Ù(h ¤¤ p₁); h®h₁^/^ p₂;

На чертеже горизонтальная проекция горизонтали h₁^/ перпендикулярна оси х: h₁^/ ^ х₁; отрезок горизонтали [С₁^/ 1₁^/]@ [C^/ 1^/] (рис.8.1);

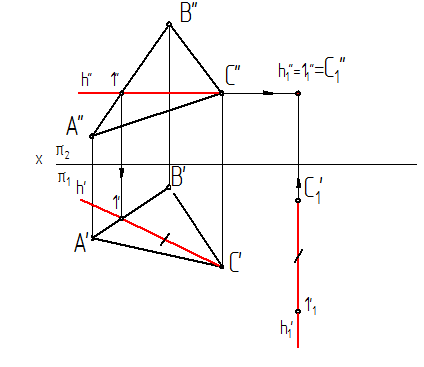
Рис.8.1.

2.Перемещаем DАВС относительно p₁ в новое положение DA₁^/ B₁^/ C₁^/, когда его горизонталь перпендикулярна пл. p₂ .

На чертеже не изменится величина го­ризонтальной проекции треугольника, т.е.DА₁^/ B₁^/ C₁^/ @ DA^/ B^/ C^/; Построения вести циркулем.

Фронтальные проекции точек А, В.... -точки А^//, В^//,... перемещаются по прямым, параллельным оси х (рис.8.2).

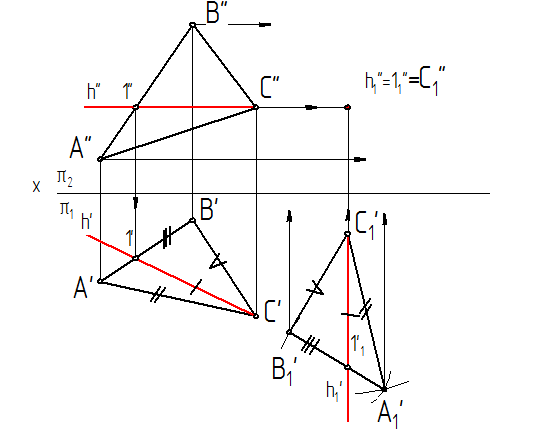
Рис.8.2.

3. По линиям связи строим новую фронтальную проекцию, которая вырождается в отрезок прямой линии [А₁^// B₁^// C₁^// ].

Угол наклона вырожденной проекции DАВС к оси х определяет искомый угол a^°. Измеряем его величину и представляем на чертеже (рис8.3).

Рис.8.3.

В положении, когда основание пирамиды (DАВС)перпендикулярно пл. p₁, отре­зок перпендикуляра, опущенного из точки S₁^/ на плоскость DА₁^/ В₁^/ С₁^/, определит иско­мую высоту пирамиды.

Если основание пирамиды перпендикулярно пл. p₂, отре­зок перпендикуляра, опущенного из точки S₁^// на плоскость DА₁^// В₁^// С₁^//, определит истинную величину высоты пирамиды.

Построение.

1.Перемещаем треугольник АВС параллельно одной из плоскостей проекций так, чтобы после преобразования он занял проецирующее положение (см. задачу №1).

2. С помощью циркуля засечками [А ' S '₁₁ ] [А'S₁'] u[C₁'S₁'] [C'S '] строим го­ризонтальную проекцию вершины пирамиды – точку S₁'. Фронтальную про­екцию токи S₁"-строим по линиям связи (рис.9.1).

Рис. 9.1.

2. Из точки S₁опускаем перпендикуляр m₁ на плоскость DА₁В₁С₁ и нахо­дим точку встречи его с плоскостью:

m₁ S_1; m₁ a₁=>m₁^// a₁^//; m₁∩a₁=K₁;

На чертеже [S₁"K₁"] DA₁^// В₁^// C₁^//; и [S₁^/ K₁^/] ¤¤ х;

Отрезок [S₁"K₁"]определяет высоту пирамиды. Измеряем его и указываем размер на чертеже.

Точку К необходимо вернуть в исходное положение, зная что:

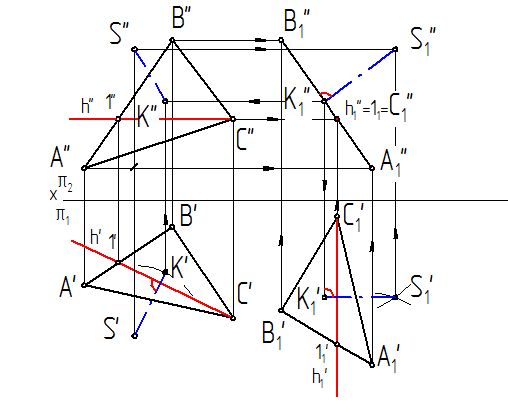
[S^/ K/ ] [S₁^/ K₁^/] и [S₁^/ K₁^/] ^/ ¤¤ х^/ (рис.9.2);