Наиболее широко метод Лауэ применяется для определения ориентации кристаллов. Установление ориентации монокристалла в слитке необходимо для ряда рентгеновских исследований и для целей практики: например, для резки монокристаллического слитка полупроводника, полученного методом вытягивания на пластины; при определении ориентировки кристаллов в прокатной трансформаторной стали и т.п.
Определение ориентировки монокристалла в пространстве осуществляется с использованием гномостереографических проекций. Для этого нужно уметь по пятнам лауэграммы построить гномостереографические проекции плоскостей. Как видно из рис.3.15, эти точки связаны между собой, поскольку лучи падающий, отраженный, а также нормаль к (hkl) всегда лежат в одной плоскости, которая пересечет рентгеновскую пленку по прямой PN. Плоскость проходит, как видно из построения, через первичное пятно P0 и включает в себя точку гномостереографической проекции M. При совмещении параллельным переносом фотопленки и плоскости гномостереографической проекции точка M1 окажется лежащей на одной прямой с первичным пятном P0 и интерференционным пятном P. Проекция M1 и пятно P будут находиться при этом по разные стороны от первичного пятна P0.
Следовательно, для построения гномостереографической проекции плоскости (hkl), необходимо провести прямую, проходящую через интерференционное пятно P и первичное P0, а затем отложить от точки P0 отрезок P0M1=OM в сторону противоположную от пятна P.
Величину отрезка OM можно легко найти с помощью сетки Вульфа, зная угол скольжения q. Из построения сетки Вульфа следует, что отрезок OM, выраженный в угловом масштабе, численно равен углу P0OH. Последний, как это видно из построения, равен 90°-q. Соответственно отрезок EM составляет в масштабе сетки Вульфа q угловых единиц. Исходя из этого, отрезок OM находят, откладывая от центра сетки Вульфа по главному меридиану угол 90°-q или от края угол q. При этом радиус сферы проекций должен быть равен радиусу сетки Вульфа.
Рис.3.15. Связь пятна лауэграммы с проекцией отражающей плоскости.
Угол скольжения q определяется как
tg2q= 
= 
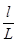, (3.25)
l - расстояние пятна от первичного;
L - расстояние кристалла до рентгеновской пленки.
В итоге построение гномостереографической проекции плоскости (hkl), давшей интерференционное пятно, осуществляется следующим образом:
1) на кальку снимают копию рентгенограммы и для каждого пятна рассчитывают угол q по формуле (3.25).
2) накладывают кальку на сетку Вульфа так, чтобы первичное пятно совпало с центром сетки, а линия P-P0 (рис.3.15) c одним из главных меридианов. По меридиану отсчитывают угол q от края или угол (90°-q) от центра сетки Вульфа.
Для определения ориентации кристалла в пространстве проводят индицирование рентгенограммы. Для этого строят на кальке гномостереографические проекции наиболее ярко выраженной на лауэграмме зоны, затем накладывают эту кальку на сетку Вульфа и, вращая вокруг общего центра, добиваются, чтобы все точки проекции попали на один меридиан (рис.3.16). В этом случае выход оси зоны мы выведем на экватор сетки Вульфа. Если затем по дугам параллелей выносят точки проекций на диаметр большого круга, то выход оси зоны сместится в центр плоскости проекций (сетки Вульфа) и проекция должна совпасть с одной из стандартных полюсных фигур. Тогда каждой точке нашего построения приписываем тот индекс, который имеет совмещенное с ней пятно полюсной фигуры. На этом индицирование заканчивается.
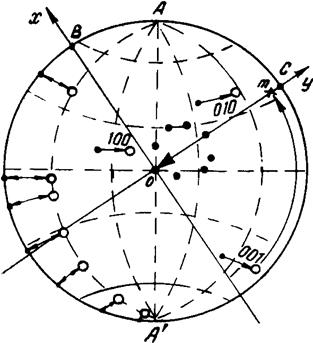
Рис.3.16. Поворот точек гномостереографических проекций на основной круг.
При индицировании пятен рентгенограммы мы одновременно переносим с полюсной фигуры на кальку положение проекций (100), (010), (001). После этого возвращают все точки 100, 010, 001 в прежнее положение поворотом по параллелям сетки на тот же угол (рис.3.16). Это позволяет определить выходы осей [100], [010], [001] в положение нашего кристалла при съемке, а, следовательно, найти углы между плоскостями (001), (010), (001) кристалла и внешними осями z (направлением рентгеновского пучка), y (следом нити, перпендикулярной S0), и x (третьей ортогональной осью). Для этого по сетке Вульфа находят углы между точками B,O,C и выходами внутренних кристаллографических осей. Например, углы плоскости (100) с осями x, y и z есть углы между точками проекций 100 и B, 100 и С, 100 и O. Как найти углы между двумя гномостереографическими проекциями показано выше.
Найдя углы между плоскостями (100), (010), (100) и внешними осями, мы тем самым определяем ориентацию кристалла в пространстве.
Вторым этапом ориентировки является определение углов, на которые нужно повернуть кристалл, чтобы пучек рентгеновских лучей S0 падал параллельно одной из главных кристаллографических осей, например [001].
Допустим, мы определили из лауэграммы, что ось [001] или [hkl] щриентирована к S0 так, как это представлено на рис.3.17. Построим гномостереографическую проекцию плоскости (001). Выход нормали к (001) соответствует выходу оси [001] на сферу, т.е. точке H. Тогда гномостереографическая проекция плоскости (001) есть точка M. Чтобы совместить ось [001] с осью z || S0, повернем ее вокруг z до плоскости yz. Получим точку D. При этом гномостереографическая проекция плоскости - точка M повернется вокруг точки О основного круга проекции по окружности в точку m. Далее поворачиваем ось [001] в плоскости yz вокруг оси x до совмещения с осью z. Точка проекция m при этом по оси y переместится в центр сферы.
Рис.3.17. Поворот кристаллографической оси [hkl] в положение, параллельное пучку.
На рабочем рисунке – кальке (рис.3.16), которая есть не что иное, как основной круг проекций, углы между точками проекций 001 и m, а также m и О определяют углы поворота кристалла в гониометрической головке вокруг осей z и x, т.е. неограненный кристалл можно точно установить по лауэграмме.
