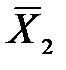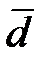Если разность двух генеральных средних оценивается по выборкам, то она, эта разность, является случайной величиной и имеет ошибку (Рисунок 21). Для генеральной разницы также можно указать доверительный интервал.
Для этого сначала надо вычислить объединенное среднеквадратичное отклонение:
(21)
Тогда доверительный интервал находится в пределах
от 
до 
(22)
где t – критическое значение двустороннего t -критерия Стъюдента для заданного α и (п1+ п2 -1) степеней свободы.
Рисунок 21. Ошибка генеральной разности
Интерпретация.
· Если доверительный интервал для разности средних включает в себя ноль, то принимается нулевая гипотеза о равенстве двух генеральных средних.
· Верхний и нижний предел доверительного интервала для разности может быть использован для клинической оценки разности двух средних.
Пример.При сравнении систолического артериального давления (мм.рт.ст.) в двух группах были получены следующие данные
Таблица 24. Результаты статобработки
95% доверительный интервал находится в пределах от -6,7 до -0,1 мм.рт.ст. (знак минус означает, что первая средняя меньше второй средней). Поскольку ДИ не включает ноль, различия между средними САД можно считать статистически значимыми с р <0,05. Однако, нижний предел разницы составляет всего лишь 0,1 мм.рт.ст. - ее вряд ли можно считать клинически значимой. |
Доверительный интервал для разности генеральных средних двух зависимых групп
При сравнении одних и тех же объектов «до» и «после» оценивается средняя разность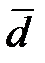 
значений признака, измеренного «до» и «после», а также среднеквадратическое отклонение этих разностей sd.
Доверительный интервал генеральной средней разности лежит в пределах
от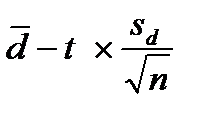 
до 
(23)
где t – критическое значение двустороннего t -критерия Стъюдента для заданного α и (п -1) степеней свободы.
Интерпретация.
· Если доверительный интервал для средней разности включает в себя ноль, то принимается нулевая гипотеза о равенстве двух генеральных средних.
· Верхний и нижний предел доверительного интервала для разности может быть использован для клинической оценки разности двух средних.
Пример.В группе из 6 человек изучалось влияние пробежки на ЧСС (уд/мин). В результате опыта получилось 2 вариационных ряда ЧСС: первый – до пробежки, второй – после пробежки:
Таблица 25. Данные к примеру
Изменяется ли ЧСС после пробежки? Оцените статистическую и клиническую значимость полученных результатов, если известно, что ЧСС имеет нормальное распределение? Для наглядности представим данные в следующей таблице 26:
Таблица 26. Результаты статобработки
Поскольку доверительный интервал не включает ноль, с 95% вероятностью принимается альтернативная гипотеза о статистической значимости изменений пульса после пробежки. Выборочные данные показывают, что пульс в среднем изменился на 8,2 уд/мин. Однако, нижний предел генеральной разности средних равен 2,6 уд/мин и такое изменение нельзя считать физиологически значимым. Возможно, это связано с маленьким объемом выборки (n =6) и исследование необходимо повторить на большем количестве испытуемых. |
