Условия устойчивости на основе ЛАЧХ

Тема 7. Устойчивость различных линейных систем

Условия устойчивости на основе ЛАЧХ

 

Метод основывается на возможности суждения об устойчиво­сти замкнутой системы по взаимному расположению логарифмиче­ских амплитудной и фазовой характеристик системы в разомкнутом состоянии. Согласно критерию Найквиста, в случае, если система устойчива, точка (-1; j0) лежит слева от АФХ первого рода.

При значениях аргумента характеристического вектора W(jω) разомкнутой системы φ = - π и модуля |W(jω)| = 1 система будет находиться на границе устойчивости. При этом L(ω) = = 201g|W(jω)| = 0, т.е. логарифмическая амплитудная характери­стика (рисунок 7.1,а) пересекает ось абсцисс. Точка пересечения ха­рактеризуется частотой среза ω_с, т.е. эта частота, при которой модуль передаточной функции системы (коэффициент усиления) равен единице или частота, при которой система теряет усилительные свойства.

 

 

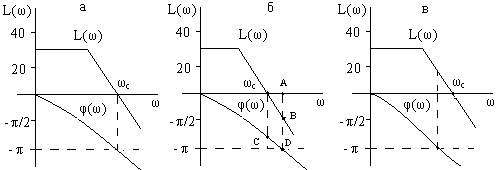
Рисунок 7.1 – Определение устойчивости по ЛАЧХ: а) на границе устойчивости; б) устойчива; в) неустойчива

 

Если система устойчива, то при φ = -π величина A(ω) = |W(jω)| < 1 и L(ω) = 201gA(ω) < 0, т.е. ордината логарифмической ампли­тудно-частотной характеристики будет иметь отрицательный знак (рисунок 7.1,б).

При неустойчивой системе углу φ = -π соответствуют вели­чины |W(jω)| > 1 и L(ω) = 201gА(ω) > 0. В этом случае ордината логарифмической амплитудной характеристики будет иметь по­ложительное значение (рис.3.1,в).

Таким образом, при амплитудно-фазовых характеристиках первого рода система будет устойчивой в том случае, если орди­ната логарифмической частотной характеристики при фазовом угле φ = -π имеет отрицательный знак. На рисунке 8.1,б показаны запас устойчивости по модулю, характеризуемый отрезком АВ, и запас устойчивости по фазе (отрезок CD).

Условия устойчивости при амплитудно-фазовой характе­ристике второго рода применительно к логарифмическим час­тотным характеристикам можно сформулировать следующим образом (рисунок 8.2).

 

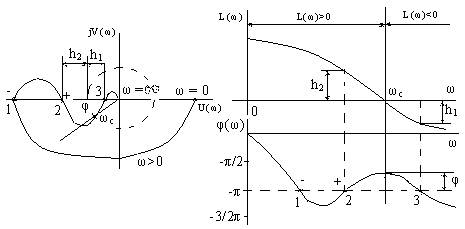
Рисунок 7.2 – АФХ второго рода и ЛАЧХ разомкнутой системы

 

Для того чтобы система, устойчивая в разомкнутом состоянии, была устойчива также и в замкнутом состоянии, необходимо и достаточно, чтобы разность между числом поло­жительных и отрицательных переходов фазочастотной характери­стики φ(ω) через прямую (-π) при тех же значениях ω, при ко­торых логарифмическая амплитудно-частотная характеристика L(ω) неотрицательна, равнялась нулю.

На рисунке 7.2 приведены амплитудно-фазовая характеристика разомкнутой системы и соответствующая ей ЛАЧХ. Из анализа этих ЛАХ и ЛЧХ видно, что разность между числом положительных и отрицательных переходов ЛФХ прямых –π при L(ω)>0 равна нулю. Следовательно, если разомкнутая система устойчива (r = 0), то и замкнутая система будет устойчива, при этом запасы устойчивости по амплитуде равны h1 и h2, а запас устойчивости по фазе равен φ.

Таким образом, в соответствии с критерием Найквиста, неустойчивая система в разомкнутом состоянии, будет устойчивой в замкнутом состоя­нии, если разность между числами положительных переходов логарифмической фазовой характеристики (ЛФХ) через прямую (-π) равна r/2 с учетом только тех значений ω, при которых ЛАЧХ положительна. Здесь r — число корней с положительной веще­ственной частью.