IІІ.Білімді бекіту. Есеп шығару

№121. Теңдеуді графиктік тәсілмен шығарыңдар:

1) х² – х – 2 = 0; х² = х + 2; у = х²; у = х + 2

Парабола мен түзудің қиылысу нүктелерінің абсциссалары, теңдеудің шешімі болады. х² – х + х – х – 2 = 0; (х + 1)(х – 2) = 0; х = −1; х = 2

2) х² – 2х – 3 = 0; у = х²; у = 2х + 3;

х² – 3х + х – 3 = 0; (х + 1)(х – 3) = 0; х = − 1; х = 3

3) х² – х + 1 = 0; шешімі жоқ

4) х² – х – 12 = 0; у = х²; у = х + 12;

х² – 4х + 3х – 12 = 0; (х + 3)(х – 4) = 0; х = -3; х = 4

№122. а-ның қандай мәнінде берілген өрнектердің мәндері тең болады?

1) 8а² – 7 және 9а² – 8; 8а² – 7 = 9а² – 8; а² = 1; а = ± 1

2) 11а – 0,5а² және 2,5а² – 25а; 11а – 0,5а² = 2,5а² – 25а

3а² – 36а =0; 3а(а – 12) = 0; а = 0; а = 12

№124. Теңдеудің сол жақ бөлігін топтау тәсілімен көбейткіштерге жіктеу арқылы шығарыңдар:

1) х² – 10х + 16 = 0; х² – 2х – 8х + 16 = 0; х(х – 2) – 8(х – 2) = 0

(х – 2)(х – 8) = 0; х = 2; х = 8

2) х² + 14х + 45 = 0; х² + 5х + 9х + 45 = 0

х(х + 5) + 9(х + 5) = 0; (х + 5)(х + 9) = 0; х = − 5; х = −9

3) х² – х + 0,24 = 0; х² – 0,6х – 0,4х + 0,24 = 0

х(х – 0,6) – 0,4(х – 0,6) = 0; (х – 0,4)(х – 0,6) = 0; х = 0,4; х = 0,6

4) х² + 7,3х + 2,1 = 0; х² + 7х + 0,3х + 2,1 = 0

х(х + 7) + 0,3(х + 7) = 0; (х + 7)(х + 0,3) = 0; х = − 7; х = − 0,3

5) х² – х – 42 = 0; х² – 7х + 6х – 42 = 0; х(х – 7) + 6(х – 7) = 0

(х + 6)(х – 7) = 0; х = − 6; х = 7

6) х² + 9х – 22 = 0; х² + 11х – 2х – 22 = 0; х(х + 11) – 2(х + 11) = 0

(х + 11)(х – 2) = 0; х = − 11; х = 2

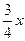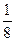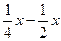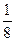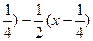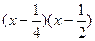7) х² – + = 0; х² – + = 0; х(х – = 0

= 0; ; ;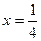

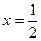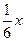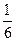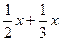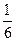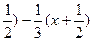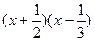8) х² – − = 0; х² – − = 0; х(х + = 0

= 0; ; ;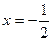

 

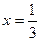қосымша материалдан. Шыныбеков – 8

№234. Теңдеуді шешіңдер:

1) х² = 64; х =±8; 2) у² = 0,09; у = ± 0,3

3) 3х² = 48; х² = 16; х = ± 4

4) х² = 3; х = ±√3; 5) у² – 10 = 39; у² = 49; у = ±7

6) х² + 5 = 30; х² = 25; х = ±5; 7) 5t² – 3 = 77; t² = 16; t=±4

8) ½*х² = 8/9; х² = 16/9; х =±4/3

№235. Теңдеудің түбірін табыңдар:

1) 2х² – 5х = 0; х(2х – 5) = 0; х = 0; х = 2,5

2) 5х² + 7х = 0; х(5х + 7) = 0; х = 0; х = − 1,4

3) 2х – 5х² = 0; х(2 – 5х) = 0; х = 0; х = 0,4

4) 4m² − 3m = 0; m(4m − 3) = 0; m = 0; m = 3/4

5) у² – 2у – 8 = 2у – 8; у² – 4у = 0; у(у – 4) = 0; у = 0; у = 4

6) 3u² + 7 = 6u + 7; 3u² – 6u = 0; 3u(u – 2) = 0; u = 0; u = 2

 

ІV. Қорытынды.Оқушылардың тақырыпты білу нәтижесін сұрақ-жауап арқылы анықтап, нақтылау.

Квадрат түбір дегеніміз не?

Квадрат теңдеудің анықтамасы

Квадрат теңдеудің түрлері

V.Үйге тапсырма. №121(2,4);№122(2); №124(2;4; 6; 8)

VI.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

8 – сынып. Алгебра

Сабақ – 22. мерзімі –

 

Сабақтың тақырыбы: Есеп шығару

Сабақтың мақсаты: Квадрат теңдеуге келтірілетін есептердің ерекшеліктеріне назар аударып, оны шешу жолдарын түсіндіру

а) Білімділік: Квадрат теңдеу және квадрат теңдеуге келтірілетін есептерді шешуді үйрету

ә) Дамытушылық: Квадрат теңдеулерді және оған келтірілетін есептердің шешу жолдарын білу

б) Тәрбиелік: Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Сабақтың әдісі: практикалық

Сабақтың типі: игеру

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын,дайындығын тексеру.Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Квадрат түбір дегеніміз не?

Квадрат теңдеудің анықтамасы

Квадрат теңдеудің түрлері

Үй тапсырмасын тексеру №121(2; 4); №122 (2); №124(2; 4; 6; 8)

№121. Теңдеуді графиктік тәсілмен шығарыңдар:

2) х² – 2х – 3 = 0; у = х²; у = 2х + 3; Парабола мен түзудің қиылысу нүктелерінің абсциссалары, теңдеудің шешімі болады.

х² – 3х + х – 3 = 0; (х + 1)(х – 3) = 0; х = − 1; х = 3

4) х² – х – 12 = 0; у = х²; у = х + 12;

х² – 4х + 3х – 12 = 0; (х + 3)(х – 4) = 0; х = -3; х = 4

№122. а-ның қандай мәнінде берілген өрнектердің мәндері тең болады?

2) 11а – 0,5а² және 2,5а² – 25а; 11а – 0,5а² = 2,5а² – 25а

3а² – 36а =0; 3а(а – 12) = 0; а = 0; а = 12

№124. Теңдеудің сол жақ бөлігін топтау тәсілімен көбейткіштерге жіктеу арқылы шығарыңдар:

2) х² + 14х + 45 = 0; х² + 5х + 9х + 45 = 0

х(х + 5) + 9(х + 5) = 0; (х + 5)(х + 9) = 0; х = − 5; х = −9

4) х² + 7,3х + 2,1 = 0; х² + 7х + 0,3х + 2,1 = 0

х(х + 7) + 0,3(х + 7) = 0; (х + 7)(х + 0,3) = 0; х = − 7; х = − 0,3

6) х² + 9х – 22 = 0; х² + 11х – 2х – 22 = 0; х(х + 11) – 2(х + 11) = 0

(х + 11)(х – 2) = 0; х = − 11; х = 2

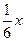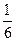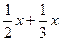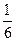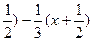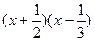8) х² – − = 0; х² – − = 0; х(х + = 0

= 0; ; ;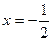

 

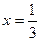IІІ. Білімді бекіту. Есеп шығару ( қосымша материалдардан. Шыныбеков.)

№238. Теңдеуді ах² + вх + с түріне келтіріңдер:

1) (х – 3)(3х + 2) = (5х – 4)(3х – 2)

3х² + 2х – 9х – 6 = 15х² – 10х – 12х + 8

12х² – 15х + 14 = 0

2) (2х + 7)(7 – 2х) = 49 + х(х + 2)

49 – 4х² = 49 + х² + 2х; 5х² + 2х = 0

 

3) 3х – 2 = 2х + 3; (3х – 2)(2х – 1) = (2х + 3)(2х + 1)

2х + 1 2х – 1 6х² – 3х – 4х + 2 = 4х² + 2х + 6х + 3

2х² – 15х – 1 = 0

4) х – 1 + 5х – 4 = 1

х + 3 4х + 1 (х – 1)(4х + 1) + (5х – 4)(х + 3) = (х + 3)(4х + 1)

4х² + х – 4х – 1 + 5х² + 15х – 4х – 12 = 4х² + х + 12х + 3

5х² – 5х – 16 = 0

5) (х – 3)(х² + 3х + 9) = х(х – 8)(х + 9)

х³ + 3х² + 9х – 3х² – 9х – 27 = х³ + 9х² – 8х² – 72х

х² – 72х + 27 = 0

6) (х + 7)(х² – 7х + 49) = х(х + 8)(х – 7)

х³ – 7х² + 49х + 7х² – 49х + 343 = х³ – 7х² + 8х² – 56х

х² – 56х – 343 = 0

№239. Теңдеуді шешіңдер:

1) 1/5*х² – 5 = 0; х² = 25; х =±5

2) 9у² – 6,25 = 0; у² = 6,25/9; у = ±5/6

3) 1,44 – х² = 3х²; 4х² = 1,44; х² = 0,36; х = 0,6

4) 5/7*х² = − 3,5 + х²; 5х² = − 24,5 + 7х²; 2х² = 24,5; х² = 12,25; х = ±3,5

5) (2у – 1)² = 10 – 4у; 4у² – 4у + 1 = 10 – 4у;

4у² = 9; у² = 9/4; у = ± 3/2

6) (3m – 2)(3m + 2) = 5m²; 9m² – 4 = 5m²;

4m² = 4; m² = 1; m = ± 1

№240. Теңдеудің түбірлерін табыңдар:

1) х² – 2х = 3х² + 2х;

4 3 3(х² – 2х) = 4(3х² + 2х)

3х² – 6х = 12х² + 8х; 9х² + 14х = 0; х(9х + 14) = 0

х = 0; 9х = − 14; х = − 14/9

2) 5у – у² = у² + 3у;

2 5 5(5у – у²) = 2(у² + 6у)

25у – 5у² = 2у² + 12у; 7у² – 13у = 0; у(7у – 13) = 0;

у = 0; у = 13/7

3) (4у – 3)² + (у + 2)² = 13; 16у² – 24у + 9 + у² + 4у + 4 = 13

17у² – 20у = 0; у(17у – 20) = 0; у = 0; у = 20/17

4) (7m + 6)(6 – 7m) = 36 − m(m + 1); 36 – 49m² = 36 − m² – m

48m² – m = 0; m = 0; m = 1/48

Қосымша.№241. теңдеуді шешіңдер:

1) (х – 2)² – 49 = 0; х – 2 =±7; х = 9; х = − 5

2) 9(2х + 3)² – 25 = 0; 2х + 3 = ± 5/3; х = 7/3; х = − 2/3

3) 2(3х + 5)² = 7(3х + 5); 2(3х + 5) = 7; 3х + 5 = 3,5; х = − 0,5

4) (3х – 1)² = 4 – 12х; (3х – 1)² = − 4(3х – 1); 3х – 1 = −4; х = − 1

ІV. Қорытынды.Оқушылардың тақырыпты білу нәтижесін сұрақ-жауап арқылы анықтап, нақтылау.

Квадрат түбір дегеніміз не?

Квадрат теңдеудің анықтамасы

Квадрат теңдеудің түрлері

V.Үйге тапсырма.№238(2; 4; 6); №239(2; 4; 6); №240(2; 4);№241(2,4);

VI.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

 

8-сынып.Алгебра.

Сабақ-23. мерзімі-

 

Сабақтың тақырыбы: §7. Квадрат теңдеу түбірлерінің формулалары

Сабақтың мақсаты: Квадрат теңдеу түбірлерінің формулаларын меңгерту

а) Білімділік: Келтірілген квадрат теңдеу және толық квадрат түбірлерінің формулалары туралы түсінік беру

ә) Дамытушылық: «Дискриминант» ұғымымен танысу, дискриминанттың мәніне байланысты квадрат теңдеудің түбірлер санын анықтау

б) Тәрбиелік: Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Сабақтың әдісі: түсіндірмелі-көрнекілік

Сабақтың типі: жаңа сабақ

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын, дайындығын тексеру. Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Теңдеу, сызықтық теңдеу, квадрат теңдеу және оның түбірлері, мәндес теңдеулер, түбір, квадрат түбірдің қасиеттері, өрнектерді түрлендіру, екі өрнектің қосындысының және айырымының квадраты

Үй тапсырмасы

№238. Теңдеуді ах² + вх + с түріне келтіріңдер:

2) (2х + 7)(7 – 2х) = 49 + х(х + 2)

49 – 4х² = 49 + х² + 2х; 5х² + 2х = 0

4) х – 1 + 5х – 4 = 1

х + 3 4х + 1 (х – 1)(4х + 1) + (5х – 4)(х + 3) = (х + 3)(4х + 1)

4х² + х – 4х – 1 + 5х² + 15х – 4х – 12 = 4х² + х + 12х + 3

5х² – 5х – 16 = 0

6) (х + 7)(х² – 7х + 49) = х(х + 8)(х – 7)

х³ – 7х² + 49х + 7х² – 49х + 343 = х³ – 7х² + 8х² – 56х

х² – 56х – 343 = 0

№239. Теңдеуді шешіңдер:

2) 9у² – 6,25 = 0; у² = 6,25/9; у = ±5/6

4) 5/7*х² = − 3,5 + х²; 5х² = − 24,5 + 7х²; 2х² = 24,5; х² = 12,25; х = ±3,5

6) (3m – 2)(3m + 2) = 5m²; 9m² – 4 = 5m²;

4m² = 4; m² = 1; m = ± 1

№240. Теңдеудің түбірлерін табыңдар:

2) 5у – у² = у² + 3у;

2 5 5(5у – у²) = 2(у² + 6у)

25у – 5у² = 2у² + 12у; 7у² – 13у = 0; у(7у – 13) = 0;

у = 0; у = 13/7

4) (7m + 6)(6 – 7m) = 36 − m(m + 1); 36 – 49m² = 36 − m² – m

48m² – m = 0; m = 0; m = 1/48

Қосымша.№241. теңдеуді шешіңдер:

2) 9(2х + 3)² – 25 = 0; 2х + 3 = ± 5/3; х = 7/3; х = − 2/3

4) (3х – 1)² = 4 – 12х; (3х – 1)² = − 4(3х – 1); 3х – 1 = −4; х = − 1

 

ІІІ.Жаңа сабақ.

х² + рх + q = 0

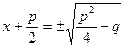
немесе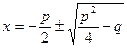

формуласы келтірілген квадрат теңдеу түбірлерінің жалпы формуласы

бірақ бұл формуланы келтірілген квадрат теңдеудің екінші коэффициенті жұп бүтін сан болғанда қолданған ыңғайлы.

ах² + вх + с = 0, мұндағы а ≠ 0

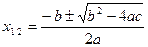
Бұл формуладағы в² – 4ас өрнегі жалпы түрдегі квадрат теңдеудің дискриминанты деп аталып, D әрпімен белгіленеді.

Квадрат теңдеудің түбірлерінің саны дискриминанттың мәніне байланысты:

1) D > 0 болса, әр түрлі екі түбірі бар. Ол түбірлер

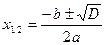
формуласымен анықталады.

2) D = 0 болса, онда теңдеудің бір-біріне тең екі түбірі бар. Бұл жағдайда теңдеудің бір түбірі бар деп, х = − в/2а формуласымен табылады.

3) D < 0 болса, теңдеудің түбірі болмайды.

Кей жағдайда квадрат теңдеудің жалпы формуласындағы екінші коэффициенті жұп сан, яғни в = 2n, мұндағы n бүтін сан болуы мүмкін. Ондай кезде

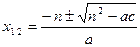
формуласы арқылы табуға болады.

IV. Білімді бекіту. Есеп шығару.

№128. Квадрат теңдеудің дискриминантын есептеп, қанша түбірі болатыны көрсетіңдер:

1) х² – 5х − 8 = 0; D>0; екі түбірі бар. 2) – х² + 6х – 11 = 0; D<0, түбірі жоқ

3) х² – 14х + 49 = 0; D=0, бір түбірі бар. 4) 3х² − х − 2 = 0; D>0, екі түбірі бар

5) − 0,5х² + 6х – 7 = 0; D>0, екі түбір 6) 0,64х² + 1,6х + 1 = 0, D=0

7) х² + 9х – 3 = 0; D>0, екі түбір 8) − 5х² + 2х – 2,5 = 0; D<0 түбірі жоқ

Теңдеуді шешіңдер:

№129.

1) х² + 3х + 2 = 0; р = 2к, D = к² – q;

D = 1,5² – 2 = 2,25 – 2 = 0,25 = 0,5²

х_1;2 = − к ±√D; х₁ = − 1,5 – 0,5; х₁ = − 2;

х₂ = − 1,5 + 0,5; х₂ = − 1

2) −х² – 2х + 24 = 0; (-1); х² + 2х – 24 = 0; в = 2n; в = 2*1,

D = 1 + 24 = 25 = 5²; х_1;2 = −1 ± 5

1 х₁ = 4; х₂ = − 6

3) х² − 7х + 12 = 0; р = 2к, D = 3,5² – 12 = 12,25 − 12 = 0,5²

х₁ = 3,5 – 0,5; х₁ = 3; х₂ = 3,5 + 0,5; х₂ = 4

4) − х² – 5х + 6 = 0; в = 2n; D = 2,5² – (-1)*6 = 6,25 + 6 = 12,25 = 3,5²

х_1;2 = 2,5 ± 3,5

−1 х₁ = 1; х₂ = − 6

№130

1) 3х² + 5х – 2 = 0; D = 25 + 24 = 7²; х₁ = 1/3; х₂ = − 2

2) 2х² – х – 3 = 0; D = 25 = 5²; х₁ = −1; х₂ = 1,5

3) 9х² − 6х + 1 = 0; D = 0; х = 1/3;

4) 5х² − 8х – 4 = 0; D = 36 = 6²; х₁ = − 2/5; х₂ = 2

V. Қорытынды.

Сабақты бекіту сұрақтары:

1) Қандай теңдеуді квадрат теңдеу дейді?

2) Квадрат теңдеудің қанша түбірі болатынын қалай анықтауға болады?

VІ.Үйге тапсырма.№128(2; 4; 6; 8),№129(2; 4), №130(2; 4),

VIІ.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

8 – сынып. Алгебра

Сабақ – 24. мерзімі –

 

Сабақтың тақырыбы: Есеп шығару

Сабақтың мақсаты: Квадрат теңдеу түбірлерінің формулаларын орынды қолдана білуді үйрету

а) Білімділік: Квадрат теңдеу түбірлерінің формулалары орынды қолдана білу

ә) Дамытушылық: Квадрат теңдеу түбірлерінің формулаларын қолданып, квадрат теңдеуді шешу дағдыларын қалыптастыру

б) Тәрбиелік: Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Сабақтың әдісі: практикалық

Сабақтың типі: игеру

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын, дайындығын тексеру. Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Квадрат теңдеу түбірлерінің формулалары

Дискриминант дегеніміз не?

Үй тапсырмасын тексеру.№128(2; 4; 6; 8),№129(2; 4), №130(2; 4),

№128. Квадрат теңдеудің дискриминантын есептеп, қанша түбірі болатыны көрсетіңдер:

2) – х² + 6х – 11 = 0; D<0, түбірі жоқ

4) 3х² − х − 2 = 0; D>0, екі түбірі бар

6) 0,64х² + 1,6х + 1 = 0, D=0

8) − 5х² + 2х – 2,5 = 0; D<0 түбірі жоқ

Теңдеуді шешіңдер:

№129.

2) −х² – 2х + 24 = 0; (-1); х² + 2х – 24 = 0; в = 2n; в = 2*1,

D = 1 + 24 = 25 = 5²; х_1;2 = −1 ± 5

1 х₁ = 4; х₂ = − 6

4) − х² – 5х + 6 = 0; в = 2n; D = 2,5² – (-1)*6 = 6,25 + 6 = 12,25 = 3,5²

х_1;2 = 2,5 ± 3,5

−1 х₁ = 1; х₂ = − 6

№130

2) 2х² – х – 3 = 0; D = 25 = 5²; х₁ = −1; х₂ = 1,5

4) 5х² − 8х – 4 = 0; D = 36 = 6²; х₁ = − 2/5; х₂ = 2

IІІ. Білімді бекіту. Есеп шығару

№ 131. Теңдеуді шешіңдер:

1) 5х² – 14х + 8 = 0; в = 2n; D = 49 – 40 = 9 = 3²; х_{1; 2} = 7 ± 3; (4/5;2)

2) 3х² − 10х + 7 = 0; в = 2*(− 5); D = 25 – 21 = 4 = 2²; х_{1; 2} = 5 ± 2; (1;7/3)

3) 9х² – 12х + 4 = 0; в =2n; D = 36 – 36 = 0; х_{1; 2} = 6/9; х_{1; 2} = 2/3

4) − 4х² – 12х +7 = 0; в = 2n; D = 36 + 28 = 64 = 8²; х_{1; 2} = 6 ± 8; (1/2;-3,5)

−4

№132. х-тің қандай мәнінде:

1) 6х² + 5х – 20 = − 9; 6х² + 5х – 11х = 0; D = 25 – 4*6*(− 11) = 289 = 17²

х_{1; 2} = − 5 ± 17; (− 11/6;1)

2) 13х² + х + 10 = 5х² + 17; 8х² + х – 7 = 0; D = 1 + 224 = 225 = 15²; х_{1; 2} = −1 ± 15; (− 1;7/8)

 

3) 3х⁴ + 4х² – 23 = − 9 + х + 3х⁴; 4х² – х – 14 = 0; D = 225 = 15²; х_{1; 2} = 1 ± 15; (− 7/4;2)

4) 10х² + 19х = 19х² + 5х + 5; 9х² – 14х + 5 = 0; в = 2n;

D = 49 – 45 = 4 = 2²; х_{1; 2} = 7 ± 2; (5/9;1)

№133. Теңдеуді шешіңдер:

1) 5х² + 4х – 1 = 0; в = 2n; D = 4 + 5 = 9 = 3²; х_{1; 2} = −2 ± 3; (− 1; 1/5)

2) 3х² + 10х + 7 = 0; в = 2n; D = 25 – 21 = 4 = 2²; х_{1; 2} = − 5 ± 2; (− 7/3; −1)

3) 16х² – 2х – 5 = 0; в = 2n; D = 1 + 80 = 81= 9²; х_{1; 2} = 1 ± 9; (−1/2;5/8)

4) − 7х² – 4х + 11 = 0; в = 2n; D = 4 + 77 = 81 = 9²; х_{1; 2} = 2 ± 9; (1; − 11/7)

− 7

5) 28х² – 36х + 11 = 0; в = 2n; D = 324 – 308 = 4²; х_{1; 2} = 18 ± 4; (1/2; 11/14)

6) −23х² − 22х + 1 = 0; в =2n; D = 121+ 23 = 12²; х_{1; 2} = 11 ± 12; (1/23;−1)

7) − 49х² + 21х – 2 = 0; D = 441 – 392 = 49 = 7²; х_{1; 2} = −21 ± 7; (2/7;1/7)

−98

8) 3х² – 14х + 16 = 0; в =2n; D = 49 – 48 = 1 = 1²; х_{1; 2} = − 7 ± 13; (8/3;2)

Қосымша.№134. Теңдеуді шешіңдер:

1) 2х(5х – 7) = 2х² – 5; 10х² – 14х = 2х² – 5; 8х² – 14х + 5 = 0; в = 2n

D = 49 – 40 = 9 = 3²; х_{1; 2} = 7 ± 3; (5/4; 1/2)

2) (х + 4)² = 4х² + 5; х² + 8х + 16 = 4х² + 5; − 3х² + 8х + 11 = 0;

в = 2n; D = 16 + 33 = 49 = 7²; х_{1; 2} = −4 ± 7; (11/3;−1)

−3

3) (х – 5)² = 3х² – х + 14; х² – 10х + 25 = 3х² – х + 14; − 2х² – 9х + 11 = 0; D = 81 + 88 = 169 = 13²; х_{1; 2} = 9 ± 13; (1; -11/2)

−4

4) 9х(4х – 1) = 3х – 1; 36х² – 9х = 3х – 1; 36х² – 12х + 1 = 0; в = 2n;

D = 36 – 36 = 0; х_{1; 2} = 6/36; (1/6)

ІV. Қорытынды.Оқушылардың тақырыпты білу нәтижесін сұрақ-жауап арқылы анықтап, нақтылау.

Квадрат теңдеу түбірлерінің формулалары

Дискриминант дегеніміз не?

V.Үйге тапсырма.№131(2; 4); №132(2; 4); №133(2; 4; 6; 8); №134 (2; 4)

VI.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

8-сынып.Алгебра.

Сабақ-25. мерзімі-

 

Сабақтың тақырыбы: § 8. Виет теоремасы

Сабақтың мақсаты: Виет теоремасы туралы түсінік беру

а) Білімділік: Квадрат теңдеудің түбірлерінің қасиеттері, Виет теоремасы туралы түсінік

ә) Дамытушылық: Виет теоремасы және Виет теоремасына кері теореманы пайдаланып есеп шығару дағдыларын қалыптастыру

б) Тәрбиелік: Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Сабақтың әдісі: түсіндірмелі-көрнекілік

Сабақтың типі: жаңа сабақ

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын,дайындығын тексеру.Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Квадрат түбір, квадрат теңдеу, квадрат теңдеудің түрлері, дискриминант, квадрат теңдеудің түбірлерінің формуласы

Үй тапсырмасы.№131(2; 4); №132(2; 4); №133(2; 4; 6; 8); №134 (2; 4)

№ 131. Теңдеуді шешіңдер:

2) 3х² − 10х + 7 = 0; в = 2*(− 5); D = 25 – 21 = 4 = 2²; х_{1; 2} = 5 ± 2; (1;7/3)

4) − 4х² – 12х +7 = 0; в = 2n; D = 36 + 28 = 64 = 8²; х_{1; 2} = 6 ± 8; (1/2;-3,5)

−4

№132. х-тің қандай мәнінде:

2) 13х² + х + 10 = 5х² + 17; 8х² + х – 7 = 0; D = 1 + 224 = 225 = 15²; х_{1; 2} = −1 ± 15; (− 1;7/8)

 

4) 10х² + 19х = 19х² + 5х + 5; 9х² – 14х + 5 = 0; в = 2n;

D = 49 – 45 = 4 = 2²; х_{1; 2} = 7 ± 2; (5/9;1)

№133. Теңдеуді шешіңдер:

2) 3х² + 10х + 7 = 0; в = 2n; D = 25 – 21 = 4 = 2²; х_{1; 2} = − 5 ± 2; (− 7/3; −1)

4) − 7х² – 4х + 11 = 0; в = 2n; D = 4 + 77 = 81 = 9²; х_{1; 2} = 2 ± 9; (1; − 11/7)

− 7

6) −23х² − 22х + 1 = 0; в =2n; D = 121+ 23 = 12²; х_{1; 2} = 11 ± 12; (1/23;−1)

8) 3х² – 14х + 16 = 0; в =2n; D = 49 – 48 = 1 = 1²; х_{1; 2} = − 7 ± 13; (8/3;2)

Қосымша.№134. Теңдеуді шешіңдер:

2) (х + 4)² = 4х² + 5; х² + 8х + 16 = 4х² + 5; − 3х² + 8х + 11 = 0;

в = 2n; D = 16 + 33 = 49 = 7²; х_{1; 2} = −4 ± 7; (11/3;−1)

−3

4) 9х(4х – 1) = 3х – 1; 36х² – 9х = 3х – 1; 36х² – 12х + 1 = 0; в = 2n;

D = 36 – 36 = 0; х_{1; 2} = 6/36; (1/6)

ІІІ.Жаңа сабақ.

х² + рх + q = 0

формуласы келтірілген квадрат теңдеу түбірлерінің жалпы формуласы

Теорема. Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал көбейтінділері бос мүшеге тең

х₁ + х₂ = − р; х₁*х₂ = q бұл теорема Виет теоремасы деп аталады.

Мысалы: х² – 8х + 15 = 0 х₁ + х₂ = 8; х₁*х₂ = 15; х₁ = 3; х₂ = 5

Виет теоремасына кері теорема:

Егер екі санның қосындысы − р-ға, ал олардың көбейтіндісі q-ға тең болса, онда ол сандар х² + рх + q = 0 теңдеуінің түбірлері болады.

Мысалы: Егер 11 және − 2 сандары келтірілген квадрат теңдеудің түбірлері болса, онда квадрат теңдеуді құрайық

х₁ = 11, х₂ = − 2

11 – 2 = 9; 11*(− 2) = − 22;

х₁ + х₂ = 9; х₁*х₂ = − 22; х² – 9х − 22 = 0

IV. Білімді бекіту. Есеп шығару

№147. Түбірлердің қосындысы мен көбейтіндісін табыңдар:

1) х² – 6х + 8 = 0 х₁ + х₂ = 6; х₁*х₂ = 8;

2) х² − 5х + 6 = 0 х₁ + х₂ = 5; х₁*х₂ = 6;

3) х² + 2х − 3 = 0 х₁ + х₂ = − 2; х₁*х₂ = − 3;

4) х² − 7х + 2 = 0 х₁ + х₂ = 7; х₁*х₂ = 2;

5) х² − 6х + 5 = 0 х₁ + х₂ = 6; х₁*х₂ = 5;

6) х² − х − 30= 0 х₁ + х₂ = 1; х₁*х₂ = − 30

№148. Белгілі түбірлері бойынша квадрат теңдеу құрыңдар:

1) 2 және 3; х₁ = 2, х₂ = 3; 2 + 3 = 5; 2* 3 = 6;

х₁ + х₂ = 5; х₁*х₂ = 6; х² − 5х + 6 = 0;

2) 6 және 2 х₁ = 6, х₂ = 2; 6 + 2 = 8; 6* 2 = 12;

х₁ + х₂ = 8; х₁*х₂ = 12; х² – 8х + 12 = 0;

3) 5 және 3; х₁ = 5, х₂ = 3; 5 + 3 = 8; 5* 3 = 15;

х₁ + х₂ = 8; х₁*х₂ = 15; х² − 8х + 15 = 0;

4) 1 және 2 х₁ = 1, х₂ = 2; 1 + 2 = 3; 1* 2 = 2;

х₁ + х₂ = 3; х₁*х₂ = 2; х² – 3х + 2 = 0

5) 1/2 және 1/4 х₁ = 1/2, х₂ = 1/4; 1/2 + 1/4 = 3/4; 1/2* 1/4 = 1/8;

х₁ + х₂ = 3/4; х₁*х₂ = 1/8; х² − 3/4*х + 1/8 = 0;

6) 0,4 және 0,2 х₁ = 0,4, х₂ = 0,2; 0,4 + 0,2 = 0,6; 0,4*0,2 = 0,08;

х₁ + х₂ = 0,6; х₁*х₂ = 0,08; х² – 0,6х + 0,08 = 0;

7) 5/2 және 3/2 х₁ = 5/2, х₂ = 3/2; 5/2 + 3/2 = 4; 5/2* 3/2 = 15/4;

х₁ + х₂ = 4; х₁*х₂ = 15/4; х² − 4х + 15/4 = 0;

8) 3/5 және 3/5 х₁ = 3/5, х₂ = 3/5; 3/5 + 3/5 = 6/5; 3/5* 3/5 = 9/25;

х₁ + х₂ = 6/5; х₁*х₂ = 9/25; х² – 6/5х + 9/25 = 0

9) 1 және 1 х₁ = 1, х₂ = 1; 1 + 1 = 2; 1* 1 = 1;

х₁ + х₂ = 2; х₁*х₂ = 1; х² − 2х + 1 = 0;

10) 5 және 0 х₁ = 5, х₂ = 0; 5 + 0 = 5; 5* 0 = 0;

х₁ + х₂ = 5; х₁*х₂ = 0 х² – 5х = 0;

11) 0 және 1 х₁ = 0, х₂ = 1; 0 + 1 = 1; 0* 1 = 0;

х₁ + х₂ = 1; х₁*х₂ = 0; х² − х = 0;

12) 5 және 5 х₁ = 5, х₂ = 5; 5 + 5 = 10; 5* 5 = 25;

х₁ + х₂ = 10; х₁*х₂ = 25; х² – 10х + 25 = 0

№149. Берілген сандар квадрат теңдеудің түбірлері болатынын тексеріңдер:

теңдеу	х2 + 4х – 77 = 0	3х2 + 7х – 6 = 0	6х2 – 7х + 2 = 0	4х2 – 5х = 0
сандар	7; − 11	− 3; 2/3	½; 2/3	0; 5/4

Болады.

№150. Квадрат теңдеу түбірлерінің формуласын қолданбай, квадрат теңдеудің түбірлерін табыңдар:

1) х² − 10х + 25 = 0; х₁ + х₂ = 10; х₁*х₂ = 25; х₁ = 5; х₂ = 5

2) х² + 6х + 9 = 0; х₁ + х₂ = − 6; х₁*х₂ = 9; х₁ = − 3; х₂ = − 3

3) 4х² − 12х + 9 = 0; х₁ + х₂ = 3; х₁*х₂ = 9/4; х₁ = 3/2; х₂ = 3/2

4) 9х² − 24х + 16 = 0; х₁ + х₂ = 8/3; х₁*х₂ = 16/9; х₁ = 4/3; х₂ = 4/3

V. Қорытынды.

Виет теоремасын және Виет теоремасына кері теореманы тұжырымдаңдар

VІ.Үйге тапсырма.№147(2; 4; 6), №148(2; 4; 6; 8; 10; 12), №150(2; 4),

VІI.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

8 – сынып. Алгебра

Сабақ – 26. мерзімі –

 

Сабақтың тақырыбы: Есеп шығару

Сабақтың мақсаты: Келтірілген квадрат теңдеулердің түбірлерін Виет теоремасын пайдаланып табуды меңгерту

а) Білімділік: Келтірілген квадрат теңдеу түбірлерінің формулалары, Виет теоремасы, Виет теореамасына кері теореманы үйрету

ә) Дамытушылық: Келтірілген квадрат теңдеу түбірлерінің формулаларын, Виет теоремасын және Виет теоремасына кері теореманы пайдаланып есеп шығару дағдыларын қалыптастыру

б) Тәрбиелік: Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Сабақтың әдісі: практикалық

Сабақтың типі: игеру

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын, дайындығын тексеру. Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Квадрат теңдеу түбірлерінің формулалары

Виет теоремасы

Виет теоремасына кері теорема

Үй тапсырмасын тексеру.№147(2; 4; 6), №148(2; 4; 6; 8; 10; 12), №150(2; 4),

№147. Түбірлердің қосындысы мен көбейтіндісін табыңдар:

2) х² − 5х + 6 = 0 х₁ + х₂ = 5; х₁*х₂ = 6;

4) х² − 7х + 2 = 0 х₁ + х₂ = 7; х₁*х₂ = 2;

6) х² − х − 30= 0 х₁ + х₂ = 1; х₁*х₂ = − 30

№148. Белгілі түбірлері бойынша квадрат теңдеу құрыңдар:

2) 6 және 2 х₁ = 6, х₂ = 2; 6 + 2 = 8; 6* 2 = 12;

х₁ + х₂ = 8; х₁*х₂ = 12; х² – 8х + 12 = 0;

4) 1 және 2 х₁ = 1, х₂ = 2; 1 + 2 = 3; 1* 2 = 2;

х₁ + х₂ = 3; х₁*х₂ = 2; х² – 3х + 2 = 0

6) 0,4 және 0,2 х₁ = 0,4, х₂ = 0,2; 0,4 + 0,2 = 0,6; 0,4*0,2 = 0,08;

х₁ + х₂ = 0,6; х₁*х₂ = 0,08; х² – 0,6х + 0,08 = 0;

8) 3/5 және 3/5 х₁ = 3/5, х₂ = 3/5; 3/5 + 3/5 = 6/5; 3/5* 3/5 = 9/25;

х₁ + х₂ = 6/5; х₁*х₂ = 9/25; х² – 6/5х + 9/25 = 0

10) 5 және 0 х₁ = 5, х₂ = 0; 5 + 0 = 5; 5* 0 = 0;

х₁ + х₂ = 5; х₁*х₂ = 0 х² – 5х = 0;

12) 5 және 5 х₁ = 5, х₂ = 5; 5 + 5 = 10; 5* 5 = 25;

х₁ + х₂ = 10; х₁*х₂ = 25; х² – 10х + 25 = 0

№150. Квадрат теңдеу түбірлерінің формуласын қолданбай, квадрат теңдеудің түбірлерін табыңдар:

2) х² + 6х + 9 = 0; х₁ + х₂ = − 6; х₁*х₂ = 9; х₁ = − 3; х₂ = − 3

4) 9х² − 24х + 16 = 0; х₁ + х₂ = 8/3; х₁*х₂ = 16/9; х₁ = 4/3; х₂ = 4/3

IІІ. Білімді бекіту. Есеп шығару

№ 151. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

1) 3х² + 4х − 6 = 0; х² + 4/3*х – 2 = 0; х₁ + х₂ = − 4/3; х₁*х₂ = − 2

2) −х² − 7х + 8 = 0; х² + 7х – 8 = 0; х₁ + х₂ = − 7; х₁*х₂ = − 8

3) 2х² – 5х + 1 = 0; х² − 2,5х + 0,5 = 0; х₁ + х₂ = 2,5; х₁*х₂ = 0,5

4) 5х² + х − 4 = 0; х² + 0,2х – 0,8 = 0; х₁ + х₂ = − 0,2; х₁*х₂ = − 0,8

№152. 1) Түбірлерінің қосындысы − 5, көбейтіндісі 6;

х₁ + х₂ = − 5; х₁*х₂ = 6; х² + 5х + 6= 0

2) түбірлерінің қосындысы 1/12, көбейтіндісін − 1/12 болатын квадрат теңдеу құрыңдар: х₁ + х₂ = 1/12; х₁*х₂ = − 1/12; х² – х/12 – 1/12 = 0;

№153. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:

1) 1; − 3; х₁ = 1, х₂ = − 3; 1 – 3 = − 2; 1* (− 3) = − 3;

х₁ + х₂ = − 2; х₁*х₂ = − 3; х² + 2х – 3 = 0;

2) − 0,2; − 0,3; х₁ = − 0,2, х₂ = − 0,3;

− 0,2 – 0,3 = − 0,5; − 0,2 * (− 0,3) = 0,06; х² + 0,5х + 0,06 = 0;

3) 0,3; − 0,1; х₁ = 0,3, х₂ = − 0,1;

0,3 – 0,1 = 0,2; 0,3* (− 0,1) = − 0,03; х² – 0,2х – 0,03 = 0

4) − 1; 1; х₁ = − 1, х₂ = 1; − 1 + 1 = 0; − 1* 1 = − 1;

х² − 1 = 0

5) − 4; 0; х₁ = − 4, х₂ = 0; − 4 + 0 = − 4; − 4* 0 = 0;

х² + 4х = 0;

6) 0; − 5; х₁ = 0, х₂ = − 5; 0 − 5 = − 5; 0* (− 5) = 0;

х² − 5х = 0;

7) − 0,3; 0; х₁ = − 0,3, х₂ = 0; − 0,3 + 0 = − 0,3; − 0,3* 0 = 0;

х² + 0,3х = 0;

8) 1,5; − 2; х₁ = 1,5, х₂ = − 2; 1,5 − 2 = − 0,5; 1,5* (− 2) = − 3;

х² + 0,5х − 3 = 0;

№154. Түбірлері х² + 6х + 8 = 0; теңдеуінің түбірлерін 1) 2-ге; 2) 5-ке көбейткенде шығатын сандарға тең квадрат теңдеуді құрыңдар

х₁ + х₂ = − 6; х₁ * х₂ = 8; х₁ = − 2; х₂ = − 4

1) 2-ге көбейткенде: х₁ = − 4; х₂ = − 8; х² + 12х + 32 = 0;

2) 5-ке көбейткенде: х₁ = − 10; х₂ = − 20; х² + 30х + 200 = 0

№155. 1) х² – 19х + 18 = 0; 2) х² + 17х – 18 = 0 теңдеуінің бір түбірі 1-ге тең болса, онда екінші түбірін табыңдар.

1) х₁ = 1; х₂ = 18 себебі: х₁ = 1; х₂ = с/а;

2) х₁ = 1; х₂ = − 18 себебі: х₁ = 1; х₂ = с/а;

Қосымша.

Берілген түбірлері бойынша квадрат теңдеу құрыңдар

№156 1) х₁ = √3 және х₂ = √5; х₁ = √3, х₂ = √5;

√3 + √5 = √3 + √5; √3 * √5 = √15; х² − (√3 + √5)х + √15 = 0

2) х₁ = − 7 және х₂ = − 4√3; х₁ = − 7, х₂ = − 4√3;

− 7 – 4√3 = − 7 – 4√3; − 7 * (− 4√3) = 28√3; х² + (7 + 4√3)х + 28√3 = 0

3) х₁ = 2√3 және х₂ = 3√3; х₁ = 2√3, х₂ = 3√3;

2√3 + 3√3 = 2√3 + 3√3; 2√3 * 3√3 = 18; х² − 5√3х + 18 = 0

4) х₁ = − 2 және х₂ = √5; х₁ = − 2, х₂ = √5;

− 2 + √5 = − 2 + √5; − 2 * √5 = − 2√5; х² + (2 − √5)х − 2√5 = 0

№159. Теңдеуді шығармай, түбірлерінің таңбасын анықтаңдар:

1) х² – 6х + 5 = 0; екі түбірі де оң сан.

2) х² + 4х – 5 = 0 түбірлері қарама-қарсы сандар

3) х² + 20х + 19 = 0; түбірлері теріс сан

4) х² + 2х + 1 = 0; түбірлері теріс сан

5) х² + 9х − 5 = 0; түбірлері қарама-қарсы сан

6) х² – 0х − 300 = 0; түбірлері қарама-қарсы сан

ІV. Қорытынды.

Квадрат теңдеу түбірлерінің формулалары

Виет теоремасы

Виет теоремасына кері теорема

V.Үйге тапсырма.№151(2; 4); №153(2; 4; 6; 8); №155 (2); №159(2; 4; 6)

VI.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

 

8 – сынып. Алгебра

Сабақ – 27. мерзімі – 8^А – 10.12.12. 8^Ә - 13.12.12

 

Сабақтың тақырыбы: Квадрат теңдеулерді шешуге есеп шығару

Сабақтың мақсаты: Квадрат теңдеулерді шешу формулаларын тиімді пайдалана білуді меңгерту

а) Білімділік: Келтірілген квадрат теңдеу түбірлерінің формулалары, Виет теоремасы

ә) Дамытушылық: Келтірілген квадрат теңдеу түбірлерінің формулаларын, Виет теоремасын пайдаланып есептерді тиімді жолмен шығару дағдыларын қалыптастыру

б) Тәрбиелік: Оқушылардың білімге құштарлығын ояту,төзімділікке тәрбиелеу.

Сабақтың әдісі: практикалық

Сабақтың типі: бекіту

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын, дайындығын тексеру. Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Квадрат теңдеу түбірлерінің формулалары

Виет теоремасы

Виет теоремасына кері теорема

Үй тапсырмасын тексеру.№151(2; 4); №153(2; 4; 6; 8); №155(2);№159 (2; 4; 6)

№ 151. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

2) −х² − 7х + 8 = 0; х² + 7х – 8 = 0; х₁ + х₂ = − 7; х₁*х₂ = − 8

4) 5х² + х − 4 = 0; х² + 0,2х – 0,8 = 0; х₁ + х₂ = − 0,2; х₁*х₂ = − 0,8

№153. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:

2) − 0,2; − 0,3; х₁ = − 0,2, х₂ = − 0,3;

− 0,2 – 0,3 = − 0,5; − 0,2 * (− 0,3) = 0,06; х² + 0,5х + 0,06 = 0;

4) − 1; 1; х₁ = − 1, х₂ = 1; − 1 + 1 = 0; − 1* 1 = − 1;

х² − 1 = 0

6) 0; − 5; х₁ = 0, х₂ = − 5; 0 − 5 = − 5; 0* (− 5) = 0;

х² − 5х = 0;

8) 1,5; − 2; х₁ = 1,5, х₂ = − 2; 1,5 − 2 = − 0,5; 1,5* (− 2) = − 3;

х² + 0,5х − 3 = 0;

№155. 1) х² – 19х + 18 = 0; 2) х² + 17х – 18 = 0 теңдеуінің бір түбірі 1-ге тең болса, онда екінші түбірін табыңдар.

2) х₁ = 1; х₂ = − 18 себебі: х₁ = 1; х₂ = с/а;

Қосымша.

№159. Теңдеуді шығармай, түбірлерінің таңбасын анықтаңдар:

2) х² + 4х – 5 = 0 түбірлері қарама-қарсы сандар

4) х² + 2х + 1 = 0; түбірлері теріс сан

6) х² – 0х − 300 = 0; түбірлері қарама-қарсы сан

 

IІІ. Білімді бекіту. Есеп шығару (Қосымша материал. Шыныбеков-8)

№259. Теңдеудің түбірлерін табыңдар:

1) х² + 7х − 60 = 0; D = 49 + 240 = 289 = 17²

х₁ = − 7 – 17 = − 12; х₂ = − 7 + 17 = 5

2 2 Ж: (− 12; 5)

2) у² − 10у − 24 = 0; в = 2n; D = 25 + 24 = 49 = 7²

х₁ = 5 – 7 = − 2; х₂ = 5 + 7 = 12

Ж: (5; 12)

3) m² + m − 90 = 0; D = 1 + 360 = 361 = 19²

m₁ = − 1 – 19 = − 10; m₂ = − 1 + 19 = 9

2 2 Ж: (− 10; 9)

4) 3t² + 7t + 4 = 0; D = 49 − 48 = 1= 1²

х₁ = − 7 – 1 = − 4/3; х₂ = − 7 + 1 = − 1

6 6 Ж: (− 4/3; − 1)

5) 3х² + 32х + 80 = 0; D = 1024 − 960 = 64 = 8²

х₁ = − 32 – 8 = − 20/3; х₂ = − 32 + 8 = − 4

6 6 Ж: (− 20/3; − 4)

6) 2х² + 9х − 486 = 0; D = 81 + 3888 = 3969 = 63²

х₁ = − 9 – 63 = − 18; х₂ = − 9 + 63 = 13,5

4 4 Ж: (− 18; 13,5)

7) 3х² − 6х + 3 = 0; |: 3 х² − 2х + 1 = 0; в = 2n;

D = 1 – 1 = 0; х₁ = х₂ = 1 Ж: 1

8) 9х² + 6х + 1 = 0;; в = 2n; D = 9 − 9 = 0;

х₁ = х₂ = − 3/9 = − 1/3 Ж: (− 1/3)

№262. в = 2n формуласын қолданып, теңдеуді шешіңдер:

1) 3х² − 14х + 16 = 0; в = 2n; D = 49 – 48 = 1;

х₁ = 7 – 1 = 2; х₂ = 8/3 Ж: (2; 8/3)

2) х² + 2х − 80 = 0; в = 2n; D = 1 + 80 = 81 = 9²;

х₁ = − 10; х₂ = 8 Ж: (−10; 8)

3) 15у² − 22у − 37 = 0; в = 2n; D = 121 + 555 = 676 = 26²

х₁ = − 1; х₂ = 5 + 7 = 37/15 Ж: (− 1; 37/15)

4) 5х² − 6х + 1 = 0; в = 2n; D = 9 – 5 = 4 = 2²;

х₁ = 1/5; х₂ = 1 Ж: (1/5; 1)

5) 4х² − 36х + 77 = 0; в = 2n; D = 324 – 308 = 16 = 4²;

х₁ = 7/2; х₂ = 11/2 Ж: (7/2; 11/2)

6) х² − 22х − 23 = 0; в = 2n; D = 121 + 23 = 144 = 12²;

х₁ = − 1; х₂ = 23 Ж: (−1; 23)

№292. Виет теоремасына кері теореманы қолданып, теңдеулердің түбірлерін табыңдар:

1) х² − 5х + 6 = 0; х₁ + х₂ = 5; х₁*х₂ = 6; х₁ = 2; х₂ = 3

2) х² + 4х + 3 = 0; х₁ + х₂ = − 4; х₁*х₂ = 3; х₁ = − 1; х₂ = − 3

3) х² − 16х + 48 = 0; х₁ + х₂ = 16; х₁*х₂ = 48; х₁ = 12; х₂ = 4

4) х² − 2х − 3 = 0; х₁ + х₂ = 2; х₁*х₂ = − 3; х₁ = − 1; х₂ = 3

5) х² + 3х − 4 = 0; х₁ + х₂ = − 3; х₁*х₂ = − 4; х₁ = 1; х₂ = − 4

6) х² + 12х + 27 = 0; х₁ + х₂ = − 12; х₁*х₂ = 27; х₁ = − 3; х₂ = − 9

№ 294. Түбірлері бойынша квадрат теңдеу құрыңдар:

1) − 7; − 2; х² + 9х + 14 = 0; 2) − 3,4; 6; х² − 2,6х − 20,4 = 0;

3) 4/3; 2; х² – 10/3х + 8/3 = 0 4) 8; − 3; х² − 5х − 24 = 0 5) 4/7; 4/7; х² − 8/7х + 16/49 = 0;

6) − 8/3; − 8/3 х² + 16/3х + 64/9 = 0;

7) √2; √5; х² − (√2 + √5)х + √ 10= 0;

8) 3 − √5; 3 + √5; х² −6х +4 = 0;

9) −√7; √2; х² − (√2 − √7)х −√14 = 0

ІV. Қорытынды.

Квадрат теңдеу түбірлерінің формулалары

Виет теоремасы

Виет теоремасына кері теорема

V.Үйге тапсырма.№259 (Ш. 2; 4; 6; 8); №262(Ш.2; 4; 6); №292(Ш.(2; 4; 6); №294(Ш.2; 4; 6; 8)

VI.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

8-сынып.Алгебра

Сабақ-28.мерзімі-

 

Сабақтың тақырыбы: Бақылау жұмысы.

Сабақтың мақсаты: Квадрат теңдеулер және квадрат теңдеу формулалары тақырыбы бойынша бақылау жұмысын алу

а) Білімділік: Квадрат теңдеулер және Виет теоремасы тақырыбына есептер шығару

ә) Дамытушылық: Квадрат теңдеулер формуласы мен Виет теоремасының формулаларын есеп шығару барысында пайдалана білу.

б) Тәрбиелік: Өз беттерінше ойлану қабілеттерін дамыту

Сабақтың әдісі: практикалық

Сабақтың типі: тексеру

Сабақтың көрнекілігі: сызба,жазба материалдар

Сабақтың барысы:

І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын, дайындығын тексеру. Оқушылармен амандасу.

ІІ.Өткенді қайталау.

Квадрат теңдеу формулалары

Виет теоремасы

IІІ.Бақылау жұмысы, №2

І нұсқа

1. Теңдеулердің қайсысы квадрат теңдеу болады

1) 2х² + 3х − 7 = 0; 2) х³ + 2х + 1 = 0 3) 1/2*х² + 5 = 0

4) 4х² + 6х = 0; 5) 3х⁴ + 11 = 0 6) 10х + 4 = 0

2. Теңдеуді шешіңдер:

1) х² – 81 = 0 2) 3х² = 27 3) 15х² – 375 = 0

3. Теңдеудің шешімін табыңдар:

1) 2х² + 5х + 4 = 0 2) 3х² – 22х + 7 = 0

4. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:

х₁ = 7 және х₂ = 8

5. Түбірлерінің қосындысы 3, көбейтіндісі − 2 болатын квадрат теңдеу құрыңдар

6. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

5х² – 2х − 7 = 0

ІІ нұсқа

1. Теңдеулердің қайсысы квадрат теңдеу болады

1) 15х² − 375 = 0; 2) х³ + 5х + 1 = 0 3) 2,5х² − 3х + 7 = 0

4) 1/2*х² − 7/2 = 0; 5) 5х⁴ + 3 = 0 6) 7х + 5 = 0

2. Теңдеуді шешіңдер:

1) х² – 144 = 0 2) 2х² = 8 3) 11х² – 539 = 0

3. Теңдеудің шешімін табыңдар:

1) 3х² − 5х − 2 = 0 2) 5х² – 16х + 3 = 0

4. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:

х₁ = − 1,8 және х₂ = 5

5. Түбірлерінің қосындысы 15, көбейтіндісі 54 болатын квадрат теңдеу құрыңдар

6. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

10х² – 9х − 2 = 0

І нұсқаның жауабы: 1. 1) 2х² + 3х − 7 = 0; 3) 1/2*х² + 5 = 0

4) 4х² + 6х = 0; 2. 1) х² = 81; х = ± 9;

2) 3х² = 27; х² = 9; х = ± 3; 3) 15х² = 375; х² = 25; х = ± 5

3. 1) 2х² + 5х + 4 = 0; D = 25 – 32 = – 7 < 0; Ø

2) 3х² – 22х + 7 = 0; D = 484 – 84 = 400 = 20² > 0

х₁ = 1/3; х₂ = 7

4. х₁ = 7; х₂ = 8 х₁ + х₂ = 15; х₁ * х₂ = 56

5. х₁ + х₂ = 3; х₁ * х₂ = − 2 х² – 3х – 2 = 0

6. 5х² − 2х – 7 = 0 екі жағында 5-ке бөлеміз. х² – 2/5*х – 7/5 = 0

х₁ + х₂ = 2/5; х₁ * х₂ = − 7/5

ІІ нұсқаның жауабы:

1. 1) 15х² − 375 = 0; 3) 2,5х² − 3х + 7 = 0; 4) 1/2*х² − 7/2 = 0; 2. 1) х² = 144; х = ± 12;

2) 2х² = 8; х² = 4; х = ± 2; 3) 11х² = 539; х² =49; х = ± 7

3. 1) 3х² − 5х − 2 = 0; D = 25 + 24 = 49 = 7² > 0; х₁ = − 1/3; х₂ = 2

2) 5х² – 16х + 3 = 0; D = 256 – 60 = 196 = 14² > 0

х₁ = 1/5; х₂ = 3

4. х₁ = − 1,8; х₂ = 5 х₁ + х₂ = 3,2; х₁ * х₂ = − 9

5. х₁ + х₂ = 15; х₁ * х₂ = 54 х² – 15х + 54 = 0

6. 10х² − 9х – 2 = 0 екі жағында 10-ға бөлеміз. х² – 0,9х – 0,2 = 0

х₁ + х₂ = 9/10; х₁ * х₂ = − 1/5

ІV. Қорытынды. Оқушылардың жұмыстарын тексеру.

V.Үйге тапсырма. §7,8

VІ.Бағалау.Оқушылардың білім-біліктілігін анықтап баға қою.

 

8-сынып

Бақылау жұмысы №2

І нұсқа

1. Теңдеулердің қайсысы квадрат теңдеу болады

1) 2х² + 3х − 7 = 0; 2) х³ + 2х + 1 = 0 3) 1/2*х² + 5 = 0

4) 4х² + 6х = 0; 5) 3х⁴ + 11 = 0 6) 10х + 4 = 0

 

2. Теңдеуді шешіңдер:

1) х² – 81 = 0 2) 3х² = 27 3) 15х² – 375 = 0

 

3. Теңдеудің шешімін табыңдар:

1) 2х² + 5х + 4 = 0 2) 3х² – 22х + 7 = 0

 

4. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:

х₁ = 7 және х₂ = 8

 

5. Түбірлерінің қосындысы 3, көбейтіндісі − 2 болатын квадрат теңдеу құрыңдар

 

6. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

5х² – 2х − 7 = 0

 

8-сынып

Бақылау жұмысы №2

ІІ нұсқа

1. Теңдеулердің қайсысы квадрат теңдеу болады

1) 15х² − 375 = 0; 2) х³ + 5х + 1 = 0 3) 2,5х² − 3х + 7 = 0

4) 1/2*х² − 7/2 = 0; 5) 5х⁴ + 3 = 0 6) 7х + 5 = 0

 

2. Теңдеуді шешіңдер:

1) х² – 144 = 0 2) 2х² = 8 3) 11х² – 539 = 0

 

3. Теңдеудің шешімін табыңдар:

1) 3х² − 5х − 2 = 0 2) 5х² – 16х + 3 = 0

 

4. Берілген түбірлері бойынша квадрат теңдеу құрыңдар:

х₁ = − 1,8 және х₂ = 5

 

5. Түбірлерінің қосындысы 15, көбейтіндісі 54 болатын квадрат теңдеу құрыңдар

 

6. Теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

10х² – 9х − 2 = 0

8-сынып.Алгебра

Сабақ- 29.мерзімі-

 

Сабақтың тақырыбы: Пысықтау

Сабақтың мақсаты: Квадрат теңдеулер және квадрат теңдеу формулалары тақырыбы бойынша алынған бақылау жұмысына қатемен жұмыс жасату

а) Білімділік: Квадрат теңдеулер және оның формулалары тақырыптарынан алынған бақылау жұмысының қателерімен жұмыс жасау.

ә) Дамытушылық: Дидактикалық материалдан өзіндік жұмыс пен есептер шығарту.

б) Тәрбиелік:Өз беттерінше ойлану қабілеттерін дамыту

Сабақтың әдісі: практикалық

Сабақтың типі: пысықтау, тексеру

Сабақтың көрне