Зачастую в исследованиях представляется необходимым выявить, зависит ли значение одной переменной от значения другой.
Для выявления такой взаимосвязи обычно используют тест, который называется «Хи-квадрат», когда в таблице сопряженности размещаются 2 качественные переменные. Этот тест проверяет взаимную независимость двух переменных – это называется формулировка нулевой гипотезы о независимости двух переменных (H0).
H0 - исходное предположение исследователя о том, что исследуемые переменные являются независимыми.
Гипотезе H0 ставится альтернативная гипотеза H1 - между переменными существует связь.
Тест позволяет выявить, является ли H0 верной и она принимается либо она отвергается и принимается H1.
Вычисление критерия Хи-квадрат - количественная оценка на проверку гипотезы о том, что столбцовая и строковая переменная являются независимыми.
Критерий Хи-квадрат называют критерием Пирсона. Он не определяет ни силу, ни направление связи между переменными, а лишь выявляет её наличие или отсутствие.
Для проверки нулевой гипотезы применяется следующая формула:
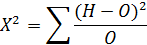
H – наблюдаемая частота
O – ожидаемая частота
Степени свободы: df = n – 1, где n – число наблюдений.
Пример:
Из 100 респондентов - 70 женщин и 30 мужчин. Известно, что 10 респондентов увлекаются искусством.
Согласно теории вероятностей ожидаемая частота для женщин - 7, для мужчин - 3.
Такие частоты называют ожидаемыми.
Если между наблюдаемой и ожидаемой частотой существуют заметные различия, то и значение Хи-квадрат возрастает.
Чем больше отклонение между частотами, тем менее вероятнее становится гипотеза
H0 о том, что переменные независимы.
Пример:
H0: у покупателей нет предпочтений
H1 у покупателей есть предпочтения.
Хи-квадрат выявляет степень согласия H и O частот. H0 принимается, когда Н ≈ О.
Необходимыми условиями проведения теста Хи-квадрат являются:
1. Случайность выборки
2. Наблюдаемая частота больше 5
Наблюдаемые частоты - то, что получили на опыте.
Ожидаемые - то, что предполагаем.
Рассматривают распределение Хи-квадрат, форма которого зависит от числа степеней свободы. При увеличении n распределение приближается к нормальному.
Вид Хи-квадрат распределения:
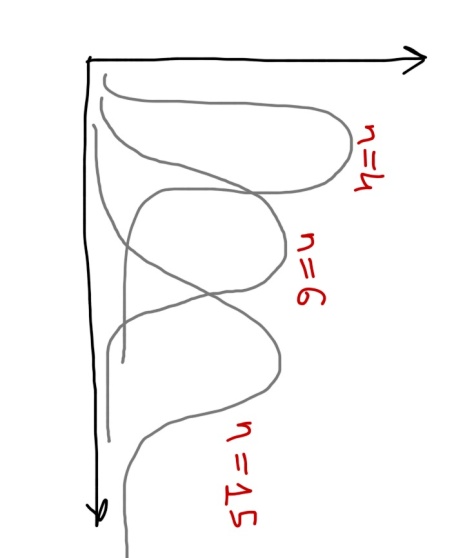
Критическая область – такая площадь под кривой Хи-квадрат распределения, для которой значение Хи-квадрат велико.
Критическая область:
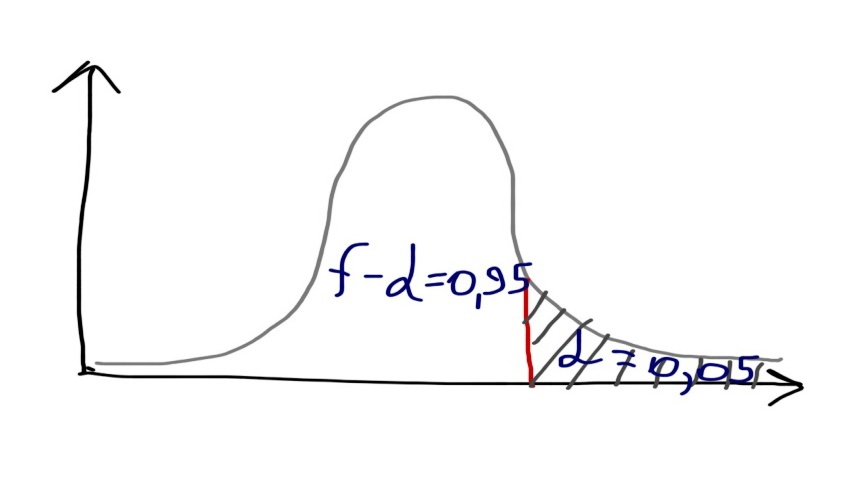
95% уверены в том, что значение Хи-квадрат попадёт в эту область.
Ошибка p > 0,05 – не значимая связь
Если p ≤ 0,05 – значимая связь
Если p ≤ 0,01 – очень значимая связь
Если p = 0,01 – сильно значимая связь
Тест осуществляется через Таблица сопряжённости – Статистики – позволяет рассчитать значение Хи-квадрат.
В файле вывода получаем таблицу «Критерий Хи-квадрат».
X2 = 8,626 означает не значимую связь.
Критерий правдоподобия является критерием, уточняющем значение Хи-квадрат. Он распространяет данные выборки на большое число наблюдений, уточняя прежде рассчитанное Хи-квадрат. Обычно значение этого критерия незначительно отличается от критерия Хи-квадрат и является уточняющим.
Зависимость линейной связи является мерой линейной зависимости между строками и столбцами таблицы сопряжённости, является уточнением Хи-квадрата.
Kn-n = X2 (n – 1)
Метод Монте-Карло может быть восстановлен через кнопку Точные. Используется в случае, если ожидаемые частоты в ячейках таблицы больше 5.
Этот метод обычно используют для больших наборов данных, где точность выполнений ограничена. Метод позволяет установить доверительный уровень (например, 95%).
Возможно определить количество выборок:
Выборки осуществляются автоматически из контрольного набора таблиц одинаковой размерности.
Коэффициент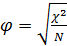 
, где N – объём выборки. Изменяется от 0 до 1.
В нашем случае значение φ = 0,142 – незначительная связь между признаками.
Если одна из переменных имеет более двух градаций, используется коэффициент Крамера. Он определяет меру силы связи между переменными.
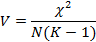
Изменяется от 0 до 1.
N – число наблюдений
K – наименьшее из чисел градации переменных
В нашем случае V = 0,142.
Лекция 22 (04.12)
Мобильные таблицы
Процедура Настраиваемые таблицы предоставляет возможность работы с категориальными переменными – данные с ограниченным циклом уникальных значений или категорий.
Категориальные переменные подразделяют на:
1. Номинальные – значение переменной как категории, не поддающейся естественному упорядочиванию.
2. Порядковые – значения переменной как категории с естественным упорядочиванием.
Категориальные переменные могут быть как символьными, так и числовыми.
Для построения мобильных таблиц необходимо предварительно определить переменные как номинальные или порядковые.
Каждое измерение мобильных таблиц задаётся либо одной переменной, либо комбинацией нескольких переменных.
Количество меток значений одной или нескольких переменных строк определяет число строк. Соответственно число переменных и количество их меток в столбцах задаёт количество столбцов.
Ячейки таблицы могут содержать частоты, средние значения, проценты, суммы и т. д.
Мобильные таблицы реализуют такие процедуры, как:
I. Состыкование – соединение отдельных таблиц в единую.
Вертикальная состыковка
| Частота | ||
| Пол | М | |
| Ж | ||
| Возраст | 25-34 | |
| 35-44 | ||
| 45-54 | ||
| 55-64 | ||
| Свыше 65 |
Горизонтальная состыковка
| Пол | Возраст | |||||
| М | Ж | 25-34 | 35-44 | 45-54 | 55-64 | Свыше 65 |
II. Таблицы сопряжённости
| Пол | |||
| М | Ж | ||
| Возраст | Ниже 24 | ||
| 25-34 | |||
| 35-44 | |||
| 45-54 | |||
| 55-64 | |||
| Свыше 65 |
III. Вложение – одна переменная вкладывается в другую в одном измерении таблицы.
Вложение предназначено для выявления связи между категориальными переменными, таким образом, вложение предоставляет информацию, идентичную информации таблицы сопряжённости.
| Частота | |||
| Возраст | Ниже 24 | М | |
| Ж | |||
| 25-34 | М | ||
| Ж | |||
| 35-44 | М | ||
| Ж |
IV. Слои – в отличие от вложения предоставляет возможность отображения только одной из категорий.
Пол Женский
| Возраст | Ниже 24 | |
| 25-34 | ||
| 35-44 |
V. Таблицы для переменных с одинаковыми категориями – используются в случае сведения воедино вопросов с одинаковыми вариантами ответов.
Общие категории сведены в столбцы
| Полностью доверяю | Частично доверяю | Не доверяю | ||
| Банкам | ||||
| Образованию | ||||
| Крупным компаниям | ||||
VI. Наборы множественных реакций – используются в случаях, когда респондент может выбрать несколько вариантов ответа.
| Частота | % по столбцу | ||
| Источник | Интернет | 26,6% | |
| Радио | 15,6% | ||
| ТВ | 15,8% | ||
| Газеты | 38,7% |
Проценты по столбцу могут превышать 100%, так как могут быть выбраны несколько вариантов. Процент высчитывается относительно всех респондентов.
VII. Вывод итогов и подытогов.
Возможен расчёт:
1) Общих итогов по строкам и столбцам
2) Итогов для подгрупп (отдельно для М и Ж)
3) Итогов для вложенных, состыкованных переменных
| Частота | ||||
| ПОЛ | Мужской | Возраст | 17-25 | |
| 26-35 | ||||
| Подытог до 35 лет | ||||
| 36-50 | ||||
| >51 | ||||
| Женский | Возраст | 17-25 | ||
| 26-35 | ||||
| Подытог до 35 лет | ||||
| 36-50 | ||||
| >51 |
VIII. Настраиваемые итожащие статистики для таблиц
Предоставляют возможность вывода частот для порядковой переменной, а также определения средних значений для этих переменных.
| Доверие к ТВ | 1. Полностью | Частота | |
| 2. Частично | Частота | ||
| 3. Не доверяю | Частота | ||
| Итого | Частота | ||
| Среднее | 2,29 |
Расчёт средних значений для нескольких переменных (ТВ и газеты) позволяет сравнить степень доверия.
Создание мобильных таблиц через Анализ – Таблицы – Настраиваемые таблицы
В мобильных таблицах можно исключать некоторые категории через диалоговое окно Настраиваемые таблицы – кнопка Категории и итоги. Здесь одна из категорий может быть исключена из содержимого при помощи Стрелки.
Лекция 23 (05.12)
