4. 
.
Підінтегральна функція задовольняє нерівність
.
Розглянемо інтеграл 
, тому він збігається. Користуючись першою ознакою порівняння, стверджуємо, що теж збігається.
5. 
.
Підінтегральна функція неперервна і додатна при 
, причому справджується така нерівність:
.
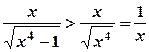Розглянемо інтеграл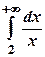 
- він розбігається 
, тому за ознакою порівняння, отримаємо, що інтеграл теж розбігається.
Невласні інтеграли другого роду (від необмежених функцій)
Як відомо, необхідною умовою інтегрованості функції на відрізку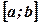 
є її обмеженість. Проте є задачі, що приводять до розгляду інтеграла від функції, яка майже на всьому відрізку обмежена і стає необмеженою поблизу деякої точки, наприклад, поблизу однієї чи обох меж. Тоді природно поширити поняття визначеного інтеграла і на такі функції, ввівши при цьому додаткові означення.
Отже, нехай функція 
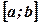задана на відрізку , крім, можливо, кінців, і є необмеженою, наприклад, поблизу точки 
, зокрема на відрізку 
, де 
. Нехай є обмеженою і інтегрованою на будь-якому відрізку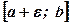 
. Точку 
при цьому називають особливою точкою функції .
Означення 1. Невласним інтегралом другого роду функції на проміжку 
називається границя 
і позначають
. (3.5)
Якщо ця границя скінчена, то інтеграл називається збіжним. Якщо границя нескінченна, або взагалі не існує, тоді інтеграл називається розбіжним. Функція при цьому називається інтегрованою на даному проміжку.
Нехай тепер функція є обмеженою і інтегрованою на будь-якому відрізку 
, і не є інтегрованою на відрізку 
.
Означення 2. Невласним інтегралом другого роду функції на проміжку 
називається границя 
і позначають
. (3.6)
У цьому випадку точка 
вважається особливою точкою функції .
Збіжність (розбіжність) інтеграла й інтегрованість функції на відповідному проміжку визначають так само, як і для інтеграла (3.5). Інші можливі випадки можуть бути зведені до вже розглянутих.
Розглянемо випадок, коли особливими точками функції є одночасно точки й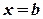 
. Це означає, що функція необмежена на та на , а на будь-якому відрізку 
вона є інтегрованою.
Тоді покладають 
, де 
- довільна точка інтервалу .
В цьому разі 
. (3.7)
Іноді може трапитися випадок, коли підінтегральна функція є необмеженою поблизу точки , яка знаходиться всередині відрізка 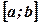. В інших частинах відрізка 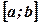функція інтегрована. Тобто точка є особливою точкою функції .
Тоді покладають , але тепер у цій рівності обидва інтеграла правої частини означаються формулами (3.5) та (3.6). Позначають: 
. (3.8)
Висновок про збіжність інтеграла 
у формулах (3.7) та (3.8) роблять тільки в тому випадку, коли обидві границі правих частин цих формул, знайдені незалежно одна від одної, існують і скінченні. Інтеграл розбігається, якщо хоча б одна з цих границь нескінченна або взагалі не існує.
Зауважимо, що ознаки збіжності невласних інтегралів другого роду аналогічні подібним ознакам для інтегралів першого роду. При дослідженні на збіжність інтегралів, де особливою точкою є точка , для порівняння використовують функції 
, інтеграл від яких 
збігається, якщо 
і розбігається, якщо 
. Якщо особливою точкою функції є точка 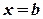, використовують функції 
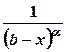, інтеграл від яких 
так само збігається при і розбігається при .
