Границя функції.
Нехай функція f(x) визначена в деякій околі x точки a крім, можливо, самої точки a. Число A є границею функції f(x) в точці a, якщо для довільного числа ε>0 існує число δ=δ(ε)>0 таке, що для всіх x є X, які задовольняють нерівність 
, виконується нерівність
Позначення: 
Це позначення можна представити геометрично: якщо A є 
, то для будь-якого околу точки А на осі ОУ існує δ-окіл точки a на осі ОХ така, що для всіх х≠ a із δ-околу відповідні значення функції попадають в ε-окіл, тобто точки графіку функції знаходяться у смузі, обмеженій прямими y=A+ε і y=A-ε
 y y=f(x)
       A+ε
|
A 2 ε
A-ε
0 a-b a a+b x
Обчислення границь
Перш ніж перейти к обчисленню границь, запишемо за допомогою символів основні теореми теорії границь.
Нагадаємо символи:
a – стала
∞ - нескінченна велика додатна
-∞ - нескінченна велика від’ємна
+0 – нескінченна мала додатна
-0 – нескінченна мала від’ємна
1) a+0=a; a0=0; 
; 
=∞
2) 
∞; 
3) a+∞=∞; a ∞=∞; ∞+∞=∞; ∞ ∞=∞
4) ∞∞=∞; 0∞=∞
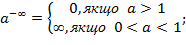
Але при обчисленні границь дуже часто з’являються так названі невизначеності. Символічно їх можна записати так:
Ці умовні записи характеризують поведінку змінних величин.
Щоб знайти границю невизначеності виразу, треба усунути цю невизначеність.
Розглянемо деякі окремі випадки.
1) Невизначеність виду 
задана відношенням двох многочленів
Тобто, щоб розкрити невизначеність , треба чисельник і знаменник розділити на найвищий степінь x у цих многочленах. При цьому можна сформувати таке правило:
1. Якщо найвищий степінь чисельника вище найвищого степеня знаменника, то границя дробу нескінченно велика.
2. Якщо найвища степінь чисельника нижче найвищого степеня знаменника, то границя дробу дорівнює нулю.
3. Якщо найвищі степені чисельника і знаменника однакові, то границя дорівнює частки від поділу коефіцієнтів біля старших степенів.
2) Невизначеність виду 
задана відношенням двох многочленів
=
Розкладемо чисельник і знаменник на множини:
Множини (x -1), через який чисельник і знаменник прямують до нуля, називають критичним множником.
Таким чином, щоб розкрити невизначеність , задану відношенням двох многочленів, треба в чисельнику і знаменнику виділити критичний множник і скоротити на нього дріб.
3) Невизначеність 
задана ірраціональними виразами.
(х-2) – критичний множник. Позбудемося від ірраціональності в чисельнику.
4) Невизначеності виду ∞-∞ задані ірраціональними виразами.
● 
● 
; 
Де e= 2,72 – ірраціональне число.
Це число грає в математиці таку ж важливу роль, як і число π. Логарифми за основою e називаються натуральними. Вони зв’язані з логарифмами за основою a.
Зауваження. При обчисленні границь, зв’язаних з числами e, застосовують таке твердження:
якщо границ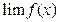і 
і 
існують і 
Приклад:
Тема 2. Правило Лопіталя.
Теорема 1. Нехай функції 
визначені і диференційовні в околі точки х0, за винятком, можливо, самої точки х0, причому
Вважатимемо, що х0 – скінчене число: 
. Довизначемо функції в точці х=х0, поклавши 
Тоді ці функції будуть неперервні в точці х0. розглянемо відрізок [x0;x], що належить даному околу. Функції 
і 
неперервні на [x0;x], диференційовні на (х0, х) і 
.
Тому за теоремою Коші знайдеться точка 
, для якої
або 
тому, що 
. Оскільки за умовою 
існує 
, якщо 
, то з рівності маємо:
Зауваження 1. Теорема справедлива і в тому випадку, коли 
. Дійсно, поклавши 
, маємо
Зауваження 2. Якщо похідні 
задовольняють ті самі умови, що і функції і 
то теорему і можна застосувати ще раз. При цьому дістанемо
Взагалі, теорему 1 можна застосувати доти, поки не прийдемо до відношення похідних 
, яке має певну границю при . Цю саму границю матиме й відношення функцій:
Теорема 1 дає змогу розкривати невизначеність виду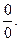 
Сформулюємо теорему, яка стосується розкриття невизначеності виду .
Теорема 2. Нехай функції і визначені і диференційовні в околі точки х0 і в цьому околі
Тоді якщо існує границя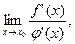 
то існує границя 
і
Цю теорему приймемо без доведення.
Виражене теоремами 1 і 2 правило обчислення границь називають правилом Лопіталя за іменем математика, який опублікував його. Але це правило відкрив І. Бернуллі, тому правило Лопіталя називають ще правилом Бернуллі – Лопіталя.
Зауважимо, що правило Лопіталя застосовується лише для розкриття невизначеності виду 
і , які називають основними. Відомі ще й такі невизначеності, як 
покажемо, як ці невизначеності зводяться до основних.
а). Якщо 
то невизначеність виду 0· 
можна звести до основних так:
або 
б). Якщо 
то невизначеність виду 
зводиться до невизначеності :
в). Якщо 
, то
і невизначеність виду 00 зводиться до невизначеності 0· , розглянутої вище. Аналогічно розкриваються невизначеності 
і 
.
Таким чином, щоб розкрити невизначеності 
, їх треба спочатку звести до основних і лише після цього застосувати правило Лапіталя.
