Нехай функція  визначена і неперервна в обмеженій замкнутій області
визначена і неперервна в обмеженій замкнутій області  . Тоді вона досягає в деяких точках свого найбільшого
. Тоді вона досягає в деяких точках свого найбільшого  і найменшого
і найменшого  значень (т.3. глобальний екстремум). Ці значення досягаються функцією в точках, розташованих усередині області, або в точках, що лежать на межі області.
значень (т.3. глобальний екстремум). Ці значення досягаються функцією в точках, розташованих усередині області, або в точках, що лежать на межі області.
Правило знаходження найбільшого і найменшого значень диференційованої в області  функції
функції  полягає в наступному:
полягає в наступному:
 1. Знайти всі критичні точки функції, що належать
1. Знайти всі критичні точки функції, що належать  і обчислити значення функції в них;
і обчислити значення функції в них;
2. Знайти найбільше і найменше значення функції  на кінцях області;
на кінцях області;
3. Порівняти всі знайдені значення функції і вибрати з них найбільше  і найменше
і найменше  .
.
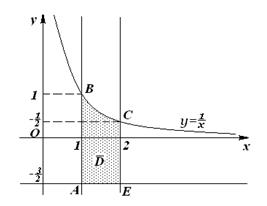
Приклад. Знайти щонайбільше і якнайменше значення функції  в замкнутій області, обмеженій лініями:
в замкнутій області, обмеженій лініями:
 ,
,  ,
,  ,
,  (див. рис.)
(див. рис.)
◄ Тут 

1. Знаходимо всі критичні точки:

Розв’язком системи є точки 
Жодна із знайдених точок не належить області  .
.
2. Досліджуємо функцію  на межі області, що складається з ділянок
на межі області, що складається з ділянок  (рис.).
(рис.).
На ділянці  :
:  ,
,  , де
, де 
 ,
,  ,
, 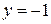 . Значення функції
. Значення функції  ,
,  .
.
На ділянці 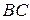 :
:
 ,
,  , де
, де  ,
,


 ,
,  . Значення функції
. Значення функції  ,
,  .
.
На ділянці 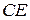 :
:  ,
, 
 ;
;  ;
;  . Значення функції
. Значення функції 

На ділянці 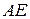 :
: 
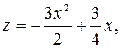
 ,
,
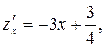

 Значення функції
Значення функції 

3. Порівнюючи отримані результати, маємо: 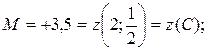 а
а
 ►
►
Тема 12. Розв’язування вправ на дослідження функції двох змінних на екстремум.
Поняття максимуму, мінімуму, екстремуму функції двох змінних аналогічні відповідним поняттям функції однієї незалежної змінної.
Приклад. Знайти екстремум функції  .
.
◄ Тут  Точки, в яких частинні похідні не існують, відсутні.
Точки, в яких частинні похідні не існують, відсутні.
Знайдемо стаціонарні точки, розв’язуючи систему рівнянь:

Звідси одержуємо точки  і
і 
Знаходимо частинні похідні другого порядку даної функції: 


В точці  маємо:
маємо:  , звідси
, звідси  тобто
тобто 
Оскільки  , то в точці функція має локальний максимум
, то в точці функція має локальний максимум

В точці  :
:  і, значить
і, значить  . Проведемо додаткове дослідження. Значення функції
. Проведемо додаткове дослідження. Значення функції  в точці
в точці 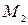 рівне нулю:
рівне нулю:  . Можна помітити, що
. Можна помітити, що  при
при  ,
,  при
при  ,
,  . Значить, в околі точки
. Значить, в околі точки  функція
функція  приймає як негативні, так і позитивні значення. Отже в точці
приймає як негативні, так і позитивні значення. Отже в точці 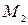 функція екстремуму не має. ►
функція екстремуму не має. ►
ПИТАННЯ ТА ЗАВДАННЯ ДЛЯ
САМОСТІЙНОГО
ОПРАЦЮВАННЯ МАТЕРІАЛУ
Тема 1. Поняття границі функції. Обчислення границь функцій.
Завдання для самоконтролю:
1.1. Знайти границю функції: а) 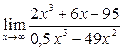 ; б)
; б) 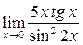 ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Питання для самоконтролю:
1. Поняття границі функції в точці.
2. Основні теореми про границі.
3. Перша важлива границя.
4. Друга важлива границя.
Тема 2. Правило Лопіталя.
Завдання для самоконтролю:
2.1. Знайти границі, використовуючи правило Лопіталя: а)  ;
;
б)  ; в)
; в)  ; г)
; г)  .
.
Питання для самоконтролю:
1. Правило Лопіталя та його наслідок.
2. Розкриття невизначеностей вигляду: 






