Взаимодействие молекул в газе, молекулы которого находятся на относительно большом расстоянии друг от друга, носит характер столкновений. От частоты столкновений зависит время протекания процессов, ведущих к установлению состояния термодинамического равновесия: диффузии, теплопроводности, электропроводности. Кроме того, от частоты соударений зависит протекание фазовых переходов в таких системах.
В действительности молекулы газа, непрерывно соударяясь друг с другом, имеют конечные размеры. Между двумя последовательными соударениями молекулы, двигаясь прямолинейно и равномерно, проходят некоторые расстояния, называемы длинами свободных пробегов. Эти расстояния могут быть самыми различными. Поэтому вводится понятие о средней длине свободного пробега.
Средняя длина свободного пробега – путь, который в среднем проходят молекулы между двумя последовательными соударениями:
,
Рис. 116.
|
где
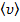- средняя скорость молекул; 
- среднее число столкновений, испытываемых одной молекулой за секунду;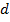 
- эффективный диаметрмолекулы, т.е. минимальное расстояние, на которое сближаются при столкновении центры двух молекул ( задаётся в таблицах) (см. рис. 116).
Так как 
, то есть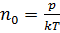 
,то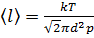 
.
Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению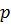 
:
.
Пример. При эффективном диаметре молекулы 
, давлении 
, температуре 
,и средней длине свободного пробега 
, с учетом того, что при этих условиях средняя скорость молекул 
, число столкновений молекулы в секунду: 
.
Упрощённое доказательство
Рис. 117.
|
Для определения частоты столкновений
считаем, что молекула имеет форму шара, и движется среди других неподвижных молекул. Эта молекула сталкивается только с теми молекулами, центры которых находятся на расстояниях 
, то есть лежат внутри «ломаного» цилиндра радиусом 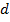(рис. 117).Среднее число столкновений за 1 секунду равно числу молекул в объёме «ломаного» цилиндра:
,
где 
- концентрация молекул, а 
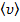где - средняя скорость молекулы, или путь, пройдённый ею за 1 секунду. Таким образом, среднее число столкновений:
.
С учетом движения других молекул: .
Тогда средняя длина свободного пробега: 
,то есть 
обратно пропорциональна концентрации молекул: 
. С другой стороны давление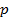 
газа прямо пропорционально концентрации молекул 
, тогда 
. Следовательно,
.
Термодинамика
Термодинамика – часть физики, в которой изучаются наиболее общие закономерности преобразования энергии.
2.1.Термодинамический метод
Термодинамика изучает макроскопические процессы в телах, не рассматривая внутреннее строение тел. Её выводы основаны на общих принципах (началах), являющихся обобщением опытных фактов. В этом смысле – термодинамика – феноменологическая теория.
Классическая термодинамика изучает равновесные состояния и квазистатические процессы. Такие состояния и процессы в реальности не существуют.
2.2. Внутренняя энергия
Внутренняя энергия 
(Дж) – энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.п.) и энергия взаимодействия этих частиц.
В общем случае внутренняя энергия термодинамической системы включает следующие компоненты:
1) Кинетическая энергия теплового поступательного и вращательного движения молекул;
2) Кинетическая и потенциальная энергия колебаний атомов в молекулах;
3) Потенциальная энергия, обусловленная межмолекулярными взаимодействиями;
4) Энергия электронных оболочек атомов и ионов;
5) Кинетическая и потенциальная энергия взаимодействия нуклонов в ядрах атомов.
В нашем курсе рассматриваем первый и третий компоненты.
Внутренняя энергия – однозначная функция состояния термодинамической системы, т.е. в каждом состоянии система обладает определённой внутренней энергией (она не зависит от того, как система пришла в данное состояние). При переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода: 
.
Внутренняя энергия идеального газа
Так как в идеальном газе потенциальная энергия связи между молекулами пренебрежительно мала по сравнению с кинетической энергией их движения, то, исходя из закона равномерного распределения молекул, получим: 
, где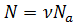 
– число молекул газа; 
– кинетическая энергия теплового хаотического поступательного и вращательного движения молекул. С учётом этого получаем: 
. Так как 
– универсальная газовая постоянная, то окончательно получим выражение для внутренней энергии идеального газа:
.
В случае одного моля идеального газа (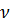
= 1 моль): 
.
Внутренняя энергия моля идеального газа зависит только от его абсолютной температуры.
