Особенность этого вида выборки заключается в том, что предварительно генеральная совокупность по признаку типизации разбивается на частные группы (типы, районы), а затем в пределах этих групп производится выборка.
Предельная ошибка средней при типическом повторном отборе определяется по формуле:
, (6.16)
а при типическом бесповторном отборе по формуле:
, (6.17)
где 
- средняя из внутригрупповых дисперсий (
) по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности средняя из внутригрупповых дисперсий определяется по формуле:
, (6.18)
где ni – численности единиц совокупности по каждой группе.
Границы (пределы) средней по генеральной совокупности на основе данных типической выборки определяются по тому же неравенству, что и при собственно-случайной выборке. Только предварительно необходимо вычислить общую выборочную среднюю 
из частных выборочных средних 
. Для случая пропорционального отбора это определяется по формуле:
, (6.19)
При непропорциональном отборе средняя из внутригрупповых дисперсий исчисляется по формуле:
, (6.20)
где Ni – численности единиц групп по генеральной совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
, (6.21)
Предельная ошибка доли признака при типическом повторном отборе определяется по формуле:
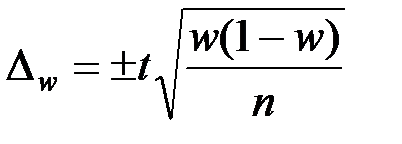, (6.22)
а при типическом бесповторном отборе по формуле:
.
Средняя дисперсия доли признака из групповых дисперсий доли wi(1-wi) при типической пропорциональной выборке исчисляется:
, (6.23)
Средняя доля признака по выборке из показателей групповых долей рассчитывается по формуле:
, (6.24)
Средняя дисперсия доли при непропорциональном типическом отборе определяется по формуле:
, (6.25)
а средняя доля признака:
, (6.26)
Серийная выборка
Серийная ошибка выборки может применяться в двух вариантах: а) объём серий различный и б) все серии имеют одинаковое число единиц (равновеликие серии). Наиболее распространённой в практике статистических исследований является серийная выборка с равновеликими сериями. Генеральная совокупность делится на одинаковые по объёму группы-серии (R) и производится отбор не единиц совокупности, а серий (r). Группы (серии) для обследования отбирают в случайном порядке или путём механической выборки как повторным, так и бесповторным способом. Внутри каждой отобранной серии осуществляется сплошное наблюдение. Предельные ошибки выборки (∆) при серийном отборе исчисляются по формулам:
а) при повторном отборе
, (6.27)
б) при бесповторном отборе
, (6.28)
где R – число серий в генеральной совокупности; r – число отобранных серий; 
– межсерийная дисперсия, исчисляемая для случая равновеликих серий по формуле:
, (6.29)
где 
– среднее значение признака в каждой из отобранных серий;
– межсерийная средняя, исчисляемая для случая равновеликих серий по формуле:
, (6.30)
